Министерство труда, занятости и социальной защиты РТ

Государственное автономное образовательное учреждение

среднего профессионального образования

«Колледж малого бизнеса и предпринимательства»

Методические указания

по математике

для заочного отделения

специальности 260807 «Технология продукции общественного питания»

Разработала: преподаватель

Корнеева Наталья Сергеевна

Казань 2012

Содержание

1. Введение

2. Общие рекомендации

   1. Чтение учебника

   2. Решение задач

   3. Самопроверка.

3. Правила выполнения и оформления контрольных работ

4. Программа и методические указания к контрольной работе по темам:

   1. Последовательности

   2. Функция, предел функции

   3. Производные и дифференциалы

   4. Численное интегрирование

5. Задания для контрольной работы

6. Литература

Введение

В настоящее время математические методы широко используются для решения самых разнообразных задач науки, техники и экономики. Значение этих методов существенно выросло в связи с массовым применением во всех отраслях электронно- вычислительных машин.

Математика является фундаментальной дисциплиной. Цель ее преподавания в учреждении среднего профессионального образования предусматривает:

- развить логическое мышление и повысить общий уровень математической культуры;

- познакомить студентов с математическим аппаратом. Необходимым для изучения общенаучных дисциплин;

- выработать у студентов умение самостоятельно изучать учебную литературу по математике и ее приложениям;

- выработать навыки к математическому исследованию прикладных задач .

Общие рекомендации

студенту-заочнику по работе над курсом математики

Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебнику, решение задач. Самопроверка. Выполнение контрольных работ. Во время сессий студенты слушают лекции, посещают практические занятия. Сдают устные зачеты и экзамены. При самостоятельном изучении учебного материала можно использовать следующие рекомендации.

1 . Чтение учебника

1. Каждый следующий вопрос должен изучаться только после правильного понимания предыдущего .

2. Особое внимание следует обращать на определение основных понятий. Их следует знать точно, а также подробно разбирать примеры, которые поясняют такие определения и уметь строить аналогичные примеры самостоятельно.

3. При изучении материала по учебнику полезно вести конспект, в который рекомендуется вписывать определения, формулировки теорем, уравнения и т.д. На полях конспекта необходимо отмечать вопросы, на которые необходимо получение устной или письменной консультации преподавателя.

4. Выводы, полученные в виде формул, рекомендуется подчеркивать или обводить рамкой, чтобы при перечитывании они выделялись и лучше запоминались. Полезно составить лист, содержащий важнейшие и наиболее часто употребляемые формулы курса. Такой лист поможет запомнить эти формулы , а также послужит постоянным справочником.

2. Решение задач

1. Чтение учебника должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь.

2. Решение задач и примеров следует излагать подробно, обосновывая каждый этап решения теоретическими положениями курса. Чертежи можно выполнять от руки, но аккуратно и в соответствии с данными условиями.

3. В промежуточных вычислениях не следует вводить приближенные значения корней, чисел π,e и т.п. Следует обратить внимание. Соответствует ли ответ существу данной задачи.

3.Самопроверка

При изучении математики большое значение имеет проверка правильности понимания, усвоения и выполнения задания. Необходимо научиться самопроверке. При этом приемы самоконтроля могут быть различные:

- проверка правильности усвоения материала путем сравнения своих формулировок с данными в учебнике ( если свои записаны);

- проверка результатов решения задачи по готовому ответу, а еще лучше по готовому решению, когда сразу видно, в каких местах есть пробелы;

- проверка результатов решения по аналогичному решению;

- проверка результата с помощью обратных действий.

Требования к выполнению и оформлению письменной контрольной работы

При выполнении контрольной работы необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.

1. Контрольная работа выполняется в школьной тетради в клетку чернилами любого цвета, кроме красного. Следует пронумеровать страницы и оставить на них поля 4-5 см для замечаний преподавателя.

2. На обложке тетради должен быть приклеен титульный лист утвержденного образца или аккуратно записаны все данные титульного листа: шифр; фамилия, имя, отчество студента ; предмет и номер работы. Здесь же следует указать название учебного заведения, дату отсылки работы и адрес студента. В конце работы следует проставить дату ее выполнения и расписаться.

3. В работу должны быть включены все задачи, указанные в задании строго по положенному варианту. Контрольные работы, содержащие не все задачи задания , а также задачи не своего варианта, не зачитываются.

4. Решение задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номера задач данной методички.

5. Перед решением каждой задачи надо полностью выписать ее условие.

6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу и делая необходимые чертежи.

7. Если сданная на проверку работа не зачтена, то обязательно выполняется работа над ошибками. Работа над ошибками делается в той же тетради, где записана не зачтенная контрольная работ, после рецензии преподавателя и повторно сдается на проверку. Если в тетради закончились чистые листы, то в тетрадь вставляется новая и прошивается вместе с основной тетрадью.

8. Выполненная работа сдается методисту СПО до начала сессии.

Теория к контрольной работе

Последовательности

Пусть задан занумерованный бесконечный набор чисел х_1,х_2,…,х_{n,… .} Это значит, что всякому натуральному числу n=1,2,… поставлено в соответствие по определенному закону число х_n.

Определение: Всякий занумерованный бесконечный набор чисел х_1,х_2,…,х_n,… называется числовой последовательностью.

Пример: 1) Последовательность всех четных натуральных чисел

2,4,6,….2n,…

2) Последовательность всех квадратов натуральных чисел

1,4,9,16,…n²,…

Обозначают: х_n, n=1,2,… или

Х_n называется общим членом последовательности.

Способы задания последовательностей

1. Чаще всего последовательность задают формулой общего члена.

Пример: х_n= , n=1,2,…

2. Рекуррентный способ, когда в явном виде задаются один или несколько первых членов последовательности и указывается формула, которая позволяет выразить последующие члены через предыдущие.

Пример : х₁=х₂=1, х_n=x_n-1+x_n-2

3. Последовательность может быть задана словесно.

Пример: последовательность простых чисел

2,3,5,7,11,13,17,19,23,… (т.е. можно указать саму последовательность, но для нее нет общего члена)

Определение: последовательность называется монотонно возрастающей, если для любого n выполняется неравенство х_n<х_n-1, т.е. каждый следующий член больше предыдущего.

Определение: Числовая последовательность называется ограниченной, если найдется число ε>0 такое, что дл всех номеров n=1,2,…выполняется равенство .

Определение: Числовая последовательность называется неограниченной, если какое бы большое число ε>0 ни взять, всегда найдется номер n такой, что .

Определение: Неограниченная последовательность, для которой неравенство выполняется сплошь для всех n, больших некорого номера, зависящего от ε, называются бесконечно большими (б.б.), т.е.

Пример:

Определение: числовая последовательность называется бесконечно малой(б.м.), если

Предел последовательности

Рассмотрим последовательность х_n= , n=1,2,…

:1, … ,т.е. члены этой последовательности с увеличением номера приближаются к нулю. Если рассмотреть другую последовательность, то там может быть другое число, к которому приближаются члены последовательности.

Определение: Число А называется пределом последовательности х_n, n=1,2…, если разность α_n=х_n-А является б.м. последовательностью.

Обозначается предел символом

Замечание: предел постоянной равен самой постоянной.

Последовательности, имеющие предел, называются сходящимися; в противном случае последовательность называется расходящейся.

Теорема 1:Если последовательность имеет предел, то он единственный.

Заметим , что из определения можно сделать вывод, что б.м. последовательности – это те и только те, предел которых равен нулю, т.е. сказать , что х_n,n=1,2… - б.м. и - одно и то же.

Свойства сходящихся последовательностей

Теорема 2:Пусть х_n и у_n ,n=1,2,… - сходящиеся последовательности, т.е. lim x_n=a, limy_n=b.

Тогда справедливы следующие утверждения:

1. для любого числа М последовательность Мх_n тоже сходится, причем 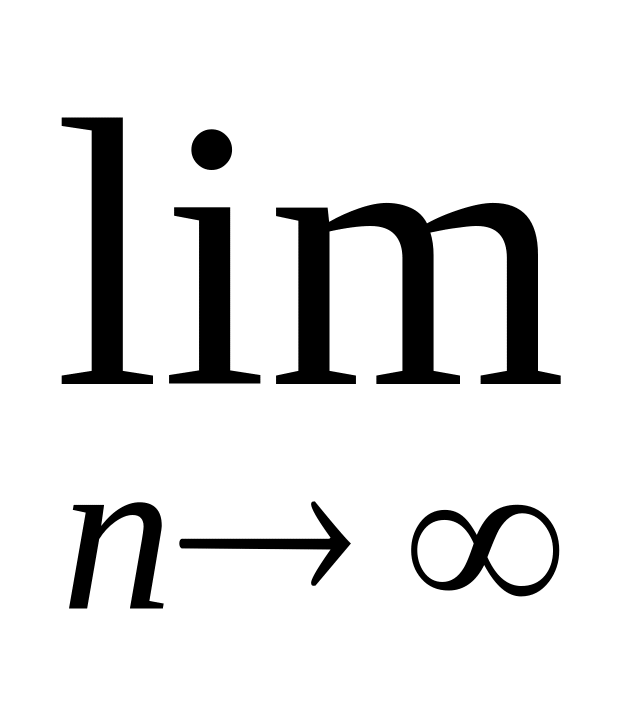(Mx_n)=M x_n=Ma;

2. сумма (разность) х_n и у_n также сходится, причем (x_n 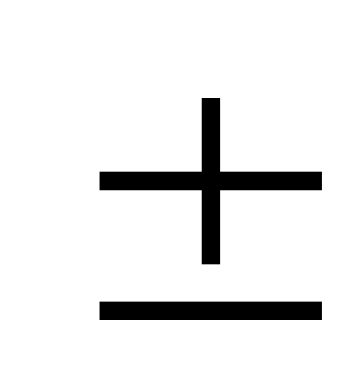y_n)=a b;

3. произведение х_ny_nтакже сходится, причем (x_ny_n)=ab;

4. при условии, что b 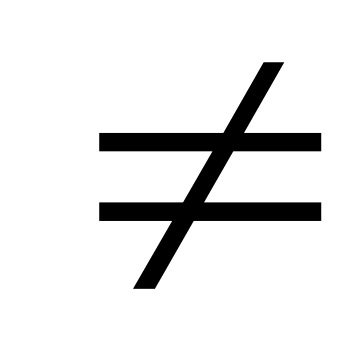0 частное также сходится, причем =

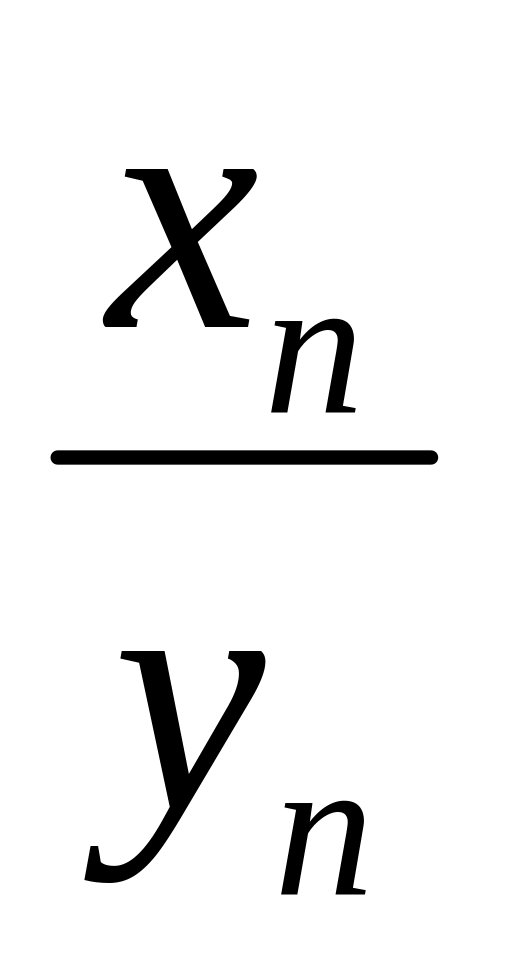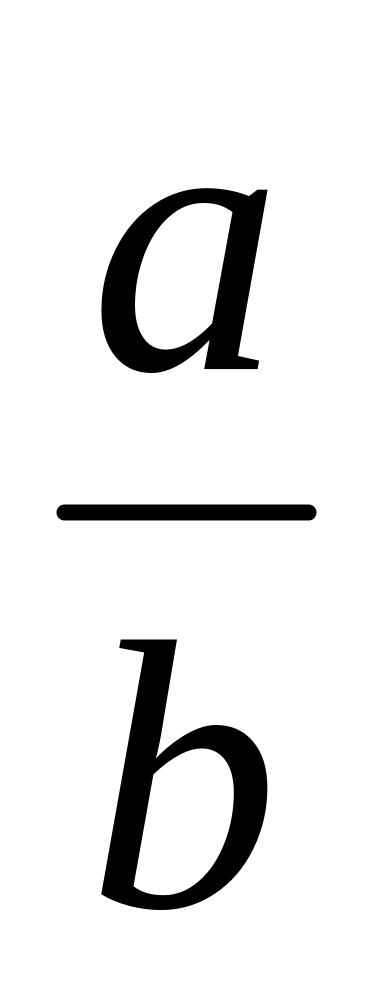
пример :Найти предел .

=(утверждение 1)= = = ( )=(утверждение 2)= ( 1- - )= (1-0-0)=

В рассмотренном примере непосредственное (т.е. без предварительных преобразований) использование теоремы 2 невозможно, т.к.это приводит к виду . Выражение данного вида называют неопределенностью вида . Аналогично определяются неопределенности вида . Раскрытие этих неопределенностей и составляет содержание практики нахождения пределов.

Монотонные последовательности. Число e.

Теорема: всякая монотонная и ограниченная последовательность сходится (т.е. имеет конечный предел).

Последовательность х_n= монотонно возрастает и ограничена сверху числом М=3 и предел этой последовательности по определению равен e, т.е. e.

Данный предел носит название второго замечательного предела и используется для раскрытия неопределенности вида (1 ).

Функция. Предел функции.

Пусть Х и У – некоторые множества и каждому элементу х Х поставлено в соответствие по некоторому правилу у У. говорят , что задана функция у=f(x) на множестве Х со значениями во множестве У.

х – аргумент функции

Х – область определения

У- область значений.

Если Х и У-множество действительных чисел, то говорят о числовой функции. примерами числовых функций являются линейная (у=ах+b), тригонометрическая (у=cos x),…

Функции могут быть заданы с помощью формул, таблиц, словесно и т.д.

Рассмотрим поведение функции при условии, что х стремится к числу а (х а)

Определение: число b называется пределом функции у=f(x) при х а, если для любой последовательности аргументов х₁,х₂,…х_n,…( х_n а), сходящейся к а, соответствующая последовательность значений функции у(х₁), у(х₂),…у(х_n),… сходится к b.

Обозначается:

Пример:

Основные теоремы о функциях, имеющих предел, аналогичны теоремам для сходящихся последовательностей.

неопределенности и способы их раскрытия для функций определяются аналогично последовательностям.

Замечательные пределы функции

Для вычисления пределов функций и раскрытия неопределенностей используют 2 замечательных предела и их следствия, которые отразим в следующей таблице.

Таблица замечательных пределов

1. первый замечательный предел	7.
2.	8.
3.	9. , где α-вещественный параметр
4.	10.
5.	11. -второй замечательный предел
6.	12.

Пример: Найти предел

= x²+ =0+ =2 =2

При решении использовалось свойство для вычисления предела суммы двух функций и первый замечательный предел.

Бесконечно малые функции. Метод эквивалентных бесконечно малых величин.

Определение: Функция α(х) называется бесконечно малой при х , если она имеет предел, причем этот предел равен нулю, т.е. α(х)=0.

Бесконечно малые функции могут стремиться к нулю по-разному или. как говорят, с разной скоростью. Поэтому их принято сравнивать между собой в зависимости от того , как ведет себя их отношение.

Пусть α(х) и β(х) – две бесконечно малые (б.м.) функции при х .

Определение: Б.м. α(х) и β(х) называют б.м. одного порядка малости, если существует предел , причем А 0.

Пример:

Получаем, что б.м. функции х² и 1-cosx имеют один порядок малости.

Определение: Две б.м. функции α(х) и β(х) называются эквивалентными при х , если предел их отношения равен 1, т.е. .

Примерами эквивалентных б.м. функций являются пары функций, приводящие к замечательным пределам (см.таблицу) .

Эквивалентность б.м. обозначается символом ~

Таблица эквивалентных величин (при х )

1. sinx~x	6. ln(1+x)~x
2. arcsinx~x	7. ax~x·lna, a 1,a>0
3.tgx~x	8. loga(1+x)~x/lna, a 1,a>0
4.arctgx~x	9. (1+x)α-1~αx,α R
5. ex-1~x	10. 1-cosx~x2/2

Практическое значение таблицы определяется следующей теоремой

Теорема: Пусть α(х) ~ α₁(х), β(х) ~ β₁(х) и существует . Тогда существует и предел , причем = .

Пример: Найти предел

Т.к. sin2x~2х при х , то = =0+2=2

Непрерывность функции

Пусть функция у=f(х) определена в некоторой окрестности точки а, включая саму точку а.

Определение: Функция у=f(х) называется непрерывной в точке а, если:

1) она определена в точке а;

2) существует

3) .

Если хотя бы одно из условий не выполняется, то говорят, что функция у=f(x) имеет разрыв в точке а, а сама точка а называется точкой разрыва.

Обозначим х-х₀ = у-у₀= у. тогда определение непрерывности можно сформулировать по-другому: функция называется непрерывной а точке х, если из условия следует, что и у .

Утверждение: Все элементарные функции непрерывны в каждой точке своей области определения.

Свойства непрерывных функций

Пусть функции f(x) и y(x) непрерывны в точке а, с-любое число. Тогда функции сf(x), f(x)±y(x), f(x)·y(x), (y(x)≠0) также непрерывны.

Свойства непрерывных функций отражают 2 теоремы. Известные как теоремы Вейерштрасса.

Определение: Функция у=f(х) , определенная на отрезке , называется ограниченной на этом отрезке, если найдется число М>0 такое, что для любого х выполняется неравенство .

Первая теорема Вейерштрасса: Если функция f(x) непрерывна на отрезке , то она ограничена на этом отрезке.

Определение: Значение f(x₀), где х₀ , называется наибольшим значением функции на отрезке, если для любой точки х справедливо неравенство f(x)≤f(x₀).

Максимальное значение функции в точке обозначают , а саму точку – х_max

Аналогично определяется минимальное значение функции в точке.

Вторая теорема Вейерштрасса: Если функция f(x) непрерывна на отрезке , то она принимает на этом отрезке как свое максимальное , так и свое минимальное значение.

Дифференциальное исчисление функции одной переменной

Разность х-х₀ называется приращением аргумента и обозначается т.е. =х-х₀, тогда близкая к х₀ точка х=х₀+ .

Приращением функции у=f(х) в точке х₀ называется разность у=f(х₀+ )-f(x₀).

Если существует предел отношения у к приращению в этой точке, когда приращение аргумента стремится к нулю, то этот предел называется производной функции в точке х₀ и обозначается у^/(х₀).

Производную функции можно обозначать символами: у^/, , .

Операция нахождения производной функции называется дифференцированием функции.

Из равенства dy – дифференциал функции.

С геометрической точки зрения производная – это угловой коэффициент касательной к графику функции в данной точке.

С физической точки зрения производная – это скорость изменения функции по отношению к изменению аргумента.

Определение : Если у=f(u) есть функция аргумента u, u=u(x) есть функция аргумента х, то y=f(u(x)) есть сложная функция от х.

Производная сложной функции вычисляется по формуле