9. Абсолютная и условная сходимость интегралА

2-го рода и критерий коши

1. Определение 5. Несобственный интеграл называется абсолютно сходящимся, если сходится и условно сходящимся, если сходится, а расходится.

Теорема 9 (признак Дирихле). сходится, если а) f (x) непрерывна и имеет ограниченную первообразную на [a, b); б) g(x) на [a, b) непрерывно дифференцируема и монотонна и .

Пример 51. Исследовать на абсолютную и условную сходимость . Решение. Используем признак Дирихле. Возьмем непрерывную на [1, 1), а . и первообразные .Тогда первообразная для f(x), очевидно ограничена на [0, 1) и g(x) непрерывно дифференцируема, а g’(x) = -1 < 0, т.е. g(x) монотонно убывает (здесь взяли g’(x) и проверим ее знак, чтобы так поступать в общем случае) и . Таким образом, оба условия признака Дирихле выполнены и искомый интеграл сходится.

Проверим абсолютную сходимость. На [0, 1) верно неравенство . Но - расходится (что будет доказано в примере 53 по критерию Коши). Тогда по мажорантному признаку для положительных функций расходится и значит исходный интеграл сходится, но не абсолютно.

Замечание 12. При доказательстве абсолютной сходимости можно использовать признаки сходимости для положительных функций.

Теорема 10 (признак Абеля). Интеграл сходится, если

1) f(x) непрерывна на [a, b) и сходится; 2) g(x) ограничена, непрерывно дифференцируема и монотонна на [a, b).

Пример 52. Исследовать на абсолютную и условную. сходимость . Решение. Воспользуемся признаком Абеля. Введем функции и . Очевидно сходится, а g(x) будет ограничена: и (здесь использован подход через произвольную для установления монотонности). Тогда g(x) убывает на [0, π). Отсюда по признаку Абеля получаем сходимость исходного интеграла. Возьмем модуль от подинтегральной функции. Очевидно на [0, π) . Но сходится. Отсюда по мажорантному признаку для положительных функций получаем сходимость и тем самым абсолютную сходимость исходного интеграла. Теорема 11. Если интеграл 2-го рода абсолютно сходится, то он также и сходится.

Таким образом, можно начинать проверку сходимости с абсолютной, ибо если она имеется, то получаем и сходимость интеграла.

Замечание 13. Все вышеприведенные признаки изложенные для отрезка [a, b) очевидным образом переносятся на отрезок (a, b]. Если же имеется на отрезке несколько особых точек, то применяем признаки по каждому отрезку отдельно.

2. Здесь рассмотрим критерий Коши интеграла 2-го рода.

Теорема 12 (критерий Коши). Пусть f(x) определена на [a, b) и интегрируема в собственном смысле на любом и неограничена в левой окрестности точки x = b. Тогда для сходимости необходимо и достаточно, чтобы для любого числа существовало такое число , что для любых : .

В доказательстве расходимости критерий формулируется так: расходится, если существует число , что для любого числа существуют , для которых .

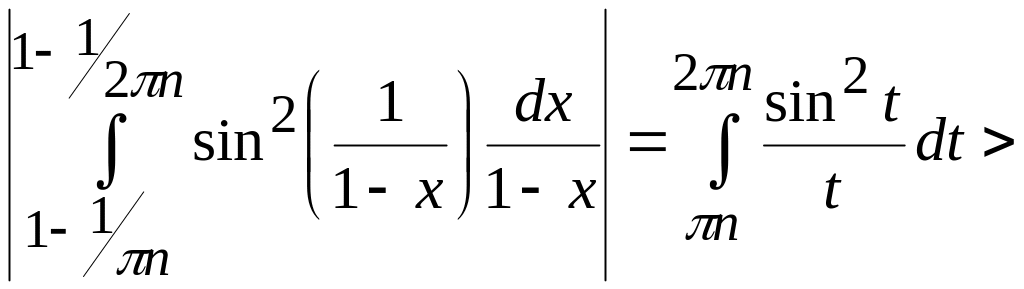
Пример 53. Доказать расходимость . Решение. Возьмем любое число и натуральное n, такое, что . Оценим интеграл по отрезку . Сделаем замену . Тогда . При для любого существуют , , такие, что . Согласно критерию Коши (вернее его отрицанию) получаем расходимость исходного интеграла.