4. Критерий коши и признаки сходимости несобственного интеграла 1-го рода

1. Теорема 3 (критерий Коши). Интеграл сходится тогда и только тогда, когда для любого ε > 0 существует такое, что при всех с , d > Δ выполнено неравенство , где f(x) интегрируема на любом отрезке из [a, ∞). .

Замечание 6. Критерий Коши удобно использовать для доказательства расходимости Так расходится, если существует число такое, что для всех существуют с > Δ и d > Δ такие, что . Рассмотрим примеры на критерий Коши.

Пример 22. Используя критерий Коши, исследовать на сходимость интеграл . Решение. Пусть некоторые числа c, d > 1. Тогда . Здесь для определенности взяли 1 < c < d..Тогда при . Возьмем . Очевидно и при c, d > Δ из неравенства (С) получаем для любого ε > 0: . Тем самым выполнен критерий Коши и исходный интеграл сходится.

Пример 23. Исследовать по критерию Коши для . Решение. Возьмем любое и выберем натуральное число n так, чтобы и положим и . Тогда и, с учетом x^-α (2πn)^-1, получаем .. . Итак существует , что при всех существуют , с при . Тогда исходный интеграл расходится.

2. Определение 2. Интеграл называется абсолютно сходящимся, если сходится и условно сходящимся, если сходится, а расходится.

Теорема 4. Абсолютно сходящийся интеграл будет и сходящимся.

Замечание 7. Для исследования абсолютной сходимости можно применять все достаточные признаки (мажорантный, предельный) для положительных подинтегральных функций.

Пример 24. Исследовать на абсолютную и условную сходимость . Решение. Рассмотрим . Так как и сходится, то по мажорантному признаку сходится - интеграл от модуля подинтегральной функции. Тогда исходный интеграл будет абсолютно сходится, а по теореме 4 он будет и сходящимся.

Пример 25. Исследовать на абсолютную и условную сходимость .Решение. Используем здесь формулу интегрирования по частям. Положим и . Тогда , а и . Таким образом, исходный интеграл сходится или расходится в зависимости от сходимости интеграла . Но сходится абсолютно, так как по признаку сравнения (мажорантному) и сходится. Следовательно, - сходится по теореме 4, а с ним и . Покажем, однако, что сходится условно. Рассмотрим . Из неравенства имеем . Тогда, если расходится, то по мажорантному признаку расходится и . Но расходится (см. пример 23 при α = 1). Таким образом, здесь нет абсолютной сходимости, а только условная для .

Приведем, теперь, достаточные условия сходимости интеграла 1-го рода, которые иногда называют еще признаками условной сходимости. .

Теорема 5 (признак Дирихле). сходится, если: а) f(x) непрерывна и ее первообразная ограничена на [a, ∞); б) g(x) непрерывно дифференцируема и монотонна на [a, ∞) и .

Пример 26 (на признак Дирихле). Исследовать на абсолютную и условную сходимость при всех числах α. Решение. Пусть α > 1. Тогда из очевидного неравенства и сходимости по мажорантному признаку (теорема 1) имеем сходимость и, тем самым, абсолютную сходимость исходного интеграла при α > 1.

Пусть . Положим f(x) = sinx, а . Проверим выполнение условий теоремы 5 (признака Дирихле). Условие а) здесь выполнено, так как sinx непрерывна на [1, ∞), а ее первообразная F(x) = - cosx будет ограничена на [1, ∞) ибо |F(x)| = |-cos x| 1. Условие б) здесь тоже выполнено, так как на [1, ∞) и, следовательно, g(x) убывает, а . Тогда по признаку Дирихле сходится. Но абсолютно же исходный интеграл не сходится, поскольку на [1, ∞) и на основе примера 23 при (а здесь ) расходится и по мажорантному признаку для положительных функций расходится и здесь нет абсолютной сходимости, а только условная для . Пусть . Покажем по критерию Коши расходимость . Возьмем число Δ > 1 и подберем натуральные n так, чтобы . Положим и . Тогда на [c, d]

, а и . Отсюда имеется такое, что для любого Δ>1 существуют

числа >Δ и >Δ, для которых . Поэтому при интеграл расходится.

Теорема 6 (признак Абеля). Интеграл сходится, если: а) f(x) непрерывна на [a, ∞) и сходится; б) g(x) ограничена, непрерывно дифференцируема и монотонна на [a, ∞).

Пример 27 (на признак Абеля). Исследовать на сходимость . Решение. Пусть α > 0. для и g(x) = arctg x. Условие а) признака Абеля выполнено, так как непрерывна на [1, ∞) и при α > 0 интеграл сходится (см. пример 26) и б) выполняется, так как . Тогда g(x) монотонна, так как возрастает, а и по признаку Абеля интеграл сходится для α > 0 .

. Пусть . Тогда аналогично предыдущему примеру 26 можно показать расходимость для , используя критерий Коши. Действительно, для всех n с 2πn > Δ , где Δ > 1 существуют числа и . Тогда на [c, d] функции , , а . Тогда . Беря , получаем, что по критерию Коши интеграл расходится. Рассуждения здесь в применении критерия Коши такие же, как в примере 26.

Если же , то из неравенства и сходимости при получаем сходимость - или абсолютную сходимость исходного интеграла для всех .

Пусть теперь . Воспользуемся здесь признаком Дирихле и Абеля одновременно. Представим , где , а . По доказанному в примере 26 интеграл при сходится, а функция ограничена, на [1,∞) и . Тем самым функция q(x) монотонно (возрастает). Тогда по признаку Абеля будет сходиться. Абсолютно же интеграл при не сходится, так как из оценки на [1, ∞) и расходимости при (на основе примера 23) будет расходиться Отсюда мажорантному признаку для положительных функций получаем расходимость или отсутствие абсолютной сходимости для . Итак, исходный интеграл сходится для , абсолютно для , условно и расходится для .

Приведем метод выделения главной части, основаный на утверждении, что если подинтегральная функция f(x)=g(x)+R(x), где R(x) абсолютно интегрируемая, то f(x) и g(x) одновременно либо абсолютно интегрируемы, либо условно интегрируемы, либо не интегрируемы при .

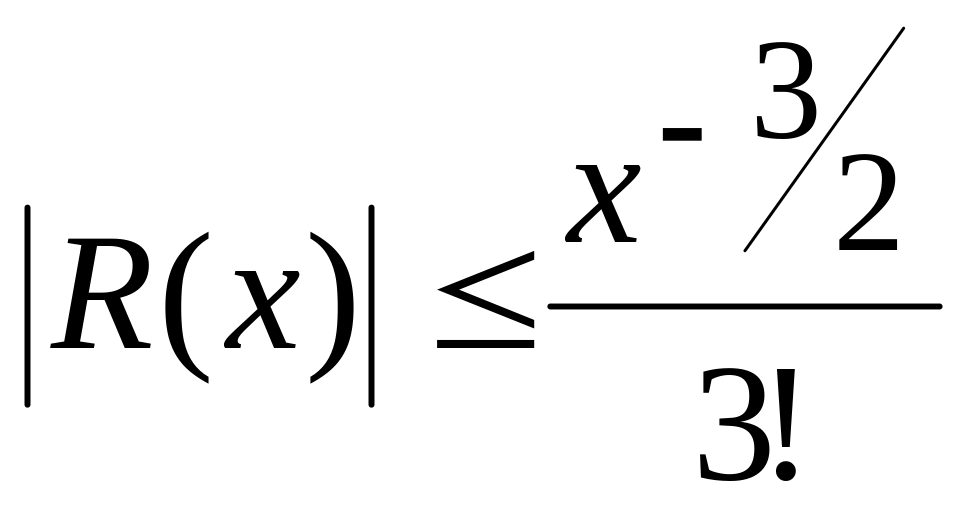Пример 28. Исследовать на абсолютную и условную сходимость. Решение. Так как при функция , то используя разложение по формуле Тейлора , где ее остаток и . Тогда , где . Но абсолютно сходится по мажорантному признаку, так как сходится . Но сходится условно (пример 26) при . Отсюда исходный интеграл сходится условно по методу выделения главной части.

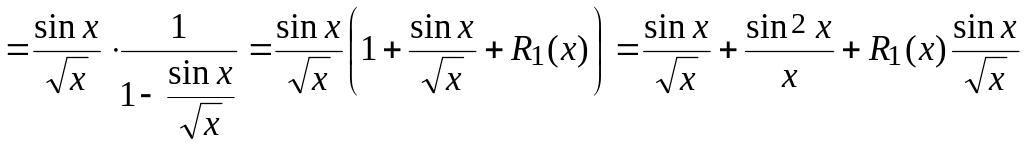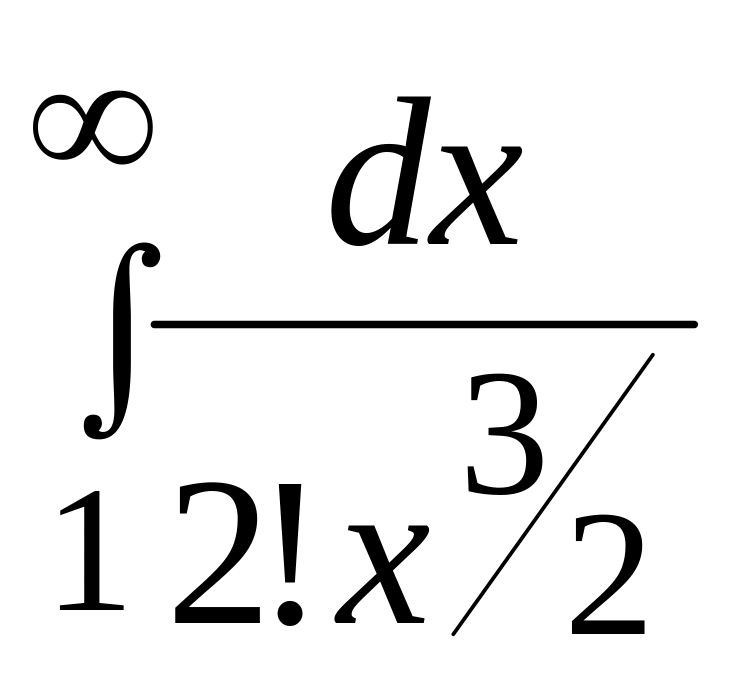Пример 29. Исследовать интеграл на абсолютную и условную сходимость. Решение. Представим функцию . Здесь использовано разложение в окрестности 0 на основе формулы Тейлора , где . Вводя , получаем оценку . Но сходится по мажорантному признаку, ибо сходится. Отсюда абсолютно сходится и вид сходимости исходного интеграла по методу выделения главной части определяется сходимостью . Но этот интеграл расходится, так как расходится (пример 23 при α = 1), а сходится (пример 26 при ). Тогда исходный интеграл расходится.