8

3. Передатні функції динамічних систем

3.1. Операційне числення

Ще однією формою вхід-вихідного опису динамічної системи (елементів) є передатна функція. Цей спосіб опису динамічних систем базується на методах операційного числення, під якими розуміється сукупність методів прикладного математичного аналізу, що дозволяють економними і такими, що безпосередньо ведуть до мети засобами отримувати рішення лінійних диференціальних рівнянь, різницевих і деяких інтегральних рівнянь.

Суть операційного методу полягає в наступному.

Нехай задана деяка функція f(t) дійсної змінної t причому така, що для неї існує перетворення Лапласа (L-перетворення)

.

Використовуючи L-перетворення, можна кожній перетворюваній по Лапласу функції поставити у відповідність іншу функцію F(s) комплексної змінної s. При цьому функцію f(t) прийнято називати функцією-оригіналом, або просто оригіналом, а функцію F(s) — функцією-зображенням, або просто зображенням. Перетворення Лапласа дозволяє використовувати ряд його дуже зручних для практики властивостей. Наприклад, диференціюванню оригіналу f(t) по змінній t відповідає операція множення зображення F(s) на комплексну змінну s, а інтегрування оригіналу f(t) за змінною t відповідає операція ділення зображення F(s) на змінну p. Таким чином, операції диференціювання і інтегрування оригіналу замінюються в просторі зображень простішими алгебраїчними операціями множення і ділення на s. Це дозволяє диференціальне рівняння системи замінити в просторі зображень на алгебраїчне рівняння відносно зображень. Розв’язавши це алгебраїчне рівняння відносно зображення F(s), ми можемо отримати зображення розв’язку початкового диференціального рівняння. Для визначення самого розв’язку можна скористатися зворотним перетворенням Лапласа

, , де

Таким чином, метод розв’язування диференціального рівняння за допомогою операційного числення зводиться до схеми, представленої на рис. 3.1

Рис. 3.1. Узагальнена схема розв’язку задач за допомогою перетворення Лапласа

Слід зазначити, що у багатьох випадках при знаходженні розв’язку f(t) можна уникнути безпосереднього обчислення інтеграла зворотного перетворення Лапласа, скориставшись таблицею відповідностей "оригінал - зображення" і властивостями перетворення Лапласа.

3.2. Перетворення Лапласа і його властивості

Як вже відзначалося, суть перетворення Лапласа полягає в тому, що деякій функції f(t) дійсної змінної t ставиться у відповідність інша функція F(s) комплексної змінної s за умови, що існує (сходиться) інтегральне перетворення:

(3.1)

f(t) - називається функцією-оригіналом (чи просто оригіналом).

F(s) - називається функцією-зображенням (чи просто зображенням).

Для того, щоб функція f(t) була оригіналом і мала функцію зображення, необхідно і достатньо виконання наступних умов :

1. функція f(t) неперервна для усіх t>0, за винятком, можливо, скінченного числа точок розриву I роду

2. функція f(t)=0 для усіх значень t<0

3. функція f(t) має обмежений порядок зростання, тобто можна вказати такі постійні числа М>0 і С₀>О, для яких виконується умова при .

Багато функцій, що зустрічаються при описі процесів в динамічних системах, є оригіналами. Наприклад, оригіналами є 1(t), Asinωt*1(t), tⁿ1(t), e^a1(t), (a>0) і ряд інших. Наявність в цих функціях множника – одиничній ступінчастій функції – забезпечує виконання другої умови. Фізична інтерпретація цього полягає в тому, що цікавляться деяким процесом, починаючи з деякого моменту часу t₀. Саме у момент часу t₀ передбачається початок деякої дії на систему. Часто в лінійних системах вважають t₀=0.

Якщо хоч би одна з умов 1-3 не виконується, то функція f(t) не буде оригіналом. Таким чином, перетворення (3.1) є перетвореннями Лапласа і умовно позначаються

або .

Існує і зворотне перетворення Лапласа, яке дозволяє по відомій функції, - зображенню визначити відповідну функцію оригіналу:

.

Властивості перетворення Лапласа. Приведемо без доказів коротке зведення властивостей перетворення Лапласа. Детальний виклад цих властивостей можна побачити в спеціальній літературі.

Тут і далі вважатимемо, що , і так далі, а також виконані усі інші умови математичного характеру. Усі властивості, що приводяться тут, можна довести, використовуючи перетворення (8.1) безпосередньо.

4. Лінійність перетворення

, , де .

5. Диференціювання і інтегрування оригіналу

, де ,

узагальнюючи

,

де – деяка постійна величина.

і т.д.

6. Зміщення в області оригіналів і в області зображень

, .

7. Зміна масштабу

, а – дійсне додатнє число.

8. Множення в комплексній і дійсній областях

, .

9. Диференціювання і інтегрування зображення

, .

10. Початкове і граничне значення оригіналу

, .

11. Перетворення періодичної функції-оригіналу f(t)

,

де Т- період функції f(t), F(s) – зображення (протягом одного періоду).

12. Похідна по параметру.

Нехай f(t,a) - функція-оригінал, перетворювана по Лапласу відносно змінної t, F(s,a) - її функція-зображення, a - параметр, не залежний від t і s. Справедливі наступні співвідношення

, , .

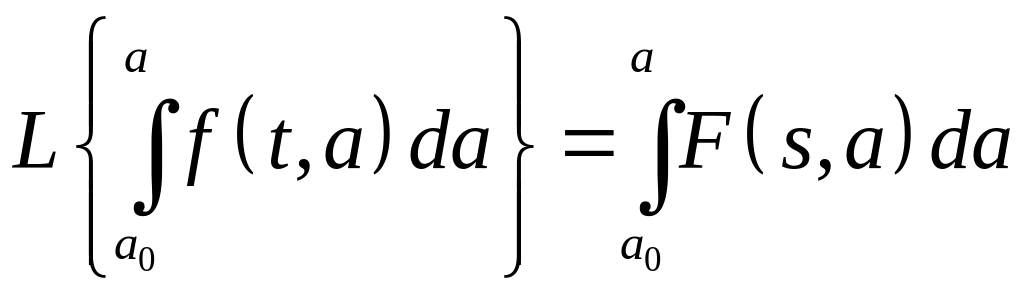З цих формул виходить, що співвідношення не порушиться, якщо в лівій і правій його частинах виконувати операції граничного переходу, диференціювання і інтегрування відносно параметра а.

На закінчення приведемо коротку таблицю відповідностей "оригінал - зображення", значно детальніші таблиці можна знайти в довідниках.

, , , , , , , , , , .

Перетворення Лапласа з урахуванням його властивостей і таблиця елементарних операцій дозволяють звести досить складні рішення диференціальних рівнянь до рощв’язування алгебраїчних рівнянь в зображеннях.

Приклад. Необхідно розв’язати диференціальне рівняння

з початковими умовами у(0) = 3, у'(0) = – 2.

Нехай Y(p)=L{у(t)}, тоді з урахуванням того, що і властивостей перетворення Лапласа, отримуємо рівняння відносно зображення Y(p):

Далі знайдемо

.

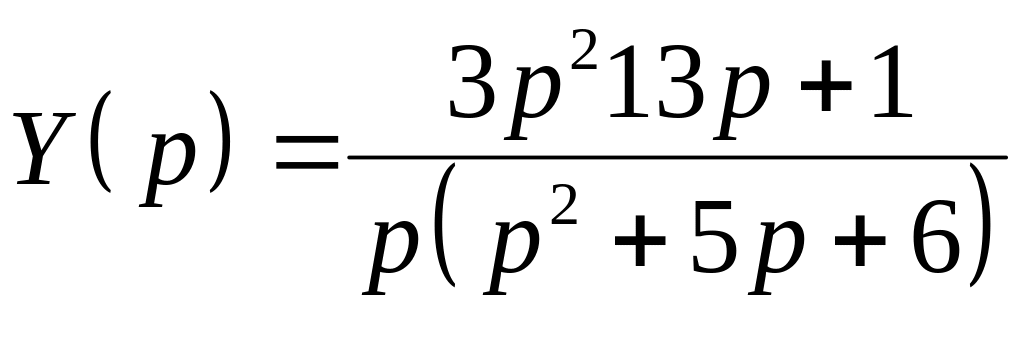Для знаходження оригіналу далі можна застосувати формулу зворотного перетворення Лапласа, яка приведе до обчислення розв’язку.

Використання властивостей перетворення Лапласа і таблиці відповідностей "оригінал - зображення" дозволяє отримати рішення легшим способом. Для цього представимо отриманий результат у вигляді суми елементарних дробів, скориставшись методом невизначених коефіцієнтів.

Нехай отримане зображення представлене у вигляді

,

де A, B, C — невідомі доки коефіцієнти, значення яких необхідно знайти.

Проведемо очевидні алгебраїчні перетворення дробу

Тоді очевидно, що коефіцієнти при однакових степенях p повинні дорівнювати:

Ця система алгебраїчних рівнянь має рішенням значення

.

Таким чином, отримане раніше зображення Y(p) може бути представлене у виді

,

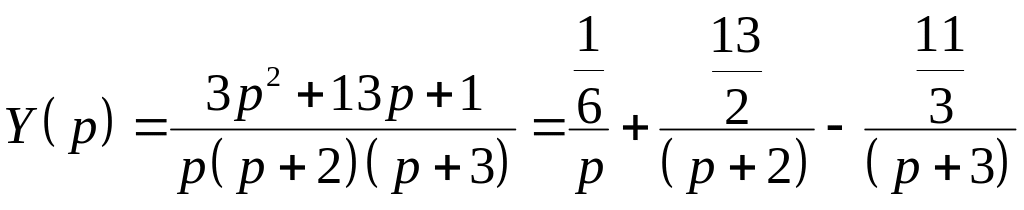Використовуючи властивості перетворення Лапласа і таблицю відповідностей, отримуємо

Остаточно шуканий розв’язок диференціального рівняння набуває вигляду

.

Розв’язування системи диференціальних (чи інтегро-диференціальних) рівнянь з постійними коефіцієнтами проводиться способом, аналогічним приведеному вище. Кожне з рівнянь, що входять в систему, перетвориться по Лапласу, а потім система алгебраїчних рівнянь, що вийшла, вирішується відносно розв’язку зображення. Оригінал визначається вказаними вище способами.