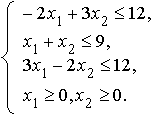3.2 Общая формулировка задачи линейного программирования

Линейное программирование - это математическая дисциплина, изучающая методы нахождения наименьшего (или наибольшего) значения линейной функции нескольких переменных, при условии, что последние удовлетворят конечному числу линейных уравнений или неравенств.

Общая математическая формулировка задачи линейного программирования выглядит следующим образом.

Среди неизвестных x₁ , x₂ ,… , x_n , удовлетворяющих системе

a ₁₁х₁ + а₁₂х₂ +…+ а_1nx_n ≥ b_1,

a₂₁x₁ + a₂₂x₂ +...+ a_2nx_n ≥ b_2,

............................................

a_m1x₁ + a_m2x₂ +...+ a_mnx_n ≥ b_m,

x₁ ≥ 0, x₂ ≥ 0,…, x_n ≥ 0,

определить такие, при которых функция F = c₁x₁ + c₂x₂ +...+c_nx_n  max (min), т.е. достигает своего наименьшего или наибольшего значения.

Все задачи линейного программирования можно разбить на два вида. Задачи, в которых требуется минимизировать целевую функцию - задачи минимизации. Задачи, в которых требуется максимизировать целевую функцию – задачи максимизации.

Любую задачу максимизации можно свести к задаче минимизации и наоборот.

3.3 Каноническая форма задачи линейного программирования

Задача ЛП, представленная в форме

F = c₁x₁ + c₂x₂ +...+c_nx_n  max

a ₁₁х₁ + а₁₂х₂ +…+ а_1nx_n = b_1,

a₂₁x₁ + a₂₂x₂ +...+ a_2nx_n = b_2,

............................................

a_m1x₁ + a_m2x₂ +...+ a_mnx_n = b_m,

x_j ≥ 0 (j=1,2,…,n)

Называется канонической формой задачи ЛП.

Переход от стандартной формы к канонической

Для осуществления данного перехода нужно в каждое из m неравенств системы ограничений ввести m дополнительных переменных s₁, s₂, …, s_m, тогда система ограничений примет вид:

a ₁₁х₁ + а₁₂х₂ +…+ а_1nx_n+ s₁ = b_1,

a₂₁x₁ + a₂₂x₂ +...+ a_2nx_n + s₂= b_2,

............................................

a_m1x₁ + a_m2x₂ +...+ a_mnx_n + s_m = b_m,

x_i ≥ 0, s_i ≥ 0 (i=1,2,…,m; j=1,2,…,n)

s₁, s₂, …, s_m – выравнивающие, балансовые переменные.

Если в стандартной форме требовалось минимизировать целевую функцию, то вводим

F₁=- F = -c₁x₁ - c₂x₂ -...- c_nx_n  max

Пример.

Пусть задача линейного программирования задана в стандартной форме:

F = 2х₁ + 3х₂  max

при ограничениях:

х₁+3х₂≤18

2 х₁+x₂≤16

х₂≤5

3х₁≤21

х₁0, х₂ 0

Приведем эту задачу к каноническому виду.

Обратим имеющуюся систему неравенств в равенства, вводя для этого в каждое из них соответствующую неотри­цательную переменную:

х₁+3х+ s₁=18

2 х₁+x₂ + s₂=16

х₂ + s₃ = 5

3х₁+ s₄ = 21

х_j0, s_i 0

В данном примере все переменные введены со знаком «+», так как рассматриываемые неравенства имеют знак ≤. Если бы неравенства имели знак , переменные нужно было бы вводить со знаком «-»

§4. Графический метод решения задач лп

Определение 6. Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит весь отрезок, соединяющий эти точки.

Рис а – выпуклое множество, б – не является выпуклым.

Теорема. Множество решений неравенства с двумя переменными является одной из двух полуплоскостей, на которые вся плоскость делится прямой , включая и эту прямую, а другая полуплоскость с той же прямой есть множество решений неравенства

Пример.

П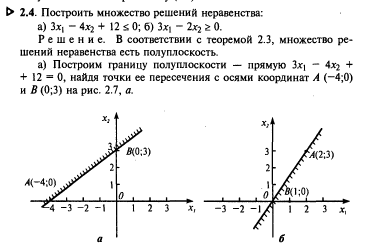 остроить множество решений неравенства 3х₁-4х₂+12≤0

Построим границу полуплоскости – прямую 3х₁-4х₂+12=0 по точкам А(-4;0), В(0;3).

Для определения искомой полуплоскости рекомендуется взять произвольную контрольную точку, не лежащую на границе и проверить выполнение неравенства. Если неравенство выполняется, то оно выполняется и во всех точках полуплоскости, содержащей контрольную точку и не выполняется во всех точках другой полуплоскости. В качестве контрольной точки удобно выбирать начало координат. Искомую полуплоскость выделяем штриховкой.

Теорема. Множество решений совместной системы m линейных неравенств с двумя переменными

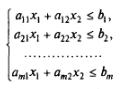
Является выпуклым многоугольником или выпуклой многоугольной областью.

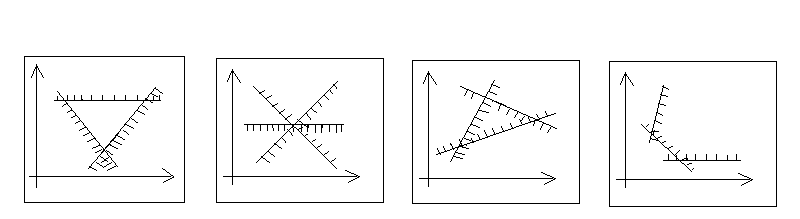
При построении областей решений систем неравенств возможны случаи:

1. Система ограничений несовместна – пустое множество

2. Система ограничений имеет единственное решение

3. Система ограничений имеет конечное число решений (имеется замкнутая область допустимых решений)

4. Система ограничений имеет бесчисленное множество решений

Р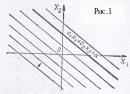 ассмотрим задачу ЛП в стандартной форме с двумя переменными. Т.к. система ограничений задачи ЛП есть система линейных неравенств, то множество ее решений есть выпуклый многоугольник М, лежащий в первой четверти координатной плоскости.

С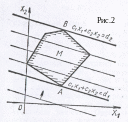 учетом этого задача формулируется следующим образом: среди всех точек выпуклого многоугольника найти такую, координаты которой минимизируют (максимизируют) линейную функцию F = с₁х₁ + с₂х₂

Если зафиксировать какое-нибудь значение функции F = d, то получим линейное уравнение с двумя неизвестными c₁x₁ + c₂x₂ = d, график которого есть прямая, перпендикулярная вектору , которая называется линией уровня. При изменении d от - ∞ до + ∞ прямая c₁x₁ + c₂x₂ = d, смещаясь параллельно самой себе, «зачертит» всю плоскость (рис.1).

П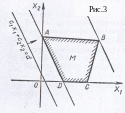 усть М – многоугольник решений системы ограничений (рис.2). При изменении d от - ∞ до + ∞ прямая c₁x₁ + c₂x₂ = d при некотором значении d = d₁ достигает многоугольника М и имеет с ним общую точку А (точка «входа»), а затем, пройдя весь многоугольник М, при некотором значении d = d₂ будет иметь с ним последнюю общую точку В (точка «выхода»).

Наименьшего значения целевая функция F = с₁х₁ + с₂х₂ достигает в точке «входа» А и наибольшего значения в точке «выхода» В.

Возможен случай, когда при перемещении прямой c₁x₁ + c₂x₂ = d «вход» («выход») прямой в многоугольник решений М произойдет по стороне этого многоугольника (рис, 3, 4). Это случится, если в многоугольнике М есть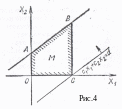 стороны, параллельные прямой c₁x₁ + c₂x₂ = d. В этом случае точек «входа» («выхода») бесчисленное множество, минимальное (максимальное) значение целевая функция принимает во всех точках этой стороны многоугольника.

Так, координаты всех точек отрезка AD (рис. 3) минимизируют значение функции F = с₁х₁ + с₂х₂ а координаты всех точек отрезка AB (рис. 4) максимизируют значение целевой функции.

В случае открытых областей прямая c₁x₁+c₂x₂ = d при изменении d от - ∞ до + ∞ не имеет точки «выхода» из области решений (рис. 5). Тогда максимальное значение функцией не достигается.

У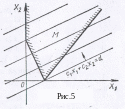 читывая, что оптимальное значение целевая функция принимает в точках «входа» и «выхода», то есть в вершинах области решений, существует следующий план графического решения задачи линейного программирования:

1. Построить математическую модель задачи.

2. На координатной плоскости построить множество допустимых решений.

3. Построить вектор

4. Построить линии уровня для целевой функции.

5. Параллельным переносом этой прямой в направлении вектора определить, какие из вершин многоугольника допустимых решений являются точками «входа» или «выхода» в зависимости от требования задачи.

6. Найти координаты точек «входа» («выхода»)

7. Вычислить оптимальное значение функции.

8. Провести интерпретацию полученного решения.

9. Уточнить математическую модель (если необходимо).

Пример

Пусть в результате экономического исследования была построена следующая задача, целевая функция определена и имеет вид , система ограничений