9.6. Затопленные турбулентные струи

В некоторых технических задачах (например, при проектировании устройств струйной гидропневмоавтоматики) при­ходится рассчитывать параметры турбулентных затопленных

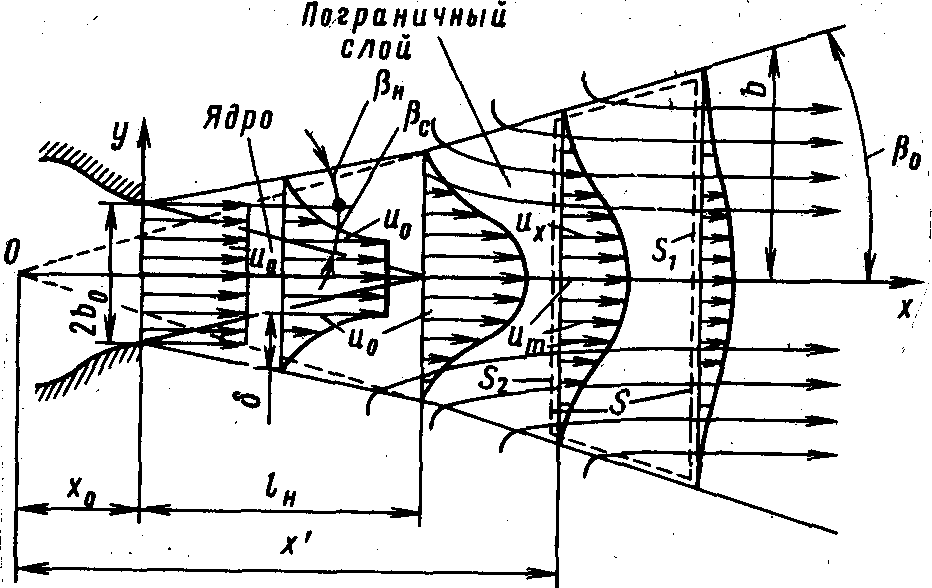
Рис. 9.7. Схема свободной турбулентной струи

струй, образующихся при истечениях жидкости из отверстий и сопл в среду тех же физических свойств, что и струя. Режим течения в таких струях может быть ламинарным, однако наибольшее практическое значение имеют турбулентные струи, основы теории которых рассмотрены в настоящем параграфе.

Дадим прежде всего качественное описание структуры затопленной свободной, т. е. не стесненной стенками, турбулентной струи, вытекающей из плоского или круглого сопла (рис. 9.7). Если сопло надлежащим образом профилировано, то распределение скоростей в его выходном сечении будет равномерным. По мере продвижения струи происходит ее торможение окружающей жидкостью и наряду с этим вовлечение последней в движение. Поэтому на некотором расстоянии l_н поперечное сечение ядра течения с равномерным распределением скоростей уменьшается до нуля, а вокруг него образуется струйный пограничный слой, в котором скорость асимптотически изменяется от значения u₀ до нуля при удалении от оси струи. Участок длиной l_н, состоящий из ядра и струйного пограничного слоя, называют начальным участком свободной струи. За сечением х = l_н лежит относительно небольшой переходный участок.

Обычно используют упрощенную схему, полагая длину переходного участка равной нулю и считая, что в сечении х = l_н , начинается основной участок, целиком состоящий из струйного пограничного слоя, в котором скорость изменяется от u_m, на оси до нуля на достаточном удалении от нее. Осевая скорость u_m на основном участке убывает от значения u₀ до нуля на бесконечности. На рис. 9.8 приведены профили скоростей для плоской струи, вытекающей из прямоугольного отверстия размером 0,03 X 0,65 м; каждая кривая на рисунке соответствует фиксированному расстоянию х от выходного отверстия. Можно видеть, что ядро с равномерным распределением скоростей исчезает уже на

расстоянии 0,2 м. На рис. 9.9 показан профиль скоростей на основном участке, построенный в безразмерных переменных u_x / u_m = f(y/y_0,5), где y_0,5 — расстояние от оси, на котором скорость равна половине максимальной.

Характерной особенностью, установленной теоретическим анализом и многочисленными опытами, является приближенная прямолинейность границы равномерного ядра турбулентной струи и ее внешней границы, проведенной как геометрическое место точек, в которых скорость составляет заданную (малую) часть скорости на оси (например, и = 0,01u_m). Углы наклона внешних границ к оси струи на начальном и основном участках несколько различаются. Проведя внешние границы основного участка и продолжив их внутрь сопла до пересечения, получаем характерную для данной струи точку 0, называемую полюсом (см. рис. 9.7).

Линии тока в области струйного течения имеют вид, показанный на рис. 9.7. Их наклон к оси струи очень мал, а значит, мала и поперечная составляющая u_y скорости.

Приведенная схема движения качественно воспроизводит структуру течения плоской струи, вытекающей из широкого щелевого отверстия, или течения в меридиональной плоскости круглой струи.

Экспериментальные данные, а также данные теоретического анализа позволяют заключить, что по мере удаления от выходного сечения сопла распределение скоростей и другие параметры все меньше зависят от условий истечения, а безразмерный профиль скорости приобретает универсальный характер. Поэтому с известным приближением, если нас интересует главным образом основной участок, можно реальную струю заменить струёй-источником, т. е. бесконечно тонкой струёй, вытекающей в направлении оси х из полюса 0. Теоретическое описание струи-источника значительно проще, чем описание струи конечной толщины:

Наряду с расчетом параметров струй, распространяющихся в покоящейся среде, приходится определять параметры струй в потоках, а также двух или нескольких взаимодействующих струй. Существенное практическое значение имеют полуограни-

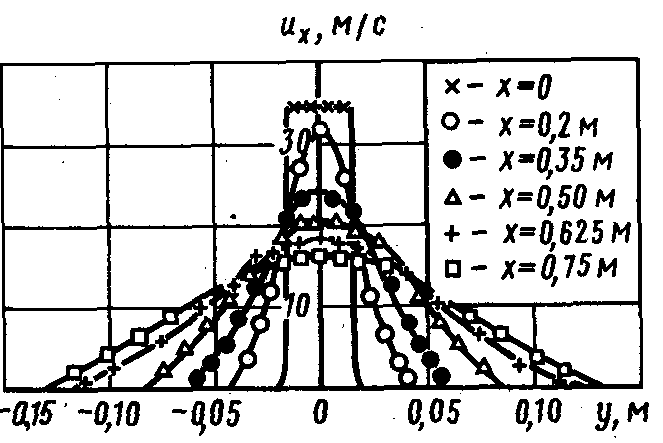
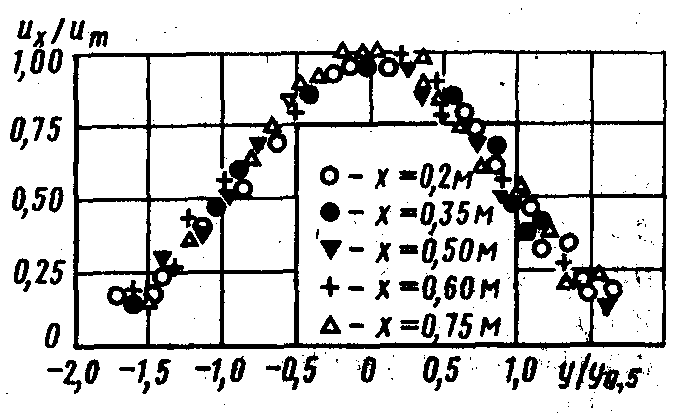
Рис. 9.8. Профиля скоростей плоской турбулентной струи

Рис. 9.9. Безразмерный профиль скорости на основном участке плоской турбулентной струи

ченные и ограниченные струи, с которыми приходится иметь дело при исследованиях потерь в местных сопротивлениях, при проектировании струйных элементов систем гидропневмоавтоматики, при расчетах проточных частей машин, аппаратов и т. п.

Рассмотрим закономерности и методы расчета некоторых простейших струйных течений.

Плоская свободная струя образуется при истечении из прямоугольного отверстия или сопла в достаточно большую емкость, стенки которой не влияют на параметры течения. Если пренебречь действием массовых сил, то в области такой струи давление, как показывает опыт, всюду можно считать постоянным (т. е. струя является изобарической). Поэтому уравнение количества движения, записанное для массы жидкости, ограниченной контрольной поверхностью S (штриховая линия на рис. 9.7), в проекции на ось х будет иметь вид

Это равенство выражает постоянство потока количества движения через любое поперечное сечение (обозначено индексами 1 и 2) свободной струи:

(9.30)

Значение постоянной легко определяется для начального 1 сечения

где 2b₀ — высота выходного отверстия; l₀—размер отверстия по нормали к плоскости течения.

Если ширину b струи определять с условной точностью, как указано выше, то

Вводя безразмерные величины u_x/u₀ и у/b, находим

Для отношения u_m/u₀ из этого уравнения получим

(9.31)

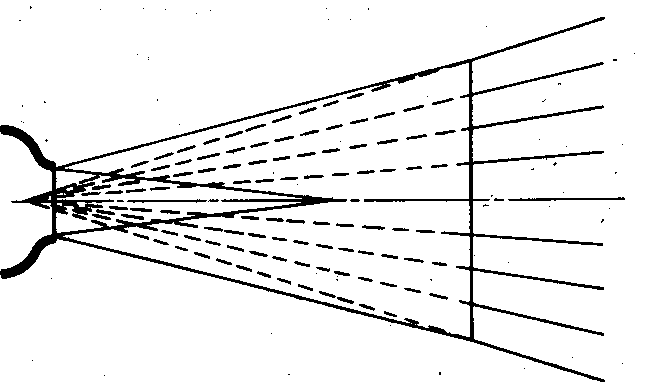
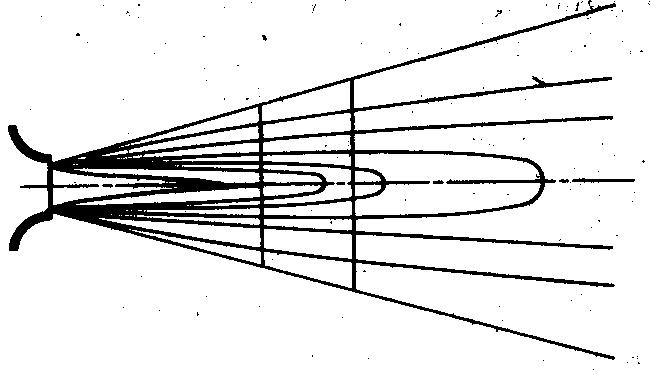
Рис. 9.10. Линии равных значений безразмерной скорости на основном участке затопленной струи

Рис. 9.11. Линии равных скоростей (изотахи) затопленной струи

Из рис. 9.9 следует, что безразмерный профиль скорости в пределах основного участка можно представить универсальной зависимостью

(9.32)

т. е. задача определения профиля продольной составляющей скорости на основном участке свободной струи является автомодельной.

Следовательно, интеграл, входящий в (9.31), равен некоторому числу, которое можно найти, если установлен закон (9.32) распределения скоростей. Равенство (9.31) можно записать как соотношение для определения скорости на оси струи

(9.33)

Если начало координат расположить в полюсе струи (см. рис. 9.7), то b = const х' и вместо выражения (9.33) можно записать

(9.34)

Таким образом, свободная плоская турбулентная струя неограниченно расширяется вниз по течению, а ее осевая скорость убывает обратно пропорционально корню квадратному из расстояния от полюса.

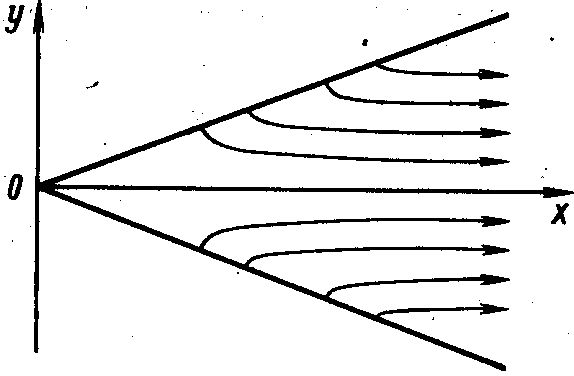
Из формулы (9.32) следует, что для основного участка линиями равных безразмерных скоростей u_x/u_m = const будут линии, для которых у/b = const. Поскольку b = constх', это эквивалентно условию у/х' = const. Иными словами, линии u_x/u_m = const образуют пучок прямых, проходящих через полюс струи (рис. 9.10). Линии и = const (изотахи) образуют факел (рис. 9.11).

Описанная кинематическая схема течения, хотя и является приближенной, но достаточно удовлетворительно подтверждается опытами.

Значения констант в формулах (9.33) и (9.34) определяются значением интеграла, входящего в уравнение (9.31). Для его вычисления необходимо найти форму профиля скорости в струйном пограничном слое. Эта задача имеет несколько полуэмпириче-

Рис. 9.12. Схема плоского турбулентного источника

ских решений, которые различаются как исходными предпосылками, так и формой результирующих зависимостей, но в большинстве своем удовлетворительно согласуются с результатами опытов.

Ниже приведено решение задачи о течении из плоского турбулентного источника (рис. 9.12), которое получено Гертлером на основе так называемой «новой теории свободной турбулентности Л. Прандтля». В силу сказанного выше это течение приближенно воспроизводит поток в области основного участка турбулентной струи. Начальная же часть источника между полюсом O и концом переходного участка должна быть исключена и заменена начальным и переходным участками струи, течение в которых требует специального рассмотрения.

Течение в области турбулентного плоского источника обладает всеми свойствами пограничного слоя и потому описывается уравнениями (9.3). Поскольку в струе dp/dx = 0, то и U dU/dx = 0. При этом уравнения (9.3) приобретают вид

(9.35)

В струйном пограничном слое _ < <_т, и потому в выражении (9.35) принимаем _ = _т. Преобразуем первое из этих уравнений. Если к его левой части прибавим величину u_x ди_y/ду + u_x ди_x/дх, которая в силу уравнения неразрывности равна нулю, то после очевидных преобразований получим

(9.36)

Согласно «новой теории Прандтля» примем, что кинематический коэффициент  турбулентной вязкости в формуле Буссинеска  =  ди_x/ду постоянен в пределах поперечного сечения струи. Приближенность этого допущения почти очевидна, так как вблизи границы струи (при больших у) более естественно считать   0. Тем не менее, результаты, получаемые при допущении о независимости  от у, оказываются вполне удовлетворительными. Принятая гипотеза и условия размерности позволяют заключить, что коэффициент в турбулентное вязкости можно выразить формулой

(9.37)

где = const.

Действительно, пусть  не зависит от у, т. е.  =  (х). Размерность в можно получить только путем умножения некоторой

характерной длины на характерную скорость. Выберем в качестве этих величии ширину струи b (х) и осевую скорость u_m(x); тогда формула (9.31) будет удовлетворять условию размерности и сформулированной гипотезе. Учтем, кроме того, b = кx и

u_m = nx^–1/2, где k и n — постоянные. Тогда

Принимая во внимание, что опытные данные достаточно точно подтверждают структуру формулы (9.32), будем искать профиль продольной составляющей скорости в виде

где — постоянная: F' — функция одной переменной  = y/х, подлежащая определению, причем штрих означает дифференцирование по той переменной.

Имея выражение для продольной составляющей скорости

и учитывая, что течение плоское, введем функцию тока , для которой

Находим

где g (х) — произвольная функция.

Граничные условия на оси струи-источника можно задать в виде  = 0 (у = 0); u_x = u_m ;  = 0. Следовательно, F (0) = 1 и n^–1 F (0) + g (х) = 0. Если выберем g (х) = 0, то получим F (0) = 0. Таким образом,

(9.38)

Вычислим теперь члены уравнения (9.36):

Подставляя эти выражения в уравнение (9.36) и производя упрощения, получаем уравнение для определения функции F:

которое можно представить также в виде

Отсюда следует, что

Постоянную C₁ определяем из условия на оси струи, т. е. при у= 0:

Следовательно, C₁ = 0. Для удобства интегрирования уравнения

учтем, что можно произвольно выбрать неопределенную пока постоянную . Допустим, что

в результате чего получим уравнение

интегрируя которое находим

Из граничных условий  = 0, F (0) = 0, F' (0) = 1 определяем С₂ = 1 и, следовательно,

В результате интегрирования этого уравнения при известных уже граничных условиях приходим к функциям

Согласно выражению (9.38) получаем распределение скоростей в поле струи-источника:

На основании опытных данных Рейхардта Гёртлер определил, что  = 7.67. На рис. 9.13 дано сопоставление профиля скорости, вычисленного по уравнениям (9.40), с опытными данными Рейхардта. Можно видеть, что в основной части профиля теория Гертлера дает неплохое совпадение с опытными данными, однако

Рис. 9.13. Сопоставление теоретического и экспериментального профилей скорости для основного участка плоской затопленной струн

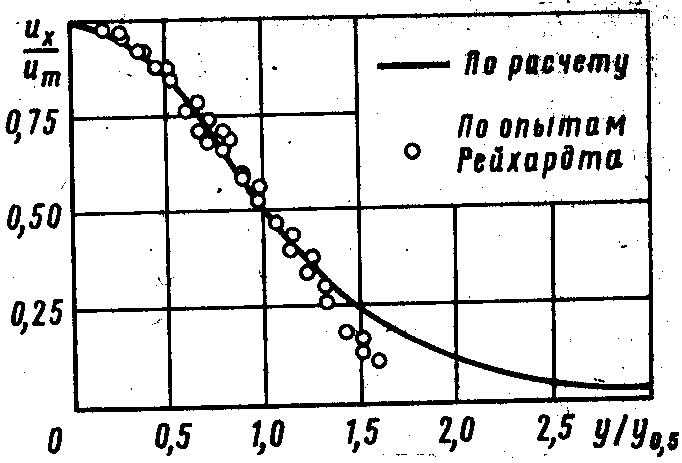
на границах струи в области малых скоростей теоретические скорости заметно больше опытных. Это расхождение можно объяснить приближенностью принятой в теории гипотезы о постоянстве коэффициента  в пределах поперечного сечения струи.

Наличие поперечной составляющей скорости на внешней границе струи приводит к подсасыванию (инжекции) жидкости в поле течения струи, благодаря чему ее расход возрастает вниз по течению.

Наряду с решением (9.42) существуют другие зависимости для описания поля скоростей плоской турбулентной струи. Весьма удобная формула для продольной составляющей скорости получается, если ее профиль аппроксимировать полиномом

Коэффициенты a_i можно найти из граничных условий:

при

при

Тогда закон распределения скорости примет вид

)

где  = y/b.

Хорошую согласованность с опытными данными дает также

формула

(9.42)

полученная Шлихтингом для распределения скорости в турбулентном следе за обтекаемым телом, но применимая и для струйного пограничного слоя.

Для начального участка плоской струи распределение скорости вне ядра течения, т. е. в струйном пограничном слое, можно получить и на основе уравнений (9.35). Для практических расчетов можно воспользоваться зависимостью Шлихтинга в форме

где

причем y_я представляет собой ординату границы ядра с равномерным распределением скорости (см. рис. 9.7), а  — толщина пограничного слоя:  = у_гр — у_я (здесь у_гр — ордината границы струи).

Использование полуэмпирических теорий, в том числе новой теории Прандтля, примененной выше для плоской струи, позволяет получить решение также и для осесимметричной струи-источника. Приведем основные данные о турбулентных плоских и осесимметричиых струях, необходимых для их практического расчета (подробное изложение см. в работах 15, 251). Все данные относятся к равномерному распределению скоростей на срезе сопла. Структура приводимых зависимостей обосновывается теорией, а значения постоянных определены на основе многочисленных опытов.

Плоская струя (см. рис. 9.7). Для определения скорости на оси струи в пределах основного участка служит равенство (9.31), которое можно переписать в виде

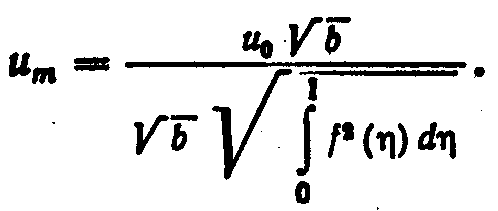
Поскольку b = tg ₀x' (где ₀ — угол наклона внешней границы струи к оси х),

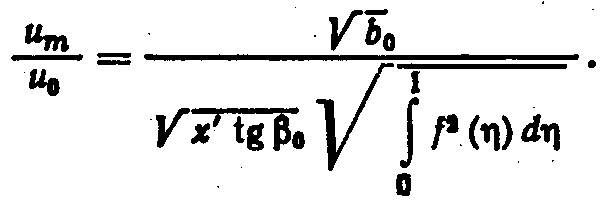
Если для функции f ()) использовать формулу (9.41), то

Согласно опытным данным, полученным Фертманом, tg ₀ = = 0,22. Тогда расчетная формула будет иметь вид

Для определения длины начального участка используем выражение (9.30), приравняв значения J в переходном сечении его значению на срезе сопла:

или

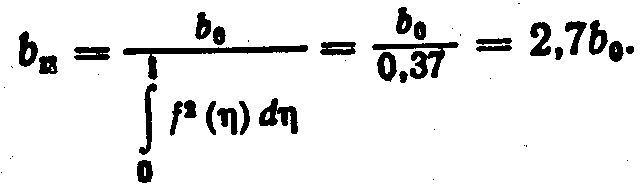
Теоретическое, подтверждаемое опытами, рассмотрение пограничного слоя в пределах начального участка показывает, что толщина  этого слоя увеличивается пропорционально расстоянию от среза сопла, т. е.  = с_нх, где для плоских и осесимметричных струй с_н = 0,27 (см. рис. 9.7). Следовательно, для конца начального участка, где b_п = _п = с_нx_н (индекс «п» означает, что параметры относятся к переходному сечению),

Зная x_п и b_п, можно вычислить угол _н расширения внешней границы на начальном участке и угол ее сужения ядра:

Установим закономерность изменения расхода плоской струи. Для начального участка

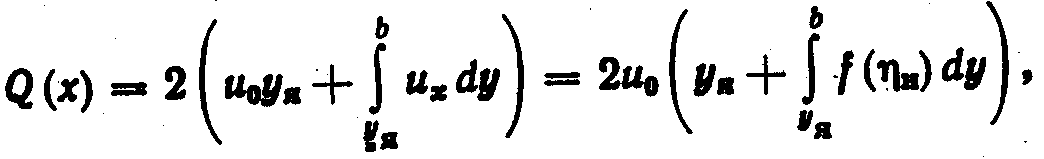
где _н=(y - y_я)/

Поскольку d = dy/,

Если использовать для функции f (_н) зависимость (9.41), то можно получить

Учитывая, что у_я = b₀ — х tg _с ,  = xc_н находим

Принимая tg _с = 0,1; с_н = 0,27 и разделив Q (х) на расход в выходном сечении сопла Q₀ = 2u₀b₀ получим безразмерную форму последней зависимости

(9.43)

где = х/b₀.

Расход на основном участке струи

или в безразмерном виде (9.44)

В переходном сечении формулы (9.43) и (9.44) должны давать один и тот же результат. Следовательно,

Так как = 10, то из последнего соотношения найдем полюс­ное расстояние = 2,3.

Таким образом определяют все геометрические параметры пло­ской затопленной струи.

Осесимметричная (круглая) струя. Ее расчет можно выполнить по аналогичной схеме. Основные результаты такого расчета следующие.

Закон изменения осевой скорости

толщина пограничного слоя в переходном сечении

длина начального участка, определяемая координатой

x_{п =}8,95b₀

Характерные углы

безразмерный расход на начальном участке

на основном участке

полюсное расстояние

Следует иметь в виду, что параметры турбулентной струи существенно зависят от равномерности распределения скоростей на срезе сопла, а также от степени турбулентности потока. При­веденные выше значения этих параметров относятся к малой турбулентности при равномерном распределении скорости и₀