
- •1.1. Введение.
- •1.2. Оптимизационные задачи в 2.
- •1.4. Понятие о nр-полноте.
- •Условие целочисленности решения задачи лп.
- •Критерий полной унимодулярности.
- •Задача о назначениях.
- •Задача коммивояжера.
- •2. Принятие решений и элементы теории игр.
- •2.1. Задачи многокритериальной оптимизации.
- •2.3. Игры.
- •Дележи.
- •3. Сетевые модели.
- •3.1. Способы задания графов.
- •3.2. Изоморфизм графов.
- •П оиск простейших узких мест графа за o(|e|).
- •3.3. Остовные деревья.
- •Описание алгоритма Прима:
- •Корректность алгоритма Прима.
- •3.4. Кратчайшие пути в графах. Волновой алгоритм построения дкп (Дейкстра)
- •Нахождение кратчайшего пути для ациклического орграфа
- •3.5. Потоковые задачи Задача о максимальном потоке (змп).
- •На входе: матрицы а –пропускных способностей, и c – цен, c ij 0 - стоимость пропуска единицы потока по ребру (I,j), f0 - ограничение на величину потока.
- •3.6. Приближенное решение np-полных задач.
- •Задача о максимальной клике.
- •3.7. Точные методы решения np-полных задач.
- •4. Элементы теории массового обслуживания.
- •4.1. Пуассоновский поток событий
- •4.2. Моделирование простейшего потока.
- •4.3. Процессы гибели и размножения.
- •Классификация систем массового обслуживания:
- •4.4. Открытая система м | м | 1 (один врач).
- •4.5. Замкнутые системы с резервированием. Будем различать горячий и холодный резервы, т.Е. Исправные, но включенные или выключенные приборы.
- •4.6. Задачи проектирования сетей технического обслуживания.
- •3.5. Алгоритм Тарьяна (для планарных графов мод строится за o(n)).
3. Сетевые модели.
Граф G–
это пара (V, E),
где V- конечное множество
помеченных вершин, а E V V
- множество ребер. Если ребра
( v1 , v2 )
и ( v2 , v1 )
различают, то граф называют ориентированным
(или орграфом), а его ребра ‑
дугами. Граф полный, если все
пары вершины соединены ребрами (число
ребер
![]() );
граф планарный, если его можно
нарисовать на плоскости без пересечения
ребер (число ребер планарного графа по
теореме Эйлера не превосходит 3∙(n-1)).
);
граф планарный, если его можно
нарисовать на плоскости без пересечения
ребер (число ребер планарного графа по
теореме Эйлера не превосходит 3∙(n-1)).
К лассификация
ребер орграфа.
1) Ребра дерева
поиска
(черные).
лассификация
ребер орграфа.
1) Ребра дерева
поиска
(черные).
2) Обратные (Back) ребра соединяют вершину с предком + петли.
3) Прямые (Forward) ребра соединяют вершину с потомком, не входя в дерево.
4) Перекрестные (Cross) ребра – все остальные.
3.1. Способы задания графов.
Графический: вершины изображаются точками, а ребра – линиями между ними.
матрица смежности A = {aij} |
|
матрица инцидентности B = {bij} |
||
aij = 1 ( v1 , v2 ) E |
граф неориентирован, a ij = a ji , т.е. матрица симметрична |
|
граф ориентирован,
|
|
Матричный: n = | V |, m = | E |.
Матрица смежности – лучший способ задания графов, близких к полным. Если граф планарен, то в каждой строке матрицы стоит в среднем ≈6 единиц. Выгоднее указать список всех ребер или список подсписков смежных вершин = {(номер вершины, {номера смежных вершин})},затрачивая log 2 n бит на номер.
Ex: n = 1000. Матрица смежности занимает 1000 1000 = 1000000 бит, список ребер ‑ 3 1000 20 = 60000 бит (10 бит на номер, 20 на ребро).
Т.к. граф определяется своей матрицей смежности, то существует 2 n n различных графов (= матриц смежности = наборов из n2 нулей и единиц)!!!
Граф называется графом без
петель, если в нем нет ребер вида
( vi , vi ),
т.е. на диагонали матрицы стоят нули.
Число таких графов равно 2 n (n-1).
Число неориентированных графов без
петель равно
![]() n (n-1)
(матрица симметрична).
n (n-1)
(матрица симметрична).
Путь –
последовательность ребер вида
![]() ,
т.е. конец предыдущего ребра, является
началом следующего ребра. Цикл –
это путь, у которого начало первого
ребра совпадает с концом последнего,
т.е. ik
= i1.
,
т.е. конец предыдущего ребра, является
началом следующего ребра. Цикл –
это путь, у которого начало первого
ребра совпадает с концом последнего,
т.е. ik
= i1.
Возведем в квадрат матрицу смежности. Что будет её элементами?
A = {aij {0,1}},
A 2 = {bij},
причем
![]() .
= числу таких k, при
которых aik = 1
и akj = 1,т.е.
есть ребра (i, k)
и (k, j),
.
= числу таких k, при
которых aik = 1
и akj = 1,т.е.
есть ребра (i, k)
и (k, j),
![]() есть
путь длины 2 из i в j.
есть
путь длины 2 из i в j.
Т.о. bij есть число различных путей длины 2 из i-й вершины в j-ую. A k- число путей длины k из i в j, причем пути могут не быть простыми (= без циклов).
Граф связный, если между любыми двумя вершинами есть путь.
Дерево – связный граф без циклов = связный граф, содержащий n-1 ребро.
Сколько различных деревьев существует на n вершинах?
Степень вершины i – это число единиц в i–ой строке матрицы смежности.
№17. Алгоритм кодирования деревьев.
Степени вершин S |
3 |
1 |
1 |
4 |
1 |
1 |
1 |
3 |
1 |
Номер вершины I (внизу - шага) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Отцовская вершина О |
1 |
4 |
1 |
4 |
8 |
4 |
8 |
9 |
|
Удаляемая вершина U |
2 |
3 |
5 |
1 |
6 |
7 |
4 |
8 |
9 |
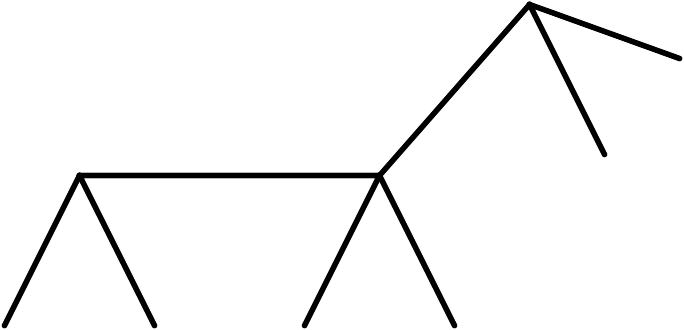

усть есть дерево.
На k-м шаге выбираем в векторе степеней S самую левую вершину Uk с единичной степенью, удаляем ее, а у нее и ее отца Ok уменьшаем степень на 1.
На основе вектора S и картинки мы построим 2 вектора U и О (вместо картинки можно использовать матрицу смежности). Размерности векторов U и O = n-1. По построению пара (Ui, Oi) является ребром дерева. Все Uk – различны (удалить вершину можно только 1 раз), но в векторе U не хватает вершины 9, ее мы перекинем из O, и получим вектор O*: dim(O*)=n-2; и вектор U*: dim(U*)=n. Зная O*, легко восстановить дерево. В самом деле, пусть N(i,A) - кратность числа i в векторе A. Очевидно, N(i,U*)=1 для всех i. Восстанавливаем S: Si = N(i,O) + N(i,U) = N(i,O *) + N(i,U *) = N(i,O *) + 1. Зная S, вычислим U1 1-е удаленное ребро графа = (U1, O1). Уменьшив на 1 степени вершин U1 и O1, найдем U2 и 2-е ребро графа (U2, O2) и т.д. Получили алгоритм декодирования. Рисовать восстанавливаемые ребра удобно в порядке, обратном удалению!
Соответствие между O* и деревом – взаимнооднозначное (докажите), число деревьев с помеченными вершинами = числу различных векторов O* = nn-2.
Напомним, что число неориентированных графов на n вершинах ‑2 n (n-1)/2.
Пример: Если n=3 и матрицу смежности неориентированного графа превратить в вектор из 0 и 1, то деревьям соответствуют 3 вектора из 8-ми: 110, 101 и 011.

Если n=4, то 42=16 деревьев из 26=64 неориентированных графов без петель.
Если n=5, то 53=125 деревьев из 210=1024 графов
Два графа называются изоморфными, если существует нумерация вершин второго графа, при которой матрицы смежности обоих графов совпадут.
Трудоемкость проверки изоморфности перебором нумераций равна O( n 2 n!).
Теорема. Графы изоморфны наборы степеней вершин у них совпадают.
Сколько различных неизоморфных деревьев можно построить на n вершинах?
n
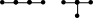
 =3
(1 дерево): n=5 (3
дерева):
=3
(1 дерево): n=5 (3
дерева):
n=4 (2 дерева):
Пусть Si – степень вершин, R – количество ребер дерева Si = 2*R = 2*(n-1). Выпишем упорядоченные по убыванию вектора степеней вершин при n=4:
2 2 1 1 и 2 1 1 1. Они различны, графы неизоморфны. Si =2*3 = 6.
Сколько различных упорядоченных векторов степеней вершин?
Есть n мест. На них нужно разместить 2(n-1) единиц (не менее одной на место).
n=5, n-2 = 3 |
n=6, 2(n-1)=10, n-2 = 4 |
3 0 0 0 0 2 1 0 0 0 1 1 1 0 0 сначала размещаем n-2 единицы |
4 3 1 0 0 0 0 | 4 2 1 1 1 1 - 2 2 2 0 0 0 0 | 3 3 1 1 1 1 - 3 2 1 1 0 0 0 | 3 2 2 1 1 1 - 4 1 1 1 1 0 0 | 2 2 2 2 1 1 - 5 п |
Нарисуем эти деревья. Четвертому вектору соответствуют два неизоморфных дерева!!! В одном из них соседями единственной вершины степени 3 являются 2 висячих вершины и одна со степенью 2, а во второй – наоборот.

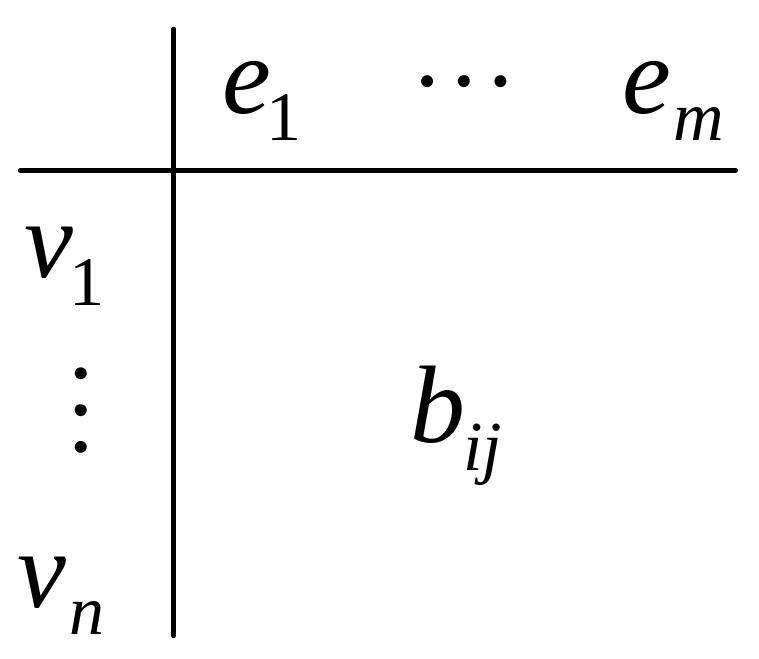
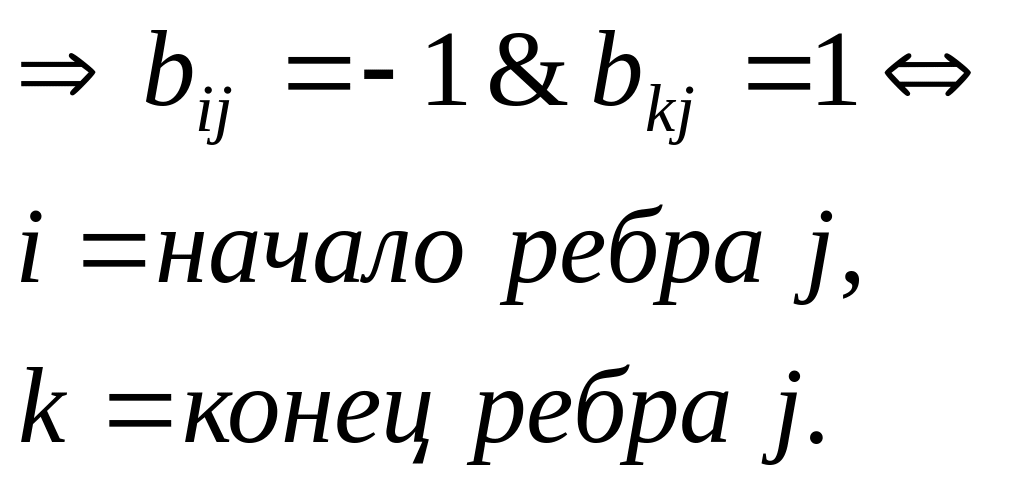
 0 0 0 0 0 | 5 1 1 1 1 1 - 1
0 0 0 0 0 | 5 1 1 1 1 1 - 1

 отом
- в каждую лунку добавим 1
отом
- в каждую лунку добавим 1