Условие целочисленности решения задачи лп.

Для того, чтобы x было целочисленным можно потребовать, чтобы все были целыми. Для этого достаточно, чтобы был равен 1. - это n равенств, которые выбираются способами из m неравенств.

Квадратная целочисленная матрица A называется унимодулярной, если ее определитель равен 1 или 0. Матрица размера , где называется вполне унимодулярной, если все ее определители n-го порядка равны 1 или 0.

Критерий полной унимодулярности.

Матрица размерности m×n, m≥n, состоящая из элементов 0, 1, -1, является вполне унимодулярной, если в каждом столбце содержится не более 2-х ненулевых элементов, а строки можно так разбить на 2 подмножества, что для каждого столбца с двумя ненулевыми элементами оба элемента лежат в одном подмножестве тогда и только тогда, когда эти элементы имеют разные знаки.

Доказательство проводится индукцией по размерности матриц.

Пусть для некоторого k критерий выполняется. Проверим его для k+1.

1. Существует столбец из нулевых элементов  определитель = 0.

2. Существует столбец с одним ненулевым элементом  определитель k+1-го порядка = 1 (-1)*(определитель k-го порядка)= 1.

3. Столбец имеет два ненулевых элемента. ???

Линейная комбинация строк равна 0  определитель = 0. ■

Задача о назначениях.

Есть n работников и n работ. Если i-й работник будет выполнять j-ю работу, то будет достигнута некоторая полезность c_ij. Как назначить работников на работы, чтобы суммарная полезность была максимальной? Пусть =1, если i-й работник выполняет j-ю работу, и 0, если нет. При этом: и

1. Каждый работник может выполнять только одну работу, т.е. i .

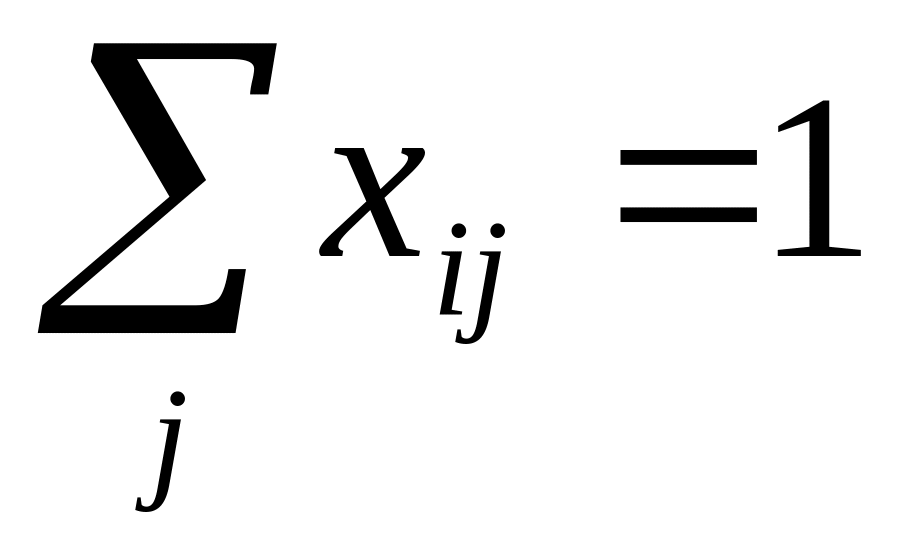2. Каждая работа выполнялась только одним работником, т.е. j .

Снимем условие целочисленности и запишем ограничения 1-2 в виде::

x₁₁+x₂₁+…+x_n1 =1 x₁₁+x₁₂+…+x_1n =1

… и … ,

x_1n+x_2n+…+x_nn =1 x_n1+x_n2+…+x_nn =1

В матричной форме Ax = 1, где (x_{11 …} x_1n x₂₁ … x_2n­ ... x_n1 ... x_nn),

а матрица A имеет вид:

1	…	0	1	…	0	…	1	…	0
0	E	0	0	E	0	…	0	E	0
0	…	1	0	…	1	…	0	…	1
1	…	1	0	…	0	…	0	…	0
0	…	0	1	…	1	…	0	…	0
0	…	0	0	…	0	…	1	…	1

В этой матрице в каждом столбце ровно два ненулевых элемента  матрица вполне унимодулярна и  квадратная подматрица имеет определитель 0, -1 или 1.  Решение ЛП с такой матрицей будет заведомо целочисленным  ЗН – полиномиально разрешима. Заметим, что более эффективным для ЗН является венгерский алгоритм, имеющий трудоемкость O(n³).