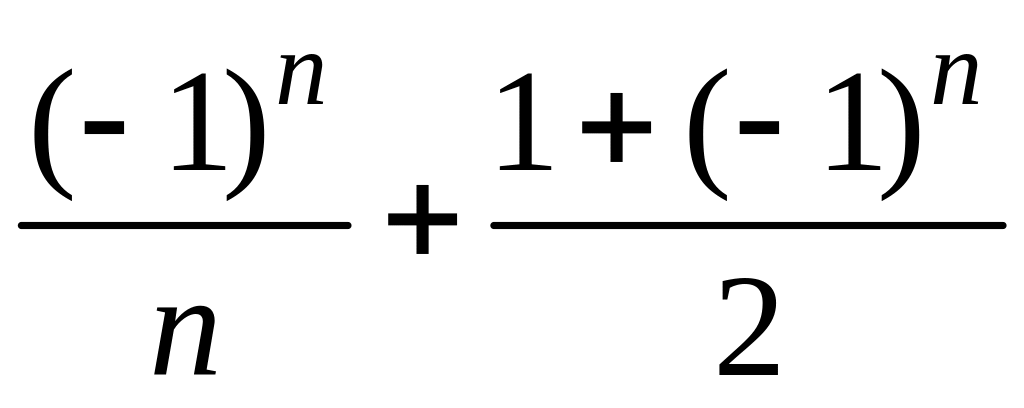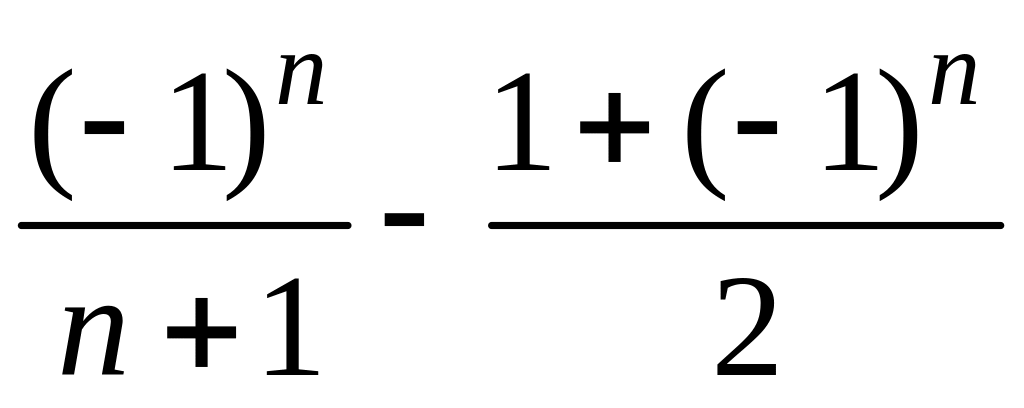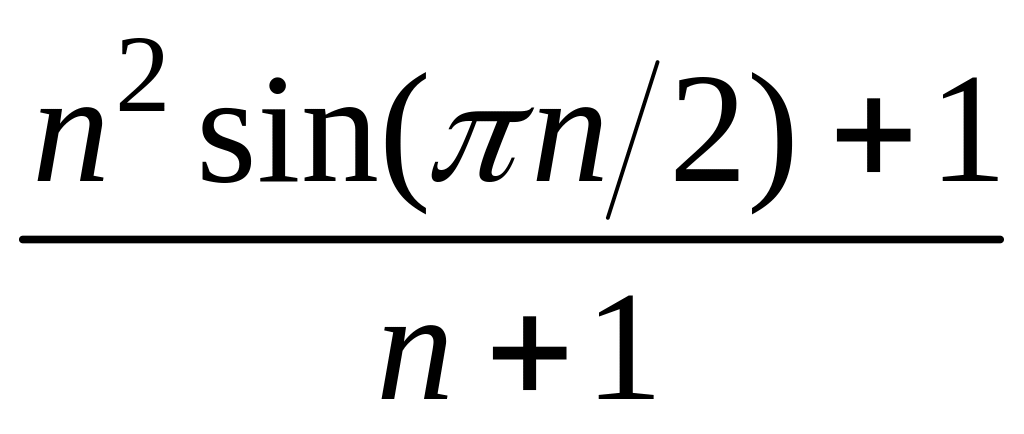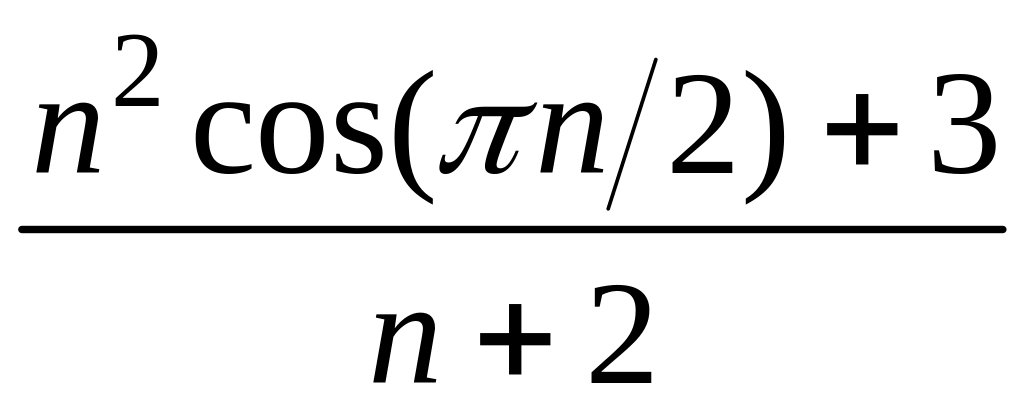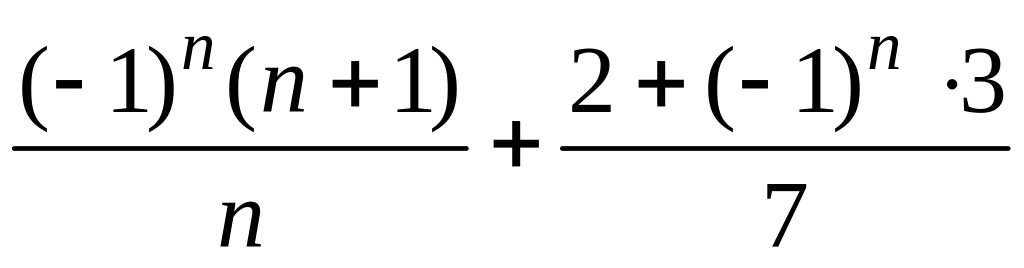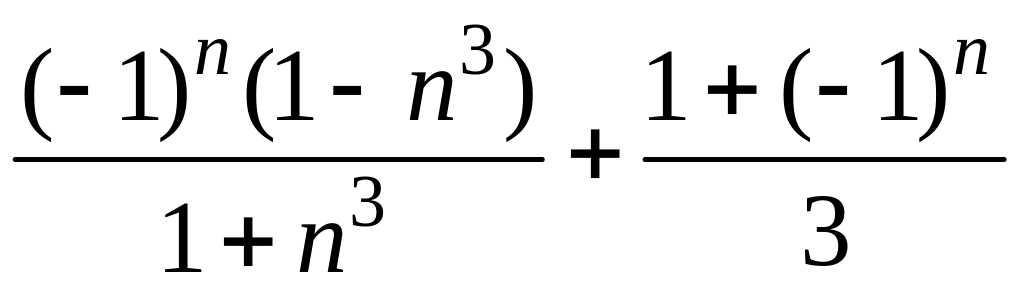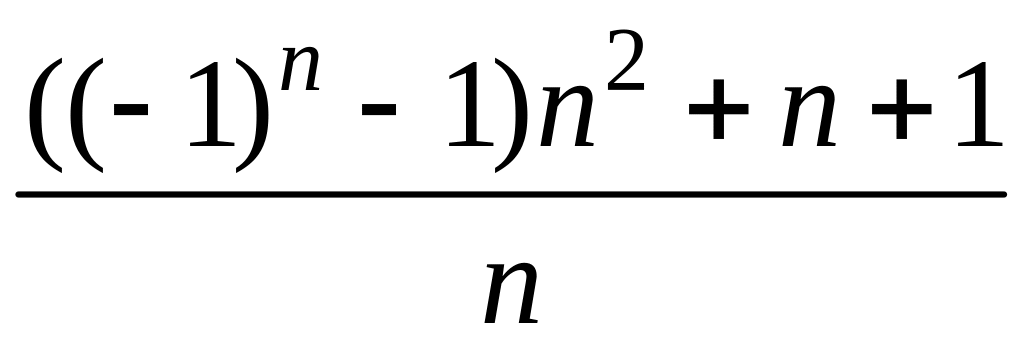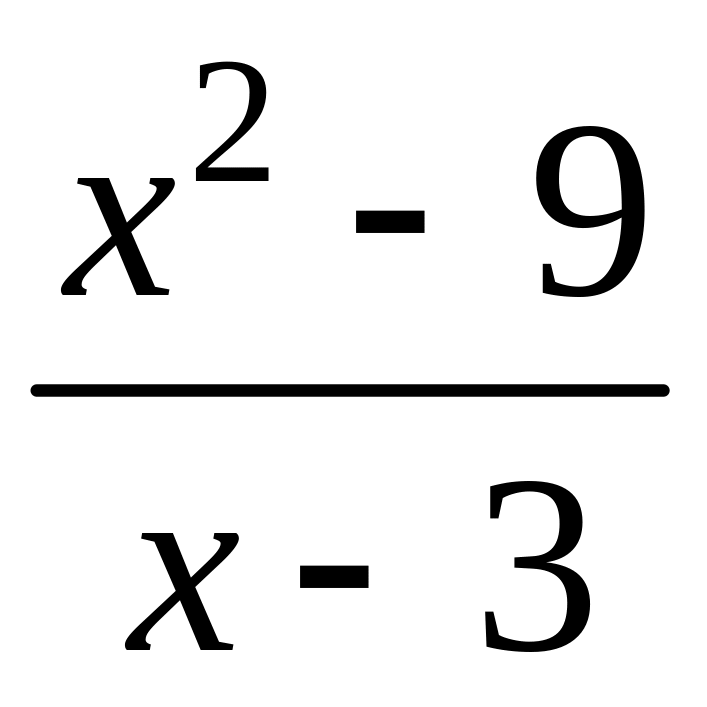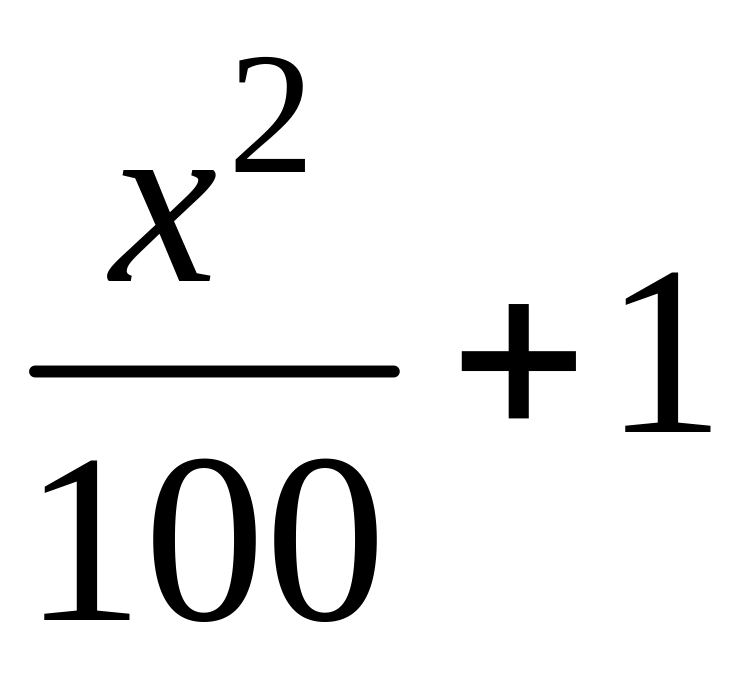- •1 Пользуясь критерием Коши, доказать сходимость или расходимость последовательности :
- •2 Пользуясь теоремой о существовании предела монотонной и ограниченной последовательности, доказать сходимость последовательности :
- •3 Вычислить :
- •4 Вычислить :
- •5 Для последовательности найти и :
- •Решение типовых примеров
- •2.20 Пользуясь теоремой о существовании предела монотонной и ограниченной последовательности, доказать сходимость последовательности
- •2 Пользуясь определением предела по Коши (на «языке »), доказать, что .
- •3 Используя определение предела функции по Гейне (на языке последовательностей), доказать, что не существует предела .
- •4 Используя логические символы (на языке « ») сформулировать утверждение и привести соответствующие примеры.
- •5 Найти односторонние пределы или показать, что эти пределы не существуют. Если существует , найти его.
- •6 Пользуясь определение предела по Коши, доказать, что число не является .
- •Решение типовых примеров
- •2 Используя свойства пределов и первый замечательный предел, вычислить :
- •3 Используя свойства пределов, второй замечательный предел и равенства , , вычислить :
- •4 Используя свойства пределов, известные пределы, предел , вычислить :
- •1 Определить порядок относительно бесконечно малой при (при ) функций :
- •2 Для бесконечно малых при (при ) функций и выяснить, какие из следующих соотношений верны: 1) , 2) , 3) , 4) , 5) , 6) :
- •3 Для бесконечно малой при (при ) функции найти бесконечно малую при функцию вида ( ) такую что: 1) , 2) при :
- •4 Вычислить , используя принцип эквивалентности бесконечно малых:
- •Решение типовых примеров
5 Для последовательности найти и :
№ |
|
№ |
|
1 |
2 |
3 |
4 |
5.1 |
|
5.11 |
|
5.2 |
|
5.12 |
|
5.3 |
|
5.13 |
|
1 |
2 |
3 |
4 |
5.4 |
|
5.14 |
|
5.5 |
|
5.15 |
|
5.6 |
|
5.16 |
|
5.7 |
|
5.17 |
|
5.8 |
|
5.18 |
|
5.9 |
|
5.19 |
|
5.10 |
|
5.20 |
|
Решение типовых примеров
1.19 Пользуясь критерием Коши, установить сходимость или расходимость последовательности
![]() ,
где
,
.
,
где
,
.
Решение. Согласно критерию Коши, последовательность сходится тогда и только тогда, когда она фундаментальна, то есть
![]()
![]()
![]() :
:
![]() .
.
Возьмем любое
![]() и рассмотрим разность
и рассмотрим разность
![]()
![]()
![]()
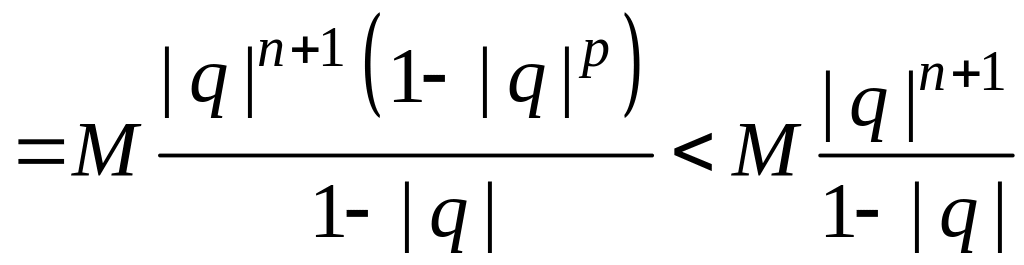 .
.
Найдем теперь
![]() из неравенства
из неравенства
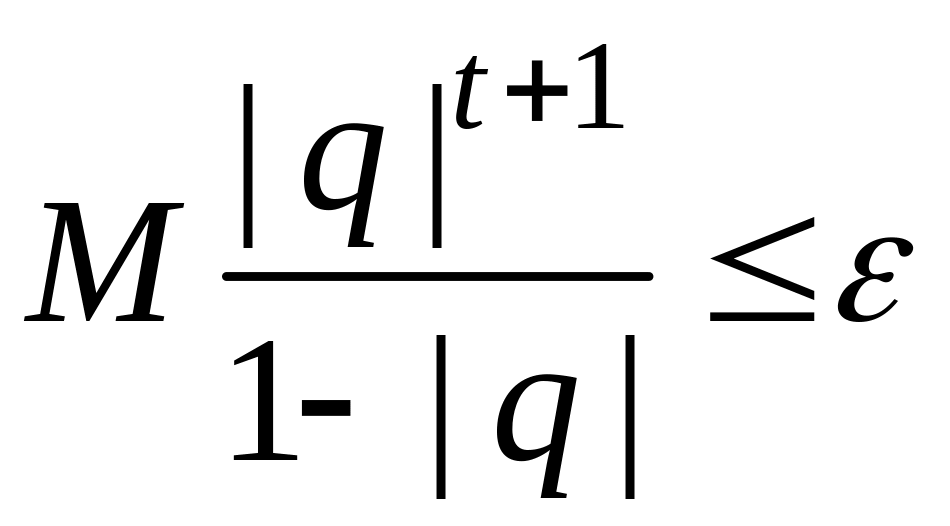 .
Имеем
.
Имеем
![]() .
Следовательно,
.
Следовательно,
![]() .
Полагая теперь
.
Полагая теперь
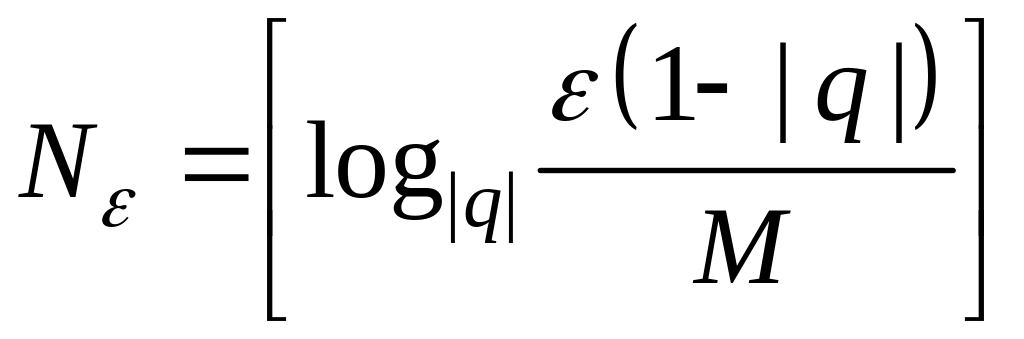 ,
получим, что при
,
получим, что при
![]()
![]() и
выполняется неравенство
и
выполняется неравенство
![]() .
.
Таким образом, последовательность является фундаментальной и, согласно критерию Коши, сходится.
1.20 Пользуясь
критерием Коши, установить сходимость
или расходимость последовательности
![]() .
.
Решение. Покажем, что данная последовательность не сходится. Для этого достаточно показать, что она не удовлетворяет критерию Коши, то есть
![]()
![]()
![]() :
:
![]() .
.
В нашем случае
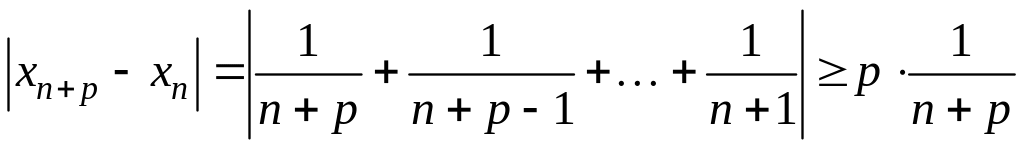 .
.
Пусть
![]() .
Тогда получим
.
Тогда получим
![]() .
Рассмотрим
.
Рассмотрим
![]() .
В этом случае
.
В этом случае
![]() ,
,
![]()
![]() ,
т.е. последовательность не является
фундаментальной, а значит, и не сходится.
,
т.е. последовательность не является
фундаментальной, а значит, и не сходится.
2.20 Пользуясь теоремой о существовании предела монотонной и ограниченной последовательности, доказать сходимость последовательности
Решение. Так как
 ,
,
то – возрастает.
Покажем, что
последовательность ограничена. Учитывая
неравенство
![]() ,
,
![]() ,
имеем:
,
имеем:

![]()
 ,
,
т.е.
![]() .
Откуда
.
Откуда
![]() .
Значит,
– монотонна и ограничена. Тогда по
теореме о сходимости монотонной и
ограниченной последовательности
сходится.
.
Значит,
– монотонна и ограничена. Тогда по
теореме о сходимости монотонной и
ограниченной последовательности
сходится.
3.20 Вычислить пределы:
А)
![]() ,
Б)
,
Б)
 ,
В).
,
В).
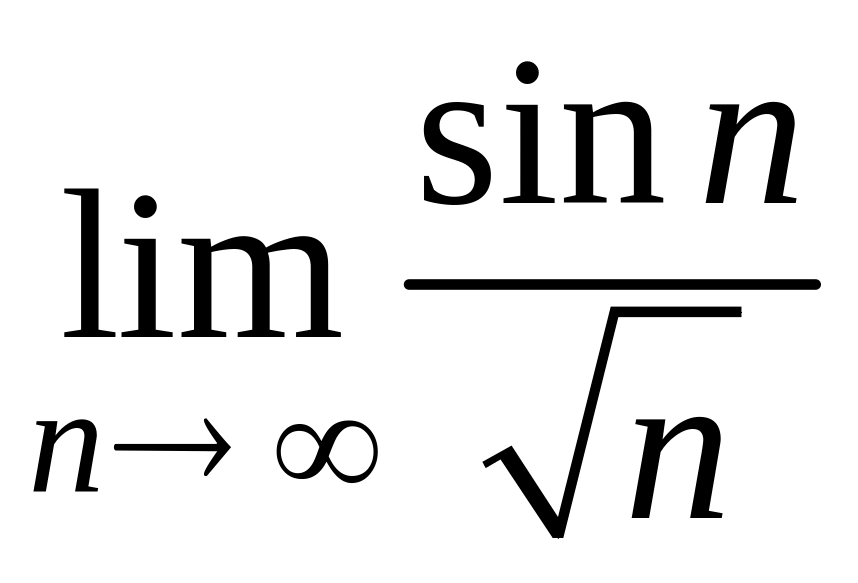 .
.
Решение.
А) Имеем:
![]()
=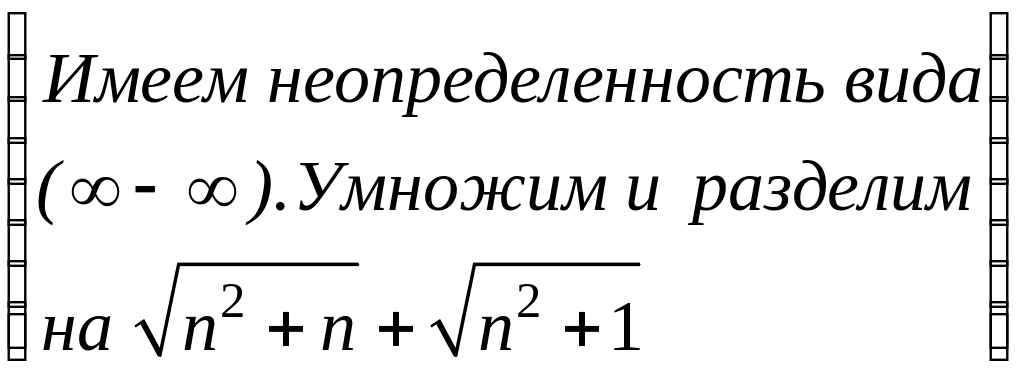 =
=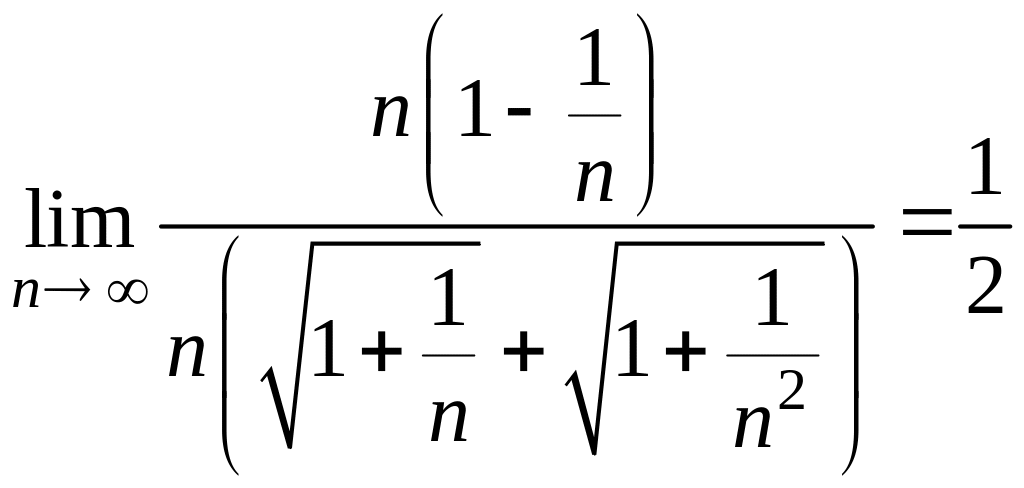 .
.
Б) Так как
 ,
то будем иметь
,
то будем иметь

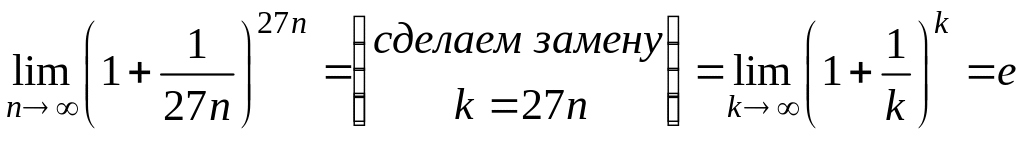 .
.
В) Поскольку
![]() а последовательность
а последовательность
![]() является бесконечно малой, то произведение
является бесконечно малой, то произведение
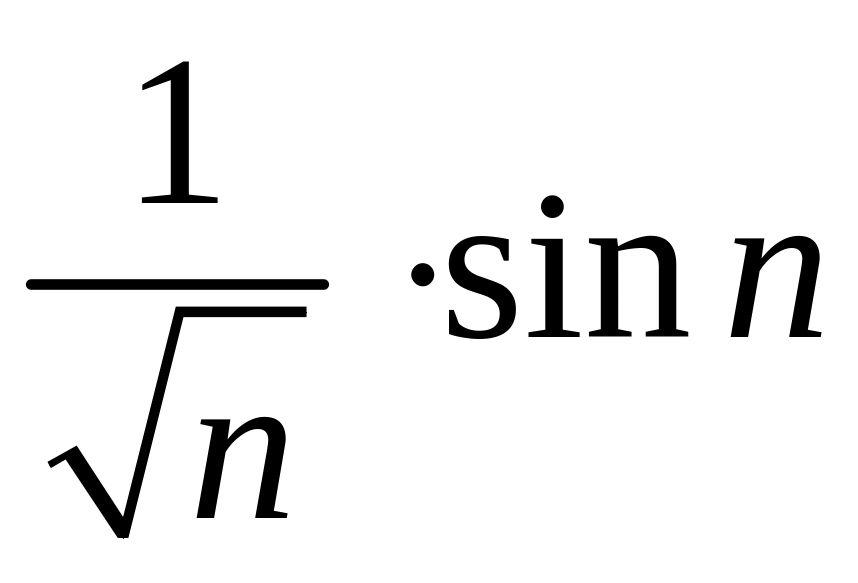 также будет бесконечно малой
последовательностью, т.е.
также будет бесконечно малой
последовательностью, т.е.
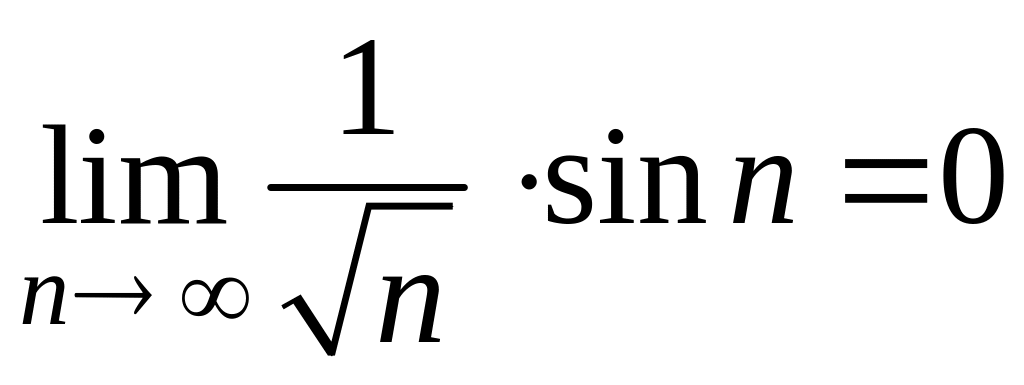 .
.
4.20 Вычислить пределы:
А)
![]() ,
Б)
,
Б)
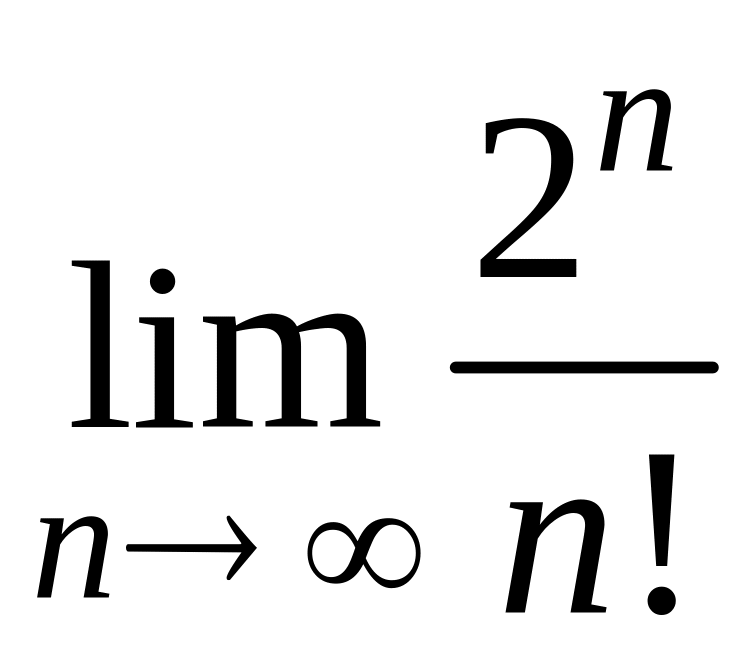 ,
В)
,
В)
![]() .
.
Решение.
А) Так как
![]() ,
то будем иметь
,
то будем иметь
![]() .
.
Б) Если
![]() то
то
![]() .
Поэтому при
.
Поэтому при
![]()
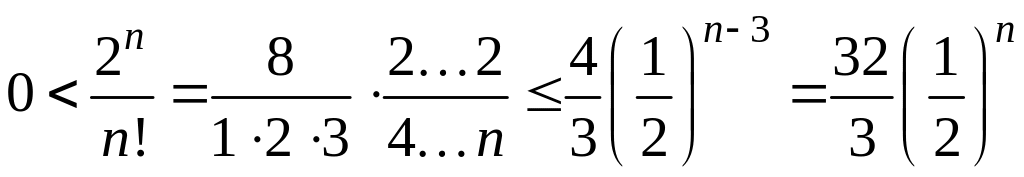 .
.
Так как
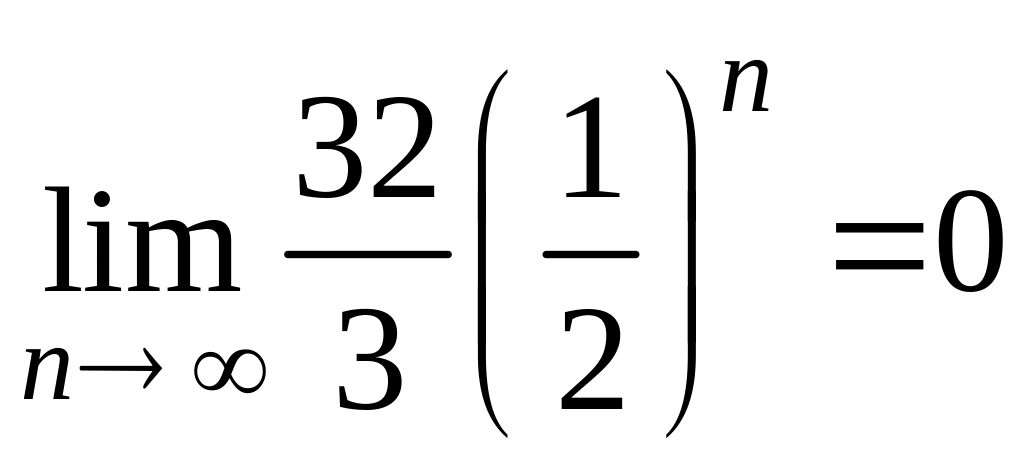 ,
то по теореме о предельном переходе в
неравенствах
,
то по теореме о предельном переходе в
неравенствах
 .
.
В) Так как
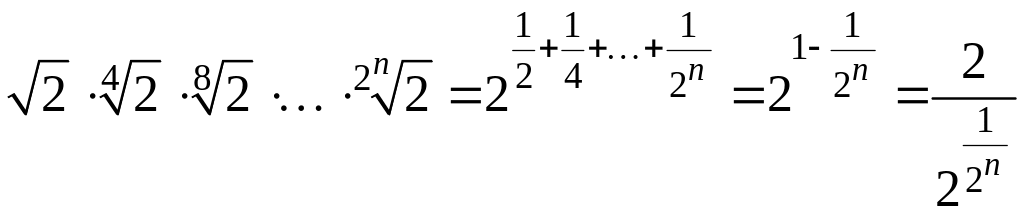 и при
и при
![]()
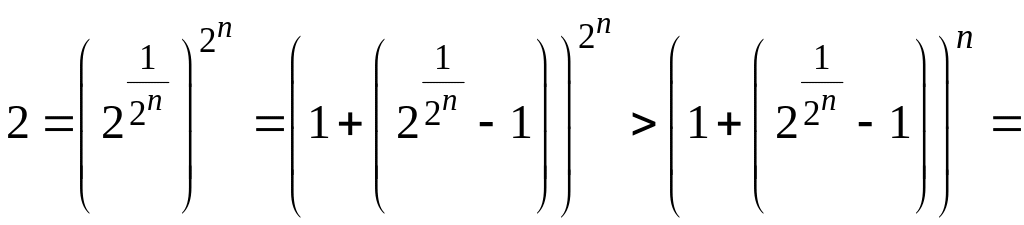

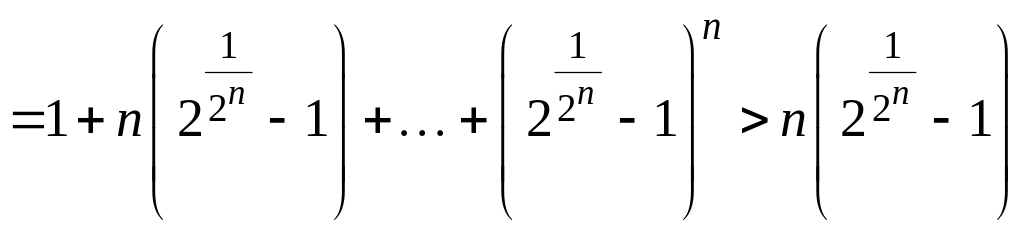 ,
,
т.е.
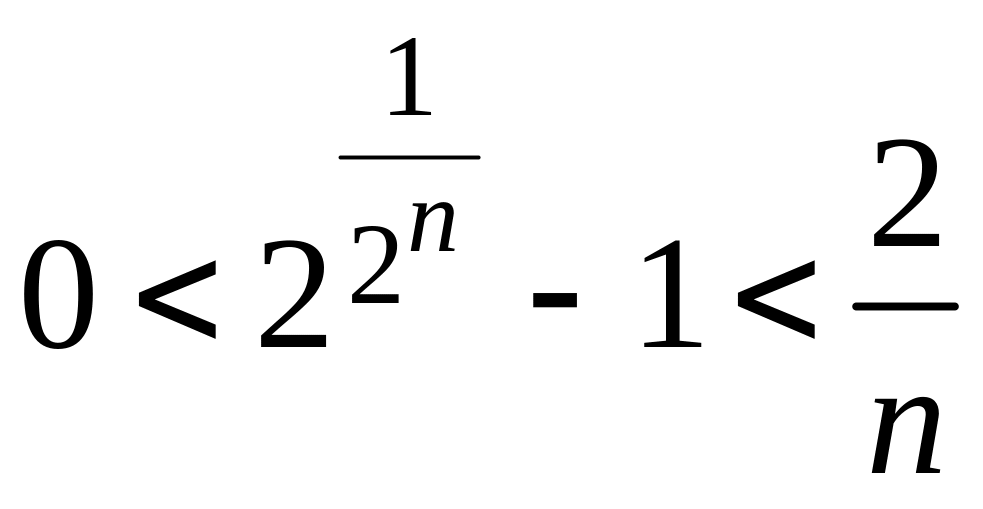 ,
то по теореме о предельном переходе в
неравенствах
,
то по теореме о предельном переходе в
неравенствах
![]() ,
то есть
,
то есть
![]() .
Следовательно,
.
Следовательно,
![]() .
.
5.20 Для последовательности = найти и .
Решение.
При
![]() имеем
имеем
![]() ,
и, значит,
,
и, значит,
![]() ,
,
![]() ,
причем
,
причем
![]() .
.
При
![]() или
или
![]() имеем
имеем
![]() ,
и, значит,
,
и, значит,
![]() ,
,
![]() .
.
При
![]() имеем
имеем
![]() ,
значит,
,
значит,
![]() ,
,
![]() .
.
Таким образом,
числа
![]() являются частичными пределами данной
последовательности. Рассмотренные
четыре подпоследовательности
являются частичными пределами данной
последовательности. Рассмотренные
четыре подпоследовательности
![]() ,
,
![]() ,
,
![]() ,
,
![]() составляют вместе всю данную
последовательность. Отсюда следует,
что других частичных пределов данная
последовательность не имеет.
составляют вместе всю данную
последовательность. Отсюда следует,
что других частичных пределов данная
последовательность не имеет.
Очевидно,
![]() ,
,
![]() .
.
Лабораторная работа № 7
Предел функции
Необходимые понятия и теоремы: различные определения предела функции, общие свойства предела функции, предел и неравенства, предел и арифметические операции, предел композиции, критерий Коши существования предела, односторонние пределы, бесконечные пределы, частичные пределы.
Литература: [1] с. 163 – 180, [5] с. 47 – 72.
1 Для
функции
![]() ,
,
![]() ,
заданных
,
заданных
![]() ,
,
![]() и
и
![]() найти такое
найти такое
![]() ,
чтобы для любых
,
удовлетворяющих условию 0<
,
чтобы для любых
,
удовлетворяющих условию 0<![]() <
,
выполнялось неравенство
<
,
выполнялось неравенство
![]() <
<
№ |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1.1 |
|
|
0 |
1 |
0,1 |
0,001 |
1.2 |
|
|
1 |
|
0,01 |
0,001 |
1.3 |
|
|
1 |
1 |
0,1 |
0,002 |
1.4 |
|
|
|
1 |
0,01 |
0,001 |
1.5 |
|
|
0 |
1 |
0,1 |
0,01 |
1.6 |
|
|
1 |
1 |
0,01 |
0,001 |
1.7 |
|
|
3 |
6 |
0,1 |
0,001 |
1.8 |
|
|
0 |
|
0,02 |
0,002 |
1.9 |
|
|
1 |
1 |
0,3 |
0,003 |
1.10 |
|
|
1 |
1 |
0,1 |
0,01 |
1.11 |
|
|
0 |
1 |
0,2 |
0,01 |
1.12 |
|
|
1 |
0 |
1 |
0,001 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1.13 |
|
|
|
1 |
0,01 |
0,001 |
1.14 |
|
|
|
-1 |
0,1 |
0,002 |
1.15 |
|
|
3 |
4 |
1 |
0,0001 |
1.16 |
|
|
0 |
1 |
0,1 |
0,001 |
1.17 |
|
|
0 |
1 |
0,1 |
0,01 |
1.18 |
|
|
0 |
0 |
0,1 |
0,001 |
1.19 |
|
|
1 |
2 |
0,2 |
0,01 |
1.20 |
|
|
1 |
3 |
0,1 |
0,001 |