4.4. Статистические оценки параметров линейной корреляционной зависимости (между двумя случайными величинами)

Если случайные величины X и Y связаны линейной корреляционной зависимостью, то уравнение регрессии Y на X - т.е. условное математическое ожидание случайной величины Y является функцией от х, и эта функция - линейная) имеет вид: .

Аналогично уравнение регрессии Х на Y или прямая регрессия Х на Y есть: .

Коэффициенты уравнений регрессии находят методом наименьших квадратов, то есть из условия, что сумма квадратов отклонений возможных значений случайной величины от теоретических значений (рассчитанных по уравнению регрессии) имеет минимум при данных значениях коэффициентов уравнения регрессии. Полученные этим методом коэффициенты имеют вид:

. ,

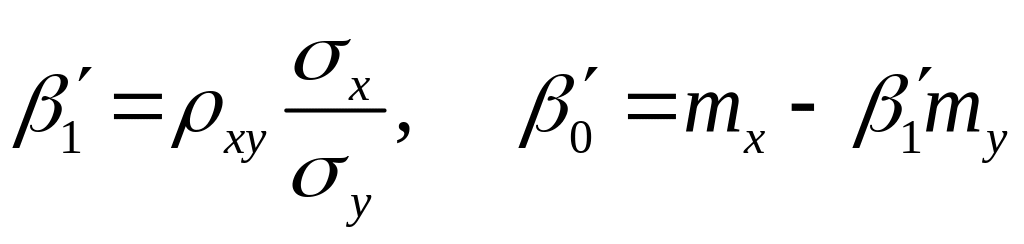здесь - математическое ожидание и дисперсия случайной величины ,

- коэффициент корреляции между случайными величинами и ( - корреляционный момент (ковариация)).

Пусть в результате эксперимента получена выборка . Предварительное представление о зависимости между Х и Y можно получить, отмечая элементы выборки в виде точек на плоскости с выбранной системой координат. Такое представление выборки системы двух случайных величин называется диаграммой рассеивания.

Если есть основания предполагать, что существует линейная корреляционная зависимость между Х и Y, то можно решить следующие задачи статистики.

Задача 1. Точечные оценки математических ожиданий, дисперсий, ковариации, коэффициента корреляции и коэффициентов уравнений регрессии: можно рассчитать по формулам:

,

, ,

, .

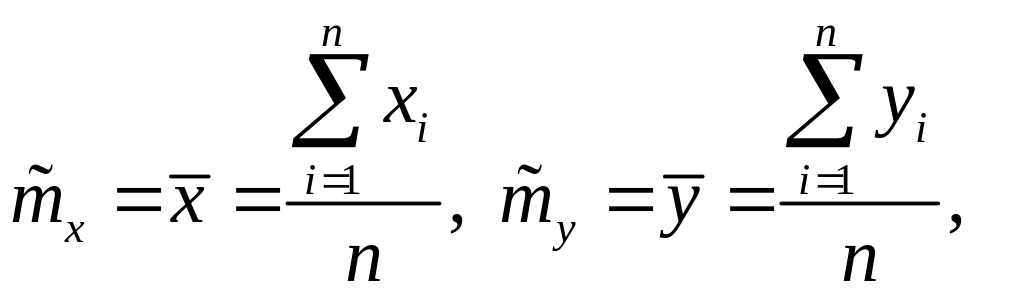
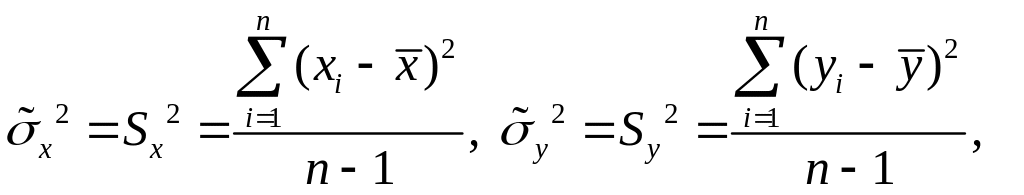
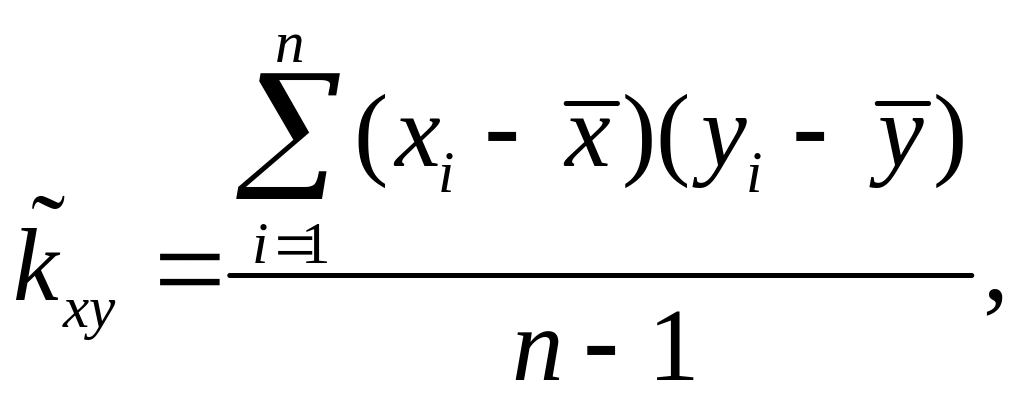
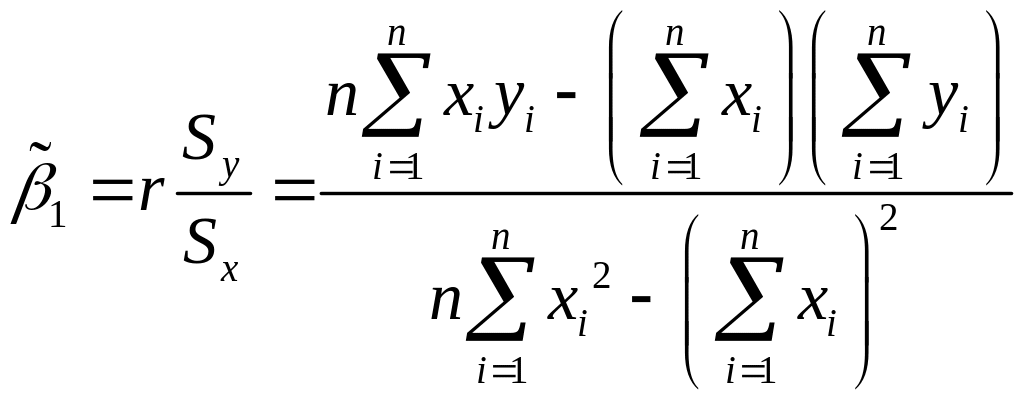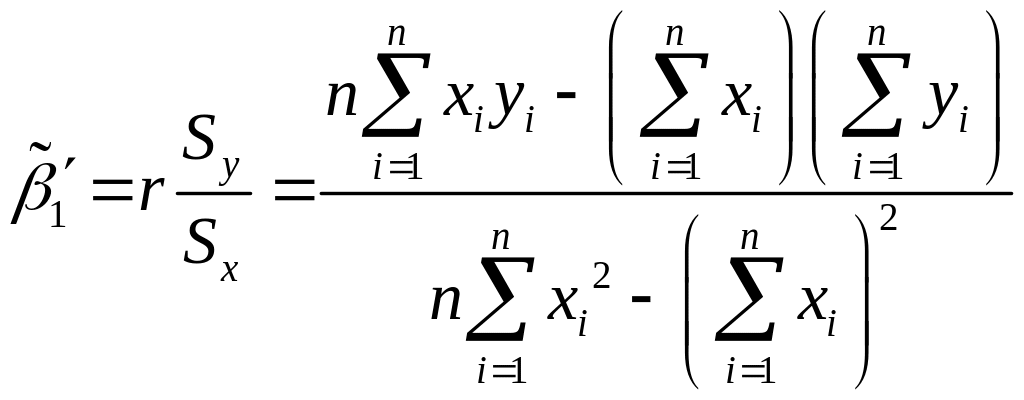Для контроля правильности вычислений используют соотношение

.

Задача 2. Для построения доверительного интервала для коэффициента корреляции можно воспользоваться тем обстоятельством, что статистика имеет приближенно нормальное распределение с математическим ожиданием и дисперсией при сравнительно небольших объемах выборки . Тогда доверительный интервал для при уровне значимости ( - доверительная вероятность) будет , здесь - квантиль порядка нормального распределения. Доверительный интервал для коэффициента корреляции вычисляют с помощью таблиц гиперболического тангенса , то есть .

Задача 3. При проверке статистической гипотезы , т.е. гипотезы о том, что нормально распределенные случайные величины Х и Y некоррелированы, используют статистику 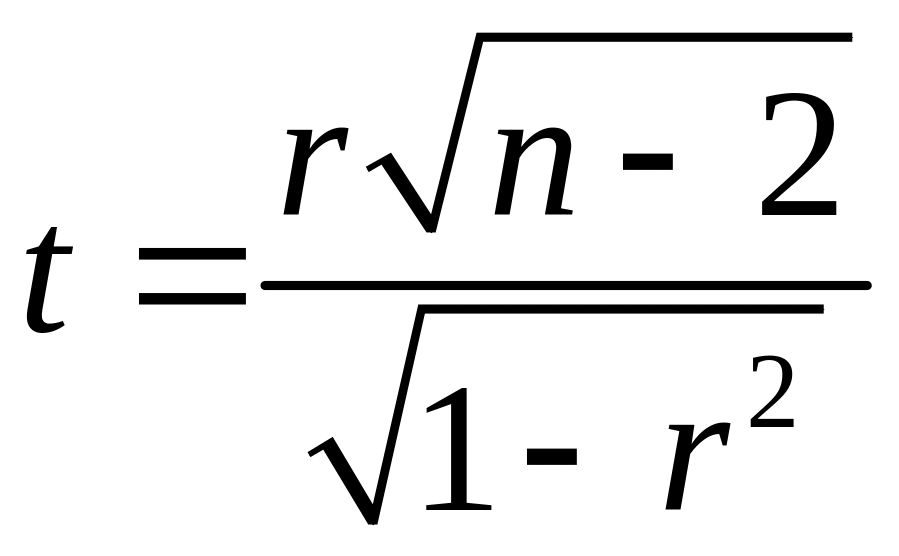, которая имеет распределение Стьюдента с степенями свободы. Если окажется, что 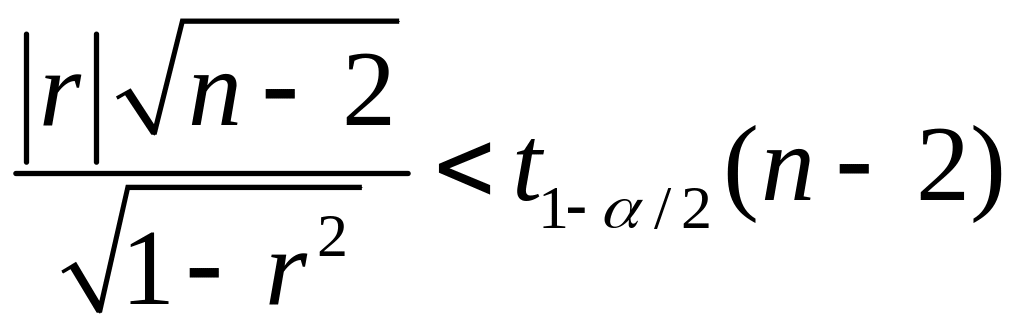, то гипотезу принимают при уровне значимости .

5. Контрольная работа № 7. Задания

1. Записать комплексное число в трех формах записи. Вычислить: . Найти все значения корня: (таблица 1).

2. Вычислить интегралы от функций комплексного переменного (таблица 2).

3. Исследовать сходимость положительных числовых рядов (таблица 3).

4. Разложить функцию в ряд по степеням . Найти радиус и область сходимости ряда (табдица 4).

5. Разложить функцию в ряд Фурье (таблица 5).

5.1. Пример выполнения контрольной работы № 1. Вариант 0.

1. Записать комплексное число в трех формах записи. Вычислить: . Найти все значения корня: : .

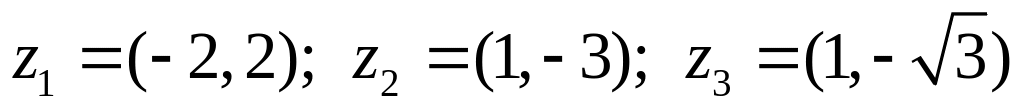Решение. Рассмотрим число - это общая форма комплексного числа. Тогда это число можно изобразить точкой на комплексной плоскости (или радиус-вектором). Запишем его в трех других формах. Для этого вычислим модуль и главное значение аргумента данного числа (модуль комплексного числа – есть расстояние от этой точки до начала координат (или длина радиус-вектора), а аргумент – есть угол между положительным направлением оси и радиус-вектором точки (отсчет против часой стрелки). Аргумент вычисляется с точностью до , поэтому выделяют главное значение аргумента):

,

(т.к. ).

Тогда: - алгебраическая форма записи числа;

- тригонометрическая форма записи числа;

- показательная форма записи числа.

Вычислим теперь значение выражения: .

Для этого воспользуемся алгебраической формой комплексных чисел:

. Имеем:

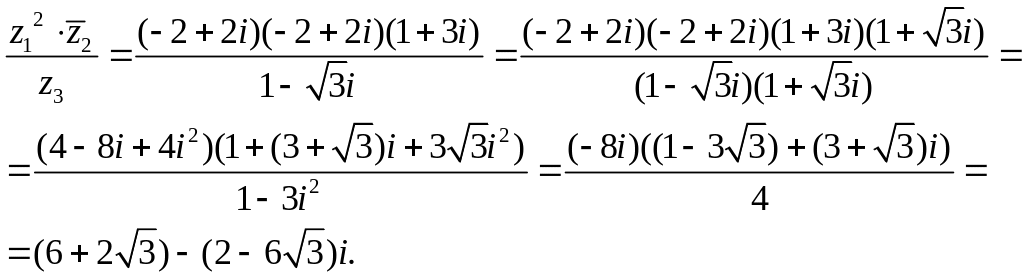
Для того, чтобы найти все значения корня из комплексного числа удобно записать его в тригонометрической форме. Сначала найдем модуль и аргумент числа . Получим: .

Используем формулу извлечения корня из комплексного числа:

Подставим найденные значения:

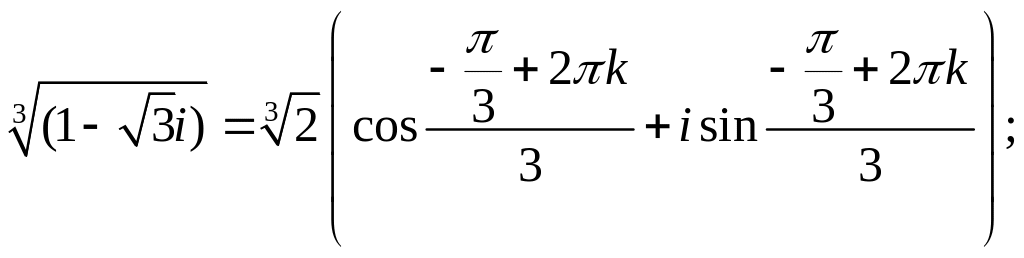
Подставляя 3 значения , окончательно получаем 3 значения корня:

Ответ. ; ;

2. Вычислить интегралы от функций комплексного переменного.

а) , где L – линия, соединяющая точки и .

Решение. Так как подынтегральная функция не является аналитической, то используем общую формулу сведения интеграла от комплексной функции к криволинейным интегралам от вещественных функций: .

Для комплексного числа сопряженным является число , тогда для функции имеем: . Кривая - есть отрезок, соединяющий точки и , уравнение этой кривой: . Тогда вдоль этой кривой: и:

= .

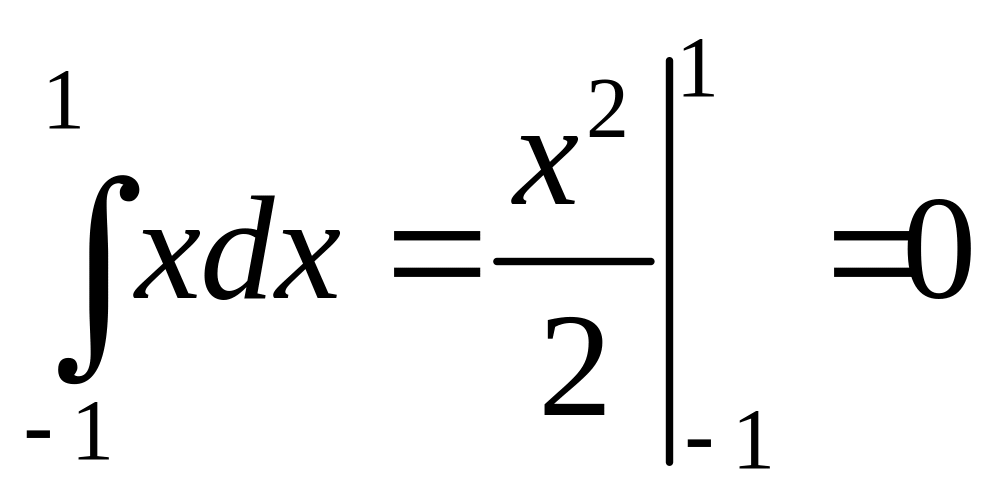б) Использовать интегральную формулу Коши: ,

L – окружность: .

Решение. Рассмотрим подынтегральную функцию . Ее особые точки (в которых знаменатель обращается в 0) . Одна из них не принадлежат области, охватываемой кривой L, а вторая принадлежит этой области (см. Рис.10), поэтому в этой области функция не является аналитической.

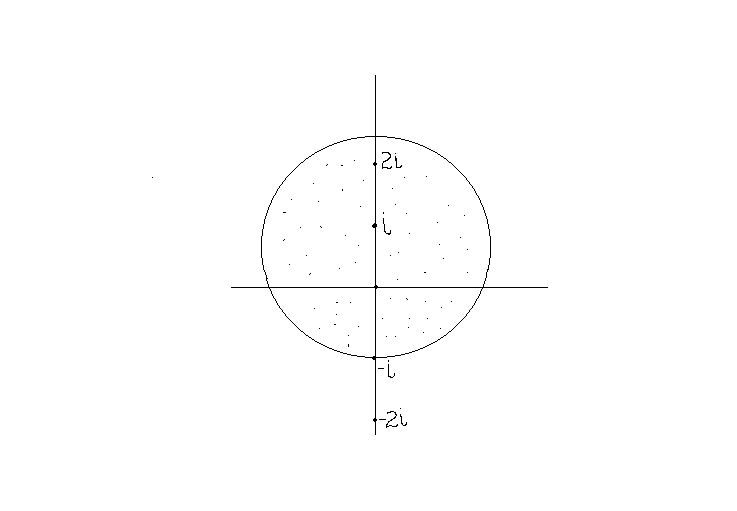
Рис. 10

Интеграл можно переписать в виде: 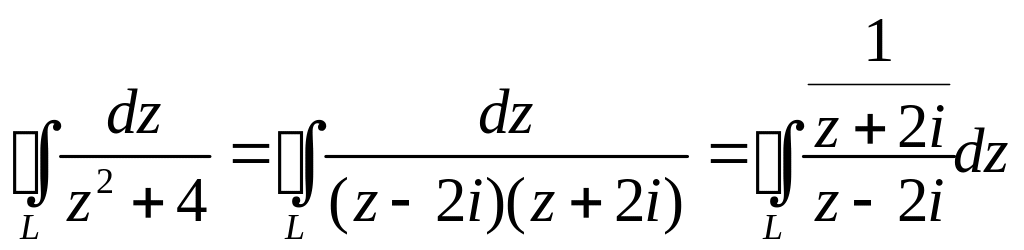, при этом функция, стоящая в числителе: , аналитическая в области, ограниченной контуром L, и точка охватывается контуром L. Применяя интегральную формулу Коши: , получаем:

.

Ответ. а) =0; б) .

3. Исследовать сходимость положительных числовых рядов.

Решение. а) .Общий член данного ряда: . Для исследования сходимости, сначала проверяем выполнение необходимого признака сходимости. 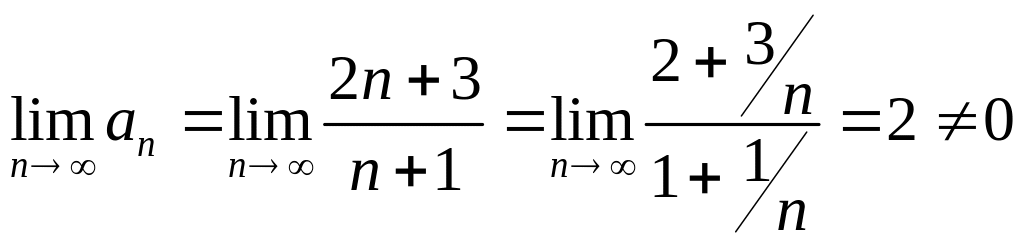; необходимый признак не выполняется, значит, ряд расходится.

б) . Общий член данного ряда . Проверим выполнение необходимого признака сходимости: , значит, данный ряд может сходиться и расходиться. Применим достаточный признак сходимости, воспользуемся признаком Даламбера: , , тогда 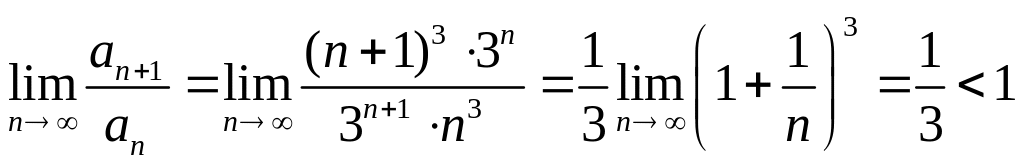. Следовательно, данный ряд сходится.

Ответ. Ряд расходится; ряд сходится.

4. Разложить функцию в ряд по степеням . Найти радиус и область сходимости ряда.

Решение.

Если функция f(x) – бесконечное число раз непрерывно дифференцируемая, то она может быть разложена в степенной ряд по формуле:

.

Этот ряд называется рядом Тейлора для функции f(x) (если разложение в точке , то ряд называется рядом Маклорена). В области сходимости сумма этого ряда совпадает с функцией f(x).

При разложении функции в степенной ряд можно использовать общую формулу или известные разложения основных элементарных функций в ряд Маклорена ( п.2.2.2.).

Преобразуем рассматриваемую функцию и воспользуемся разложением: . Имеем:

.

Разложим сначала в ряд функцию

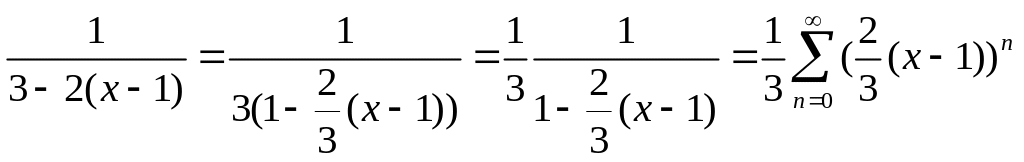. Область сходимости этого ряда . Степенной ряд в области сходимости можно дифференцировать почленно, поэтому

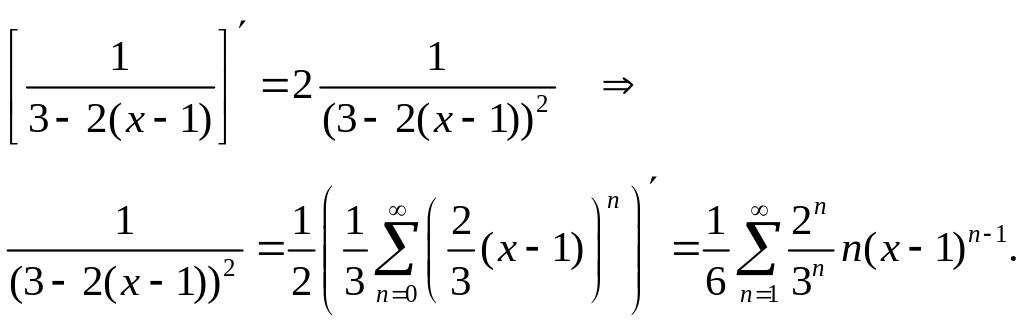
Таким образом, мы получили разложение в ряд для второго слагаемого. Аналогично, для первого слагаемого имеем:

.

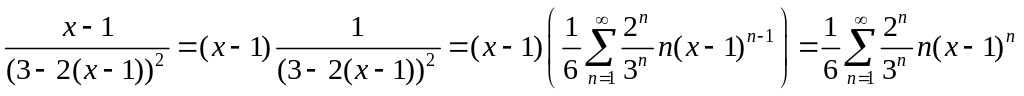Складывая эти два ряда, получаем

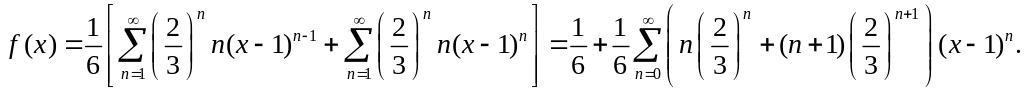
Область сходимости этого ряда - это круг с центром 1 и радиусом 3/2. Таким образом, радиус сходимости – 3/2.

Ответ: Степенной ряд имеет вид -

Радиус сходимости - 3/2, область сходимости .

5. Разложить в ряд Фурье функцию периода , заданную на отрезке формулой: .

Решение. Функция является кусочно-непрерывной, поэтому удовлетворяет условиям Дирихле, значит, эту функцию можно разложить в ряд Фурье, сходящийся к ней в точках непрерывности. Данная функция не является ни четной, ни нечетной, поэтому требуется найти все коэффициенты ряда. Имеем: ,

= + .

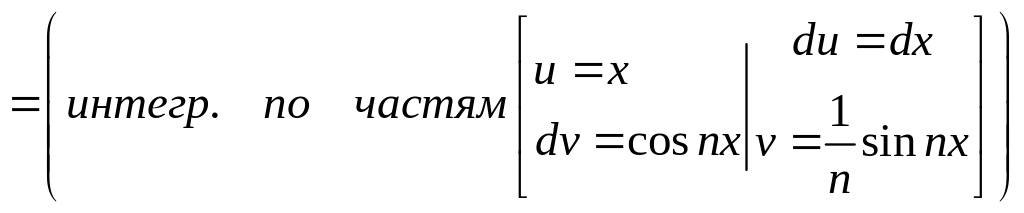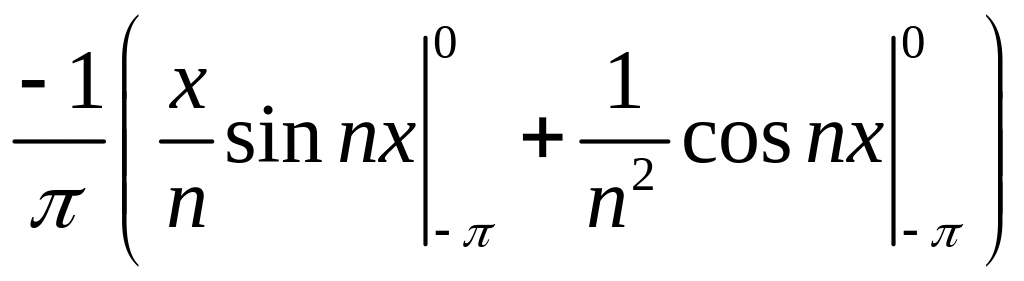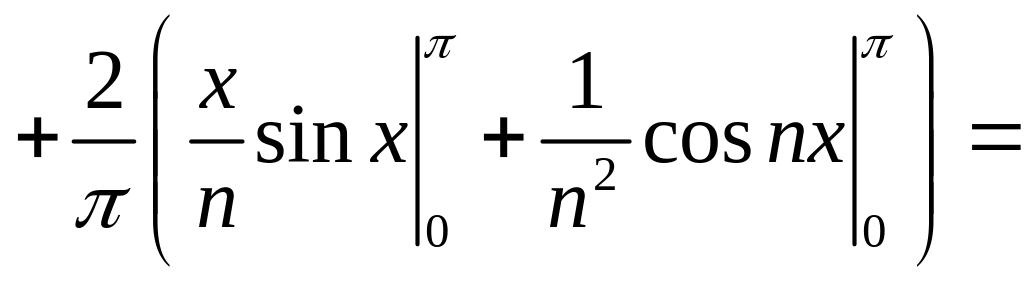
Аналогично находим .

Исходной функции соответствует ряд Фурье . Функция непрерывна во всех внутренних точках отрезка , поэтому, для всех этих точек имеем равенство: , т.е. .

В точках сумма ряда равна .

Графики функций и показаны на Рис. 11.

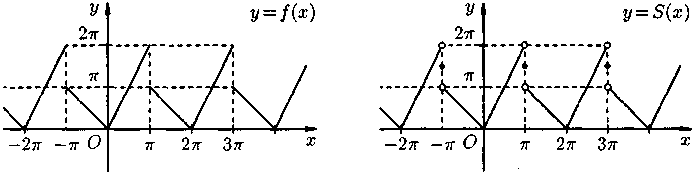
Рис. 11

Ответ. Разложение в ряд Фурье имеет вид: .