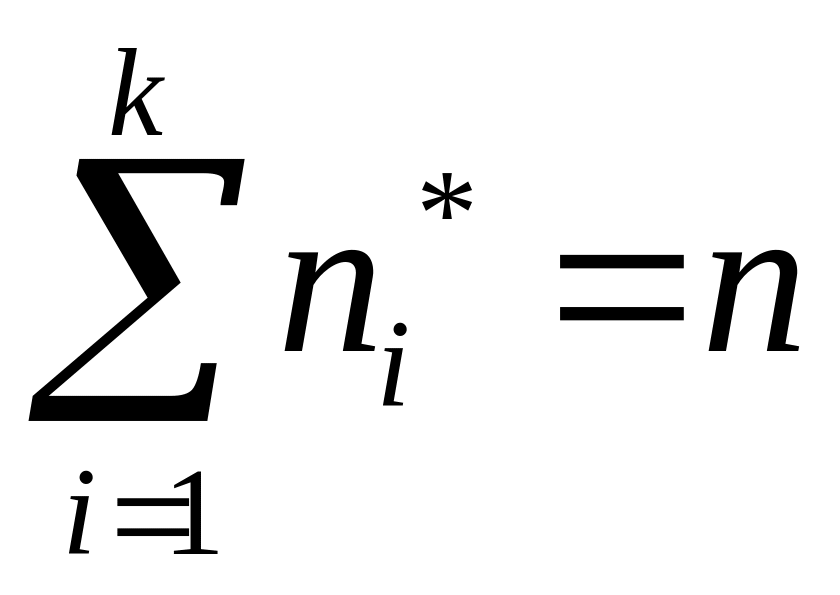- •Оглавление
- •Введение
- •1. Теория функций комплексного переменного
- •Комплексные числа и операции над ними
- •1.1.1. Определение комплексного числа
- •1.1.2. Формы записи комплексных чисел
- •1.1.3. Формула Муавра и извлечение корня n-ой степени из комплексного числа
- •1.2. Функции комплексного переменного
- •1.3. Дифференцирование функций комплексного переменного
- •1.3.1. Определение производной
- •1.3.2. Необходимые и достаточные условия дифференцируемости функции комплексного переменного
- •1.3.3. Производные основных элементарных функций
- •1.3.4. Восстановление аналитической функции по известной действительной или мнимой части
- •Интегрирование функций комплексного переменного
- •1.4.1. Определение интеграла от функции комплексного переменного
- •1.4.2. Теорема Коши. Вычисление интегралов от аналитических функций
- •2. Теория рядов
- •2.1. Числовые ряды
- •2.1.1.Основные понятия Пусть дана последовательность чисел (вещественных или комплексных)
- •Свойства сходящихся рядов
- •Замечание. Условие является необходимым, но не достаточным для сходимости, т.Е. Если , то ряд может сходиться, а может и расходиться.
- •Т. Е. Сходимость ряда равносильна тому, что сумма любого числа членов ряда, следующих за достаточно большим номером, должна быть произвольно мала.
- •2.1.2. Достаточные признаки сходимости положительных рядов
- •Пусть даны два положительных ряда и .
- •2.1.3. Сходимость рядов с произвольными членами
- •2.2. Функциональные ряды
- •2.2.1. Сходимость функционального ряда
- •Функциональные свойства суммы сходящегося ряда
- •2.2.2. Степенные ряды
- •Область сходимости степенных рядов
- •Ряды Тейлора и Маклорена
- •2.3. Ряды Фурье
- •2.3.1. Тригонометрический ряд Фурье. Периодические функции.
- •2.3.2. Сходимость ряда Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода 2l
- •2.3.3. Интеграл Фурье
- •3. Теория вероятностей
- •Случайные события и их вероятности
- •Классификация событий
- •3.1.2. Операции над событиями
- •3.1.3. Аксиоматическое определение вероятности
- •Примеры вероятностных пространств
- •Конечное вероятностное пространство
- •2. Непрерывное вероятностное пространство
- •3.1.4. Условная вероятность. Теорема умножения вероятностей.
- •3.1.5. Формула полной вероятности. Формула Байеса
- •3.1.6. Последовательность независимых испытаний. Формула Бернулли
- •3.1.7. Статистическое определение вероятности
- •3.2. Случайные величины, их распределения и числовые
- •3.2.1.Дискретные случайные величины
- •3.2.2. Функция распределения. Плотность распределения
- •3.2.3. Математическое ожидание случайной величины
- •3.2.4. Дисперсия случайной величины
- •3.2.5. Примеры законов распределения случайных величин Дискретные случайные величины
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределение
- •Непрерывные случайные величины
- •5. Равномерное распределение
- •6. Показательное распределение
- •7. Нормальное распределение
- •3.3. Системы случайных величин
- •3.3.1. Закон распределения системы случайных величин
- •Условный закон распределения
- •3.3.2. Числовые характеристики случайного вектора
- •3.3.3. Предельные теоремы теории вероятностей
- •4. Математическая статистика
- •4.1. Методы статистического описания результатов наблюдений
- •4.1.1. Статистическое распределение выборки
- •4.1.2. Эмпирическая функция распределения
- •4.2. Оценки параметров распределения
- •4.2.1.Точечные оценки параметров распределения
- •4.2.2. Интервальные оценки параметров распределения
- •4.3. Проверка статистических гипотез
- •4.4. Статистические оценки параметров линейной корреляционной зависимости (между двумя случайными величинами)
- •5. Контрольная работа № 7. Задания
- •5.1. Пример выполнения контрольной работы № 1. Вариант 0.
- •5.2. Варианты заданий контрольной работы № 7
- •6. Контрольная работа № 8. Задания
- •6.1. Пример выполнения контрольной работы № 2. Вариант № 0.
- •6.2. Варианты заданий контрольной работы № 8
4.1.2. Эмпирическая функция распределения
Пусть проведен эксперимент, связанный со случайной величиной Х и получена группированная выборка объема n из генеральной совокупности с функцией распределения ( группированный статистический ряд):
|
|
|
. . . |
|
|
|
|
|
. . . |
|
Определение.
Эмпирической
функцией распределения
(функцией распределения выборки)
называется числовая функция
![]() ,
определяемая соотношением:
,
определяемая соотношением:
![]() ,
где
,
где
![]() -
число опытов, в которых наблюдали
значения случайной величины Х
меньшие х,
т.е.
-
число опытов, в которых наблюдали
значения случайной величины Х
меньшие х,
т.е.
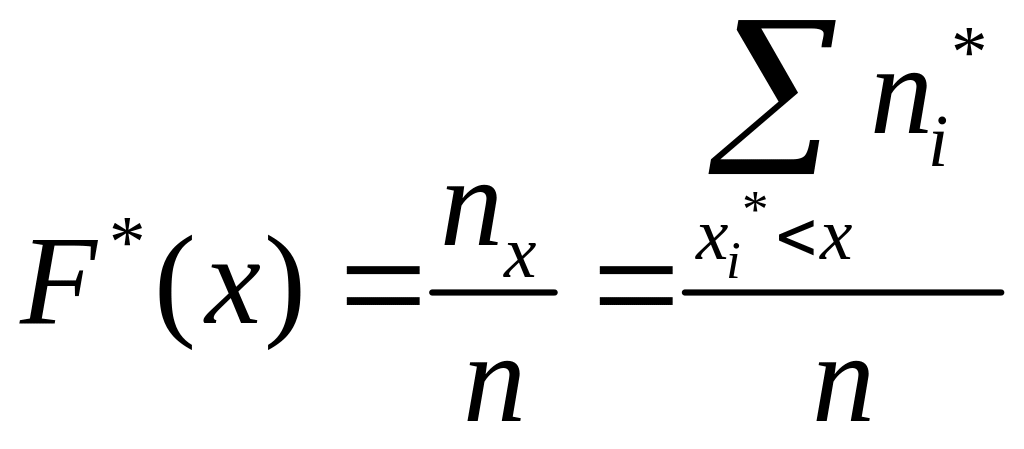 .
.
Замечание.
В отличие
от эмпирической функции распределения
,
функцию распределения генеральной
совокупности
называют теоретической
функцией распределения.
Отметим, что если значение теоретической
функции
![]() для каждого значения аргумента х
равно
вероятности осуществления события,
состоящего в том, что случайная величина
Х
приняла значение меньшее х,
то значение эмпирической функции
распределения
равно частоте осуществления того же
события.
для каждого значения аргумента х
равно
вероятности осуществления события,
состоящего в том, что случайная величина
Х
приняла значение меньшее х,
то значение эмпирической функции
распределения
равно частоте осуществления того же
события.
Свойства эмпирической функции распределения вытекают из ее определения:
Значения принадлежат интервалу
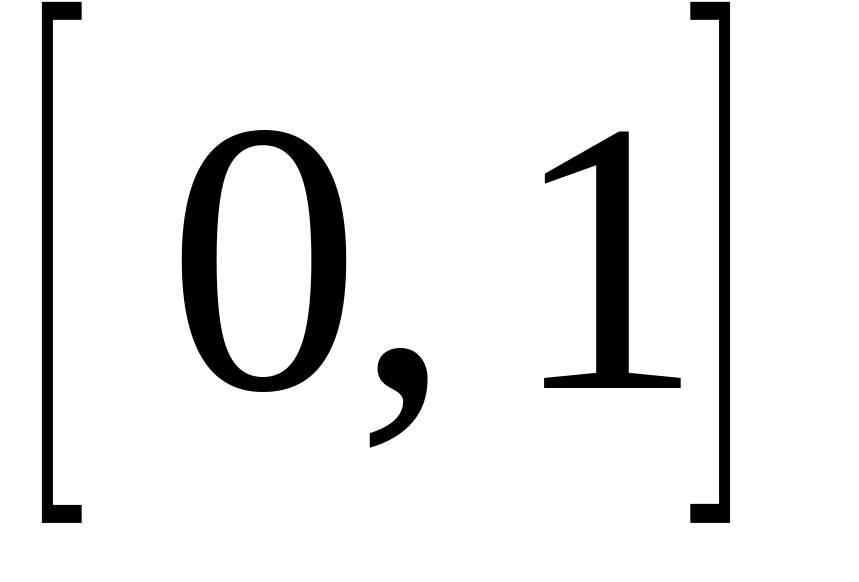 ,
,
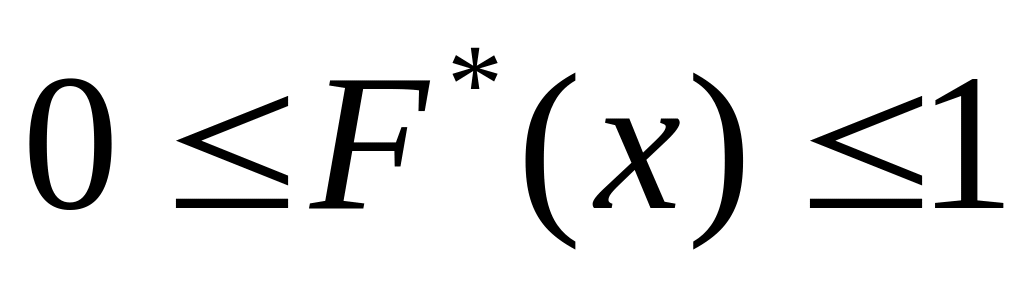 .
.Функция - неубывающая функция, то есть если
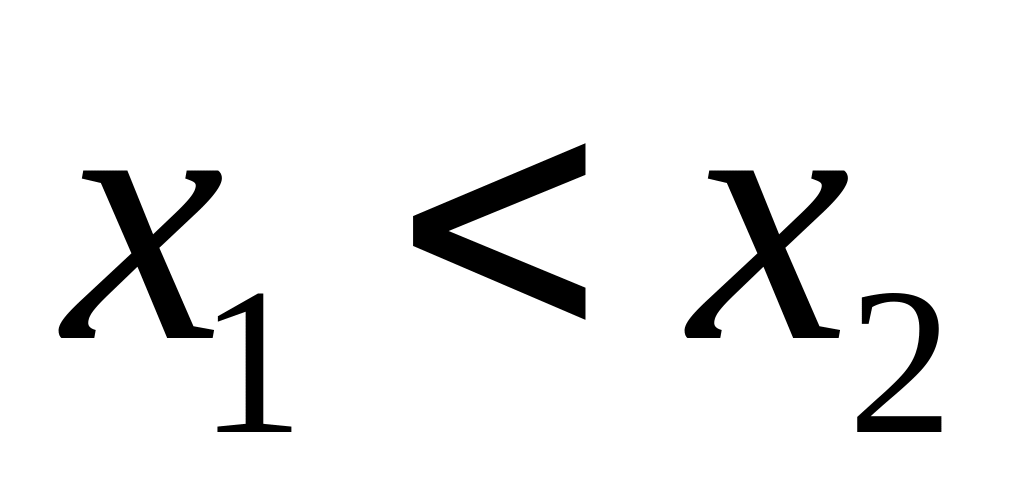 ,
то
,
то
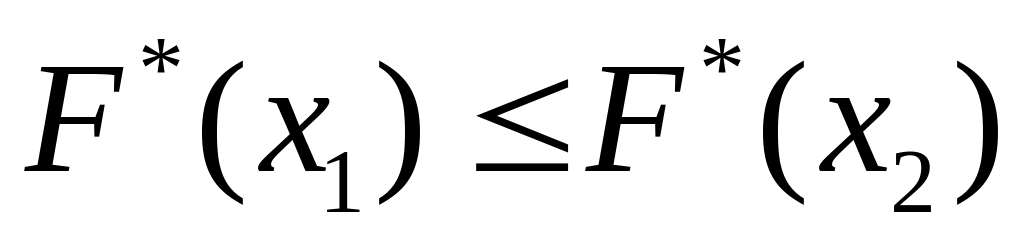 .
.Если
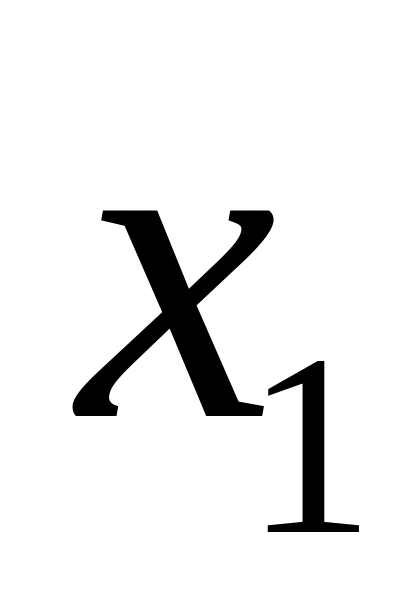 - наименьшая варианта, то при
- наименьшая варианта, то при

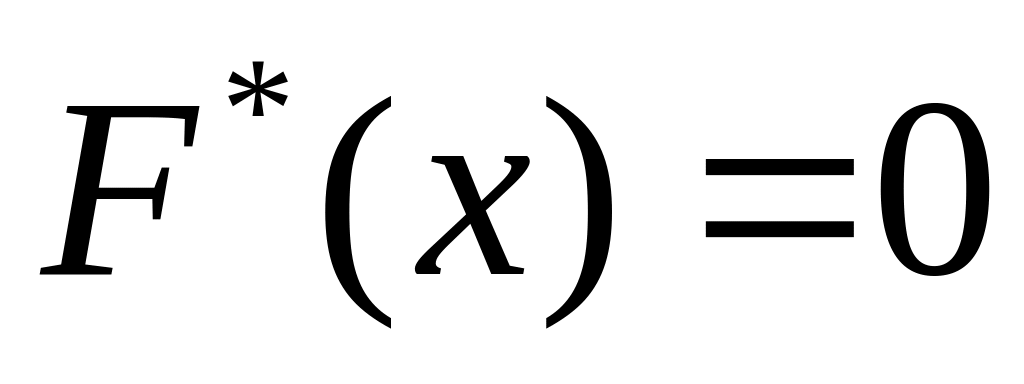 .
Если
.
Если
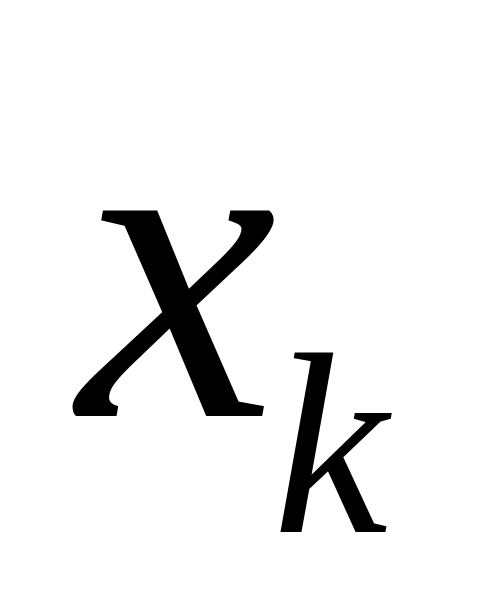 - наибольшая варианта, то при
- наибольшая варианта, то при
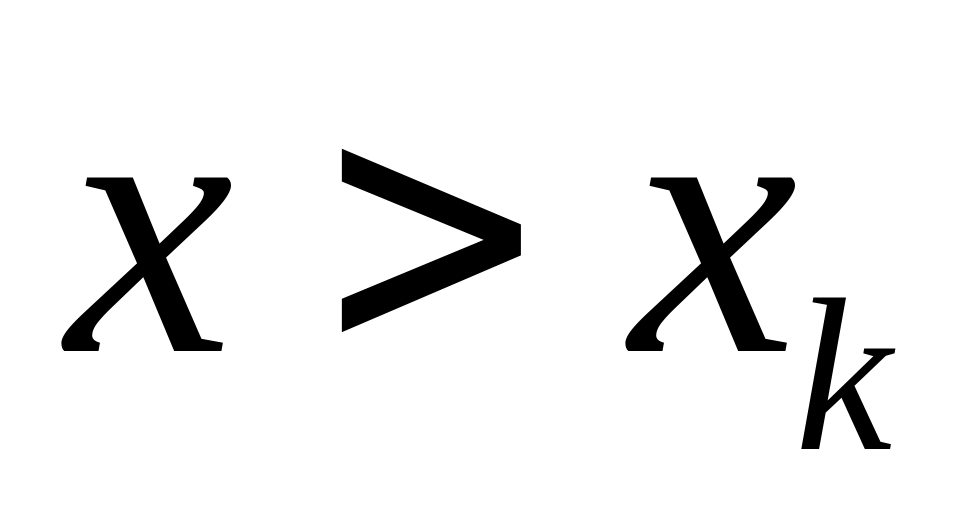
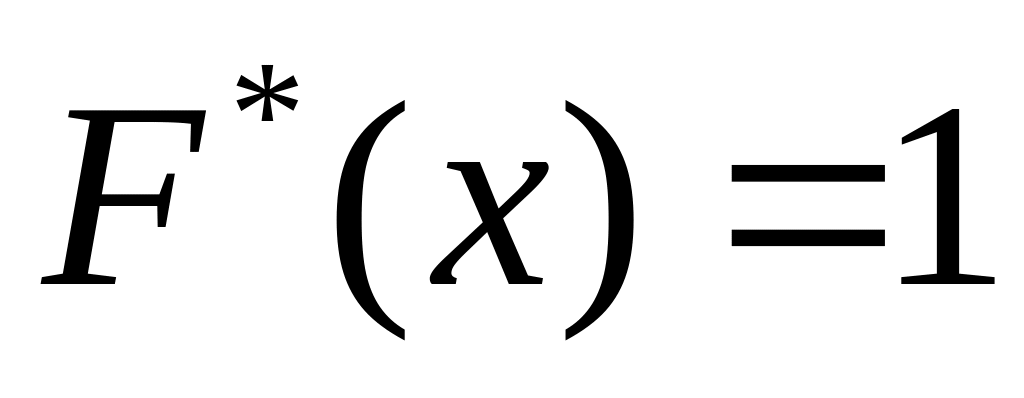 .
.
Пример. По данным примера из пункта 4.1.1. построить эмпирическую функцию распределения.
Решение.
Рассмотрим группированное статистическое распределение выборки:
|
11 |
13 |
15 |
17 |
19 |
21 |
23 |
|
0,0364 |
0,0727 |
0,1455 |
0,2182 |
0,2909 |
0,1818 |
0,0545 |
Вычислим значения , если попадает в каждый из интервалов группировки (для этого складываем относительные частоты всех предыдущих интервалов):
|
|
|
|
|
|
|
|
0 |
0,0364 |
0,1091 |
0,2546 |
0,4728 |
0,7637 |
|
|
|
|
0,9455 |
1,0000 |
Построим график этой таблично заданной функции, Рис. 9 (стрелками показано, какому из отрезков принадлежит концевая точка):
-

1-
 -
--
-
-
0,5-
-
-
-
-
 х
х10 12 14 16 18 20 22 24
Рис. 9