4.7. The exponential probability distribution
The exponential probability distribution is another important probability density function. This probability distribution is closely related to the Poisson probability distribution.
The
exponential probability distribution has only one parameter
,
which denotes the average number of occurrences per unit of time.
Remark:
The exponential distribution differs from the normal distribution in two important way
1. it is restricted to random variables with positive values;
2. its distribution is not symmetric.
Definition:
The exponential random variable X (x>0) has a probability density function
for
where
is the mean number of occurrences per unit time, x
is the number of
time units until the next occurrence, and
,
then X
is said to follow an exponential
probability distribution.
It can be shown
that
is
the same parameter used for the Poisson distribution and that the
mean time between occurrences is
.
The cumulative distribution function is
for
The
distribution has mean
and
variance
.
The
probability
for
the exponential probability distribution is given
by the area
in the tail of the exponential probability distribution curve
beyond
,
as it shown in Figure 4.22.
As we know
from earlier discussion, for a continuous random variable x,
is equal to
.
Hence for an exponential probability distribution,
=
=
By using the complementary probability rule, we obtain:
The probability that the x is between two successive occurrences is in the interval “a” to “b” is
.
Probabilities for the exponential probability distribution.
For the exponential probability distribution with the mean number of occurrences per unit of time equal to ,
=
.
Example:
A processing machine breaks down an average of once in four weeks. What is the probability that the next breakdown will not occur for at least six weeks after the previous breakdown? Assume that the time between breakdowns has an exponential distribution.
Solution:
Let x denote the lapse time between any two successive breakdowns of this machine. We are to find the probability
Because the unit of time for x is in the weeks, we must define the mean number of breakdowns per week. Since there is one breakdown in four weeks,
.
The required probability is calculated using the formula = .
In our
example,
and
.
The required probability is
=
.
The value
of
can
be found from the Table 1 of the Appendix.
Example:
A teller at the bank serves, on average, 30 customers per hour. Assume that the service time for a customer has an exponential distribution.
a) What is the probability that the next customer will take five minutes or more to be served?
b) Find the probability that the next customer will take two minutes or less to be served.
c) What is the probability the next customer will take two to four minutes to be served?
Solution:
Let x be the time taken by this teller to serve a customer. We must find the mean number of customers served per minute by this teller to define per unit of time (minute). The teller serves on average 30 customers per 60 minutes. Hence
=30/60=0.5 customers served per minute.
a) We need
to find the probability
.
(Fig. 4.23.)
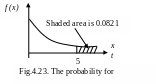In
this case a
=5.
=
=
The probability is 0.0821 that a customer will take more than five minutes
to be served.
b) We are
to find
.
This probability will be calculated using the formula
=
.
In this case a
= 2 minutes.
So
=
.
Thus, the probability is 0.6321 that a customer will be served in two minutes or less.
c)
Thus, the probability that the teller will take two to four minutes to serve a customer is 0.2325.
Exercises
1.
Let x
be a continuous random variable that possesses an exponential
probability distribution with
.
Find the following probabilities
a)
; b)
; c)
2. The life of a pie is exponentially distributed with a mean of three days. What is the probability that a pie that is baked just now will still be good after four days?
3. At the supermarket, a customer has to wait an average of four minutes in line before being served. The time a customer has to wait is exponentially distributed.
a) What is the probability that a customer will have to wait for more than eight minutes in line?
b) What is the probability that a customer will have to wait for three to seven minutes in line?
4. On average, 20 telephone calls are received per hour at an office. The time between calls received at this office is exponentially distributed.
a) What is the probability that no calls will come in during the next 10 minutes?
b) What is the probability that the next call will come in within 4 minutes?
5. Aysel works for a toy company and assembles five toys per hour on average. The assembly time for this toy follows an exponential distribution.
a) Find the probability that the next toy will take more than 15 minutes to assemble.
b) What is the probability that the next toy will take less than 8 minutes to assemble?
c) What is the probability that the next toy will take 10 to 16 minutes to assemble?
6. A student, working in a part time job, sells life insurance policies. The past data show that he (she) sells, on an average, 10 life insurance policies per 4-week period. Assume that the time between successive sales of life insurance policies by student has an exponential distribution.
a) What is the probability that the next life insurance policy will not be sold for two weeks?
b) What is the probability that the next life insurance policy will be sold within one week?
c) What is the probability that the next life insurance policy will sold in one to two weeks?
Answers
1. a) 0.0498; b) 0.9817; c) 0.1329; 2. 0.2725; 3. a) 0.1353; b) 0.2986;
4. a) 0.0369; b) 0.7275; 5. a) 0.2725; b) 0.5034; c) 0.1768; 6. a) 0.0067;
b) 0.9179; c) 0.0754.