4.4. The standard normal distribution

The standard normal distribution is a special case of the normal distribution. The particular normal distribution that has a mean of 0 and a standard deviation of 1 is called the standard normal distribution. It is customary to denote the standard normal variable by Z.

Definition:

The standard normal distribution has a bell-shaped density with

mean=

standard deviation=

The standard normal distribution is denoted by . (Fig.4.13)

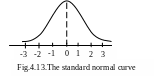
We will denote the cumulative distribution function of Z by F (z), and for two numbers a and b with a<b

Now let us see the procedure for finding probabilities associated with a continuous random variable. We wish to determine the probability of a random variable having a value in a specified interval from a to b. Thus we have to find the area under the curve in the interval from a to b. Finding areas under the standard normal distribution curve appears at first glance to be much more difficult. The mathematical technique for obtaining these areas is beyond the scope of the text, but fortunately tables are available which provide the areas or probability values for the standard normal distribution. The cumulative distribution function of the standard normal distribution is tabulated in Table 2 in the Appendix. This table gives values of

for nonnegative values of z.

For example the cumulative probability for a Z value of 1.13 from Table2

This is the area, shown in Figure 4.14, for Z less than 1.13.

Because of the symmetry of the normal distribution the probability that is also equal to 0.8708.

In general, values of the cumulative distribution function for negative values of z can be inferred using the symmetry of the probability density function.

T o find the cumulative probability for a negative z (for example Z=-2.25) defined as

We use the complement of the probability for as shown in

Figure 4.15.From the symmetry we can see that

We can see that the area under the curve to the left of is equal to the area to the right of because of the symmetry of the normal distribution.

Example: Find

Solution:

We see that because of the symmetry the probability or area to the right of

-1.35 (Fig.4.16) is the same as the area to the left of 1.35 (Fig.4.17.)

z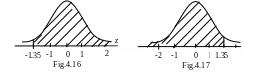

So,

.

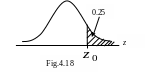
Example:

Let the random variable Z follow a standard normal distribution. The probability is 0.25 that Z is greater than what number?

Solution:

We need to find such a point that . (Fig.4.18)

Area to the left of is 1-0.25=0.75.

So,

and =0.675.

.

Exercises

1. Find the area under the standard normal curve to the left of

a) ; b) ;

c) ; d)

2. Find the area under the standard normal curve to the right of

a) ; b) ;

c) ; d) ;

3. Find the area under the standard normal curve over the interval

a) to ; b) to ;

c) to ; d) to ( interpolate)

4. For the random variable Z follows a standard distribution, find

a) ; b) ;

c) ; d) ;

e) ; f) ;

g) ; h) ;

i)

5. Find the z-value in each of the following cases:

a) ; b) ;

c) ; d)

6. Let the random variable Z follow a standard normal distribution.

a) The probability is 0.80 that Z is less than what number?

b) The probability is 0.35 that Z is less than what number?

c) The probability is 0.3 that Z is greater than what number?

d) The probability is 0.75 that Z is greater than what number?

Answers

1. a) 0.8790; b) 0.5636; c) 0.0336; d) 0.0107; 2. a) 0.1210; b) 0.2743;

c) 0.8708; d) 0.0606; 3. a) 0.4844; b) 0.7016; c) 0.3705; d) 0.6700;

4. a) 0.6628; b) 0.3372; c) 0.0455; d) 0.9545; e) 0.8670; f) 0.0966;

g) 0.2524; h) 0.9495; i) 0.1283; 5. a) -0.94; b) 0.84; c) 1.28 and -1.28;

d) 0.755; 6. a) 0.842; b) -0.386; c) 0.524; d) -0.675.