Розрахункові формули вдосконаленого методу Ейлера можна записати у вигляді

=y_k+ hf(x_k ,y_k) (7.9)

y_k+1=y_k+hf( , ) (7.10)

Отже, в удосконаленому методі Ейлера спочатку за методом Ейлера (формула (7.9)) обчислюють наближений розв'язок задачі (7.1)—(7.2) в точці =х_k+ , а потім за формулою (7.10) — наближений розв'язок y_k+1 у точці х_k+1; на кожному кроці інтегрування праву частину рівняння (7.1) обчислюють двічі (у точках (x_k, y_k) і ( , )).

Г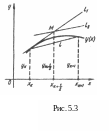 еометричне це означає, що на відрізку [x_k, х_k+1] графік інтегральної кривої задачі (7.1)—(7.2) замінюється відрізком прямої, яка проходить через точку (x_k, y_k) і має кутовий коефіцієнт k =f( ; ). Іншими словами, ця пряма (рис. 5.3) утворює з додатним напрямом осі Ох кут φ=arctgf( ; ).

Що ж до точки ( , ), то це точка перетину дотичної до інтегральної кривої задачі (7.1)—(7.2) в точці (x_k, y_k) з прямою х = x_k +h . Похибка вдосконаленого методу Ейлера на кожному кроці має порядок 0(h³).

Метод рунге—кутта

З появою і розвитком ЕОМ у чисельному інтегруванні звичайних диференціальних рівнянь бурхливого розвитку набули методи типу Рунге—Кутта. Такі методи побудовано до 10-го порядку точності включно. В обчислювальній практиці їх широко застосовують завдяки тому. що вони:

• однокрокові, тобто для обчислення розв'язку задачі (7.1)—(7.2) в точці х_k+1 треба знати її розв'язок лише в точці х_k

• дають змогу здійснювати чисельне інтегрування із змінним кроком;

• особливо зручні для програмування на ЕОМ. оскільки обчислення за ними має циклічний характер.

Поряд з перевагами ці методи мають і недоліки. Так, дуже важко оцінити похибки наближеного розв'язку задачі (7.1)—(7.2), бо відомі гарантовані оцінки локальної похибки здебільшого значно завищені, а тому практична їх цінність незначна. До недоліків слід віднести й те, що треба обчислювати в кількох точках праву частину рівняння (7.1) (функцію f(x,y)) на кожному кроці інтегрування. В удосконаленому методі на кожному кроці інтегрування значення функції f(x,y) обчислювали в двох точках, а в методах Рунге—Кутта третього і четвертого порядку точності його обчислюють відповідно в трьох і чотирьох точках. Що ж до методів Рунге-—Кутта, порядок точності яких більший від чотирьох, то праву частину рівняння (7.1) на кожному кроці інтегрування завжди обчислюють у точках, кількість яких більша від порядку точності методу. Уявлення про це дає табл. 5.1.

Табл. 5.1.

s	2	3	4	5	6	7	8	9	10
п	2	3	4,5	6	7,8	9	11	14	18

Тут s — порядок точності методу Рунге—Кутта, a n- кількість точок, в яких обчислюється функція f(x,y) на кожному кроці інтегрування.

Далі задачу Коші (7.1)—(7.2) розв'язуватимемо чисельно методами Рунге—Кутта, порядок точності яких не перевищує чотирьох. Припускатимемо, що функція f(х,у) в прямокутнику має неперервні частинні похідні до деякого порядку п. Тоді розв'язок у(х) матиме неперервні похідні до (n+1)-го порядку і для досить малих значень h у точці x_k+1=xk+ h, h > 0 його можна подати у вигляді розкладу

y(x_k+1)=y(x_k)+hy'(x_k)+ y"( )+…+ y⁽ⁿ⁾( )+O(hⁿ⁺¹). (7.11)

Похідні y⁽ⁱ⁾(x_k) (i= 1.2,....,n) у правій частині формули (7.11) можна виразити через значення функції f та її частинних похідних у точці ( , y_k).

Маємо

y'(x_k)=f( , y_k)=f _k (7.12)

y"(x_k) = f'_x.(x_k, y_k) + y' _kf'_y(x_k, y_k) = (f' _x + ff' _y)_k, (7.13)

де індекс k тут і далі означає, що відповідні функції обчислюють у точці ( , y_k).

Аналогічно обчислюють і похідні вищих порядків, хоч їх вирази із зростанням порядку значно ускладнюються. Тому безпосереднє використання їх для обчислення наближеного значення розв'язку У(x_k+1) =y(x_k + h) у точці x_k+1 за формулою (7.11) навряд чи може бути доцільним.

Слід зазначити, що для ЕОМ розроблено комплекси програм, які дають змогу машині самостійно виконувати формальне диференціювання функцій, якщо лише задано програму обчислення функції f(x,y). Таким чином, відпадає потреба створювати програми обчислення похідних функції f(x,y). Проте затрати машинного часу на виконання цих алгоритмів часто можуть бути такі великі, що доцільніше користуватися чисельними методами інтегрування звичайних диференціальних рівнянь, зокрема методами Рунге— Кутта.

Замість похідних y⁽ⁱ⁾_k (і=1.2....,n+1). що входять у праву частину формули (7.11), Рунге запропонував значення наближеного розв'язку y_k+1 в точці х_k+1 обчислювати за формулами вигляду:

y_k+1=y_k+ (7.14)

де функції k_i=hf(c_i,d_i) (i=1,2,…,n), c_i=x_k+a_ih, d_i=y_k+ , a w_i,a_i,(a₁=0) i β_ij- деякі сталі, які нaзивaтимемо параметрами формул Рунге-Кутта.

Невідомі параметри w_i, a_i, β_ij визначають з умови, щоб розклад за степенями h правої частини формули (7.14) збігався з розкладом (7.11) до якомога вищих степенів h для довільної функції f(х,у) і довільного кроку інтегрування h.

Перед побудовою розрахункових формул методів Рунге—Кутта введемо поняття порядку точності цих методів. Нехай у(х_k+1) = y(x_k+h) і у_k+1і — відповідно точний і наближений розв'язки задачі (7.1)—(7.2) в точці х_k+1, причому точний розв'язок обчислено за формулою (7.11), а наближений — за формулою (7.14), яку після розкладу за степенями h можна записати так:

y_k+1=y_k+ha₁+ a₂+ a₃+…+ a_n+1 (7.15)

де aі (і=1,2,...) — деякі числові коефіцієнти.

Найбільший з показників степеня h, при якому коефіцієнти розкладів (7.11) і (7.15) рівні між собою, називають порядком точності наближеного методу. Отже, якщо порядок точності наближеного методу дорівнює s, то це означає, що в розкладах (7.11) і (7.15) коефіцієнти a₁=y'_k, a₂= y''_k, аз = y'''_k,.... але а_s+1≠ y^(s+1)_k\

Зазначимо, що похибка методу на одному кроці інтегрування завжди має порядок на одиницю більший, ніж порядок точності методу. Тому порядок точності методу Ейлера дорівнює одиниці, бо похибка методу на одному кроці має порядок h², а порядок точності удосконаленого метода Ейлера дорівнює двом, бо порядок похибки цих методів на одному кроці h³.

Формули Рунге—Кутта першого порядку точності. Нехай функція f(x,y) в околі точки (x_k, y_k) має неперервні частинні похідні першого порядку. Тоді розв'язок у(х) задачі Коші в околі точки х_k матиме неперервні похідні до другого порядку включно. Тому для досить малих значень h у точці x_k+1= x _k+h його можна подати за степенями h, врахувавши (7.12), так:

У(х_k+1) = y(x_k)+hf(x_k,y_k) + 0(h²). (7.11)

формули Рунге—Кутта першого порядку точності будуватимемо в такому вигляді:

y_k+1=y_k+w₁k₁ (7.16)

де k₁ =hf(x_k,y_k), а w_i — невідомий параметр. Розклавши за степенями h праву частину виразу (7.16), матимемо

y_k+1=y_k+hf(x_k,y_k)w₁ (7.17)

Прирівнявши між собою коефіцієнти при h у формулах (7.11) і (7.17), знаходимо w_l=1. Підставивши це значення w₁ в рівність (7.16), впевнюємося в тому, що формулою Рунге—Кутта першого порядку точності (s=1) є формула Ейлера. Похибка цього методу y_k+1-y_k на кожному кроці є величиною порядку h².

Формули Рунге—Кутта другого порядку точності Нехай функція f(x у) в околі точки (х_k,y_k) має неперервні частинні похідні до другого порядку включно. Тоді розв'язок у(х) задачі Коші (7.1)-(7.2) в околі точки x_k матиме неперервні похідні до третього порядку включно. Тому для досить малих значень h у точці x_k+1= x _k+h його можна подати у вигляді такого розкладу за степенями h

y(x_k+1)=y(x_k)+hy'(x_k)+ y"( )+O(h³). (7.18)

Формули Рунге—Кутта другого порядку точності (s = 2) шукатимемо в такому вигляді:

y_k+1=y_k+w₁k₁ +w₂k₂ . (7.19)

де

k1=hf(xk,yk). (7.20)

k2= hf(xk+ a₂h, yk+β₂₁+k₁ ). (7.21)

a w₁,w₂,a₂ і β₂₁ — невідомі параметри, які визначають так, щоб (7.19) була формулою другого порядку точності (s =2), тобто, щоб коефіцієнти в розкладах (7.18) і (7.19) за степенями h були рівними між собою при h і h².

Функції k₁ і k₂ розкладають за степенями h так:

k₁=hfk

k₂ = hfk+a₂ h ² + h² β₂₁ + 0(h³).

Підставивши ці розклади k₁ і k₂ в (7.19), дістанемо розклад за степенями h (залишимо лише члени, пропорційні h²) виду:

y_k+1=y_k+h( w₁ +w₂) fk + h ² (w₂a₂ + w₂ β₂₁ )+ 0(h³). (7.22)

Прирівнявши коефіцієнти при hfk, h ² , h² у формулах (7.18) і (7.22), для визначення чотирьох невідомих параметрів w₁, w₂, a₂ і β₂₁ дістанемо алгебраїчну систему трьох рівнянь вигляду

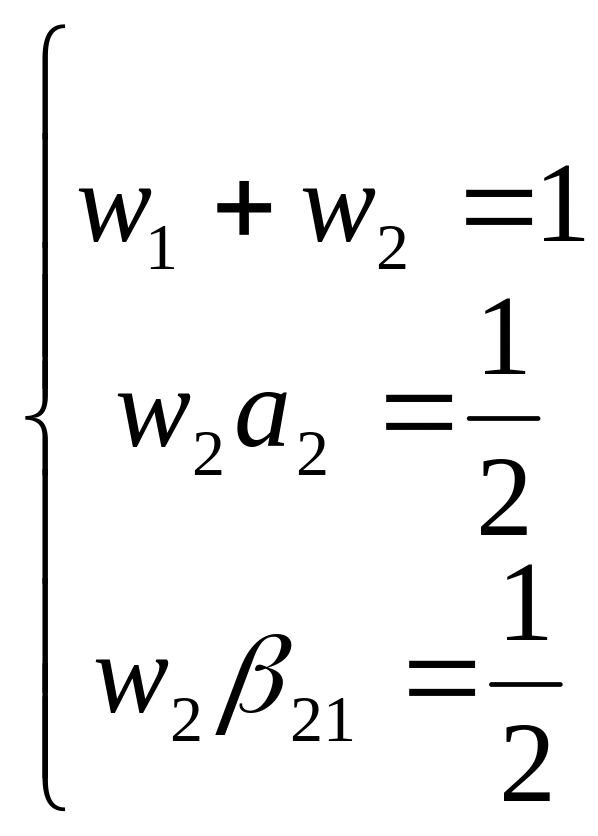(7.23)

З системи (7.23) видно, що w₂≠0, ₂≠0, β₂₁≠0 і ₂=β_21. Вона має нескінченну множину розв'язків, що залежить від одного параметра, причому кожний її розв'язок дає формули Рунге—Кутта другого порядку точності.

Якщо покласти w₂= , тоді w₁= , ₂=β₂₁= , а формули (7.19)-(7.21) набирають вигляду

y_k+1=y_k+ (k₁ +3k₂),

k₁=hf(x_k,y_k), k₂= hf(x_k+ h, y_k+ k₁ ).

Методи Рунге—Кутта четвертого порядку точності (s=4) можна побудувати аналогічно до попередніх, хоча це вимагатиме громіздкіших викладок і розв'язування нелінійної системи алгебраїчних рівнянь І складнішої структури. Похибка цих методів на кожному кроці інтегрування є величиною порядку h⁵. Самі формули мають вигляд

y_k+1=y_k+ (7.24)

Де

k₁ = hf(x_k, y_k),

k₂ = hf(x_k + a₂h, y_k + β₂₁k₁),

kз = hf(x_k + a₃h, y_k + β₃₁k₁+ β₃₂k₂), (7.25)

k₄= hf(x_k + a₄h,. y_k + β₄₁k₁+ β₄₂k₂+ β₄₃k₃).

До цих формул входять 13 невідомих параметрів w_i, a_i, β_ij .

Доведено, що існує нескінченна множина формул виду (7.24), (7.25), яка залежить від двох довільних дійсних параметрів і має четвертий порядок точності.

Обмежимось такими окремими прикладами формул, що належать до цієї множини:

1.

y_k+1=y_k+ (k₁ +2k₂+2k₃+k₄)) .

k₁=hf(x_k,y_k).

k₂= hf(x_k+ h, y_k+ k₁ ). (7.26)

k₃= hf(x_k+ h, y_k+ k₂ ).

k₄= hf(x_k+ h, y_k+k₃ ). .

Цю формулу найчастіше використовують в обчислювальній практиці. З геометричної точки зору формули (7.26) інтегральну криву задачі (7.1)-(7.2) на відрізку [x_k, x_k+1] замінюють відрізком прямої, яка проходить через точку (x_{k, ,}y_k) і утворює з додатним напрямом осі Ох кут .

На закінчення зазначимо, що розглянуті вище методи Рунге—Кутта застосовують також до нормальних систем диференціальних рівнянь першого порядку. Німецький математик Р.Цурмюль узагальнив методи Рунге—Кутта на випадок диференціальних рівнянь другого, третього і вищих порядків.