Розділ 7. ОБЧИСЛЮВАЛЬНІ МЕТОДИ РОЗВ’ЯЗКУ ЗВИЧАЙНИХ ДИФЕРЕНЦІЙНИХ РІВНЯНЬ.
ПОСТАНОВКА ЗАДАЧІ
Часто задачі техніки і природознавства математично зводяться до відшукання розв'язку певного диференціального рівняння (або системи таких рівнянь), який задовольняє певні початкові умови (задача Коші). Проінтегрувати таке рівняння в скінченному вигляді вдається досить рідко. При цьому дістають здебільшого такий вираз, до якого шукана функція входить неявне, а тому користуватися ним незручно.
На практиці застосовують здебільшого наближене інтегрування диференціальних рівнянь. Воно дає змогу знайти наближений розв'язок задачі Коші або у вигляді певного аналітичного виразу (наприклад, ряду Тейлора), або у вигляді деякої таблиці значень.
Розглянемо окремі методи чисельного розв'язування задачі Коші для звичайного диференціального рівняння першого порядку, розв'язаного відносно похідної. Наближений розв'язок задачі Коші записують у вигляді певної таблиці значень.
Задача Коші полягає в тому, щоб знайти розв'язок у(х) диференціального рівняння
У'=f(x,y), (7.1)
який задовольняє початкову умову
y(хо)=y0 (7.2)
Геометричне це означає, що треба знайти ту інтегральну криву у(х) рівняння (7.1), яка проходить через точку (xо, уо).
Задача Коші (7.1)—(7.2) має єдиний розв'язок, наприклад при виконанні умов такої теореми.
Теорема (Пікара). Якщо функція f(x,y) двох змінних х і у неперервна замкнутому прямокутнику
= {(х,
у): |х - хо
|≤l,
|у
- уо|
≤l}
з центром у точці (xо, Уо) і задовольняє в ньому умову Ліпниця по змінній у, тобто існує число К > 0, яке не залежить від х і у, таке, що
|f(х1,
У1)
-f(x2,
У2)
|
К|У1
– У2|
(7.3)
для будь-яких точок (х1,у1)Є і (x2,у2) Є , то існує єдина диференційовна функція у =φ(x), яка є розв'язком диференціального рівняння (7.1), що задовольняє початкову умову (7.2). Цей розв'язок визначений і неперервно диференційований принаймні на відрізку [x0-h;x0+ h],
де
h=min
, М
=
(7.4)
Розглянемо так звані однокрокові чисельні методи розв'язування задачі Коші (7.1)—(7.2), в яких, щоб знайти наближений розв'язок у точці x k+1 = xk +h, досить знати її розв'язок у точці хk. І оскільки розв'язок задачі в точці x0 відомий з початкових умов, то ці методи дають змогу обчислити послідовно значення розв'язку в наступних точках х1=x0+h, x2=x1+h, .... З однокрокових чисельних методів розглянемо лише явні методи Рунге—Кутта. Окремими представниками цих методів є методи типу Ейлера, які хронологічно передували методам Рунге—Кутта.
Надалі припускатимемо, що функція f(х,у) рівняння (7.1) задовольняє умови теореми Пікара.
Метод ейлера
Нехай на відрізку [хо; хо+l] треба знайти чисельний розв'язок задачі Коші (7.1)—(7.2). Для цього відрізок [хо; хо + l] поділимо на п (для простоти) рівних частин точками xo, x1, х2,..., хп = хо + l, де
xk=
хо +
kh (k =
0,1,2,...,
n), h=
.
Величину h називають кроком чисельного інтегрування диференціального рівняння (7.1).
Розв'язати задачу (7.1)—(7.2) чисельно — це означає для заданої послідовності xo, x1, х2,..., хп = хо + l, незалежної змінної х і числа у0 знайти числову послідовність у1, у2, ..., уп тобто для заданої послідовності значень незалежної змінної xk= хо + kh (k = 0,1,..., n) побудувати таблицю наближених значень шуканого розв'язку задачі Коші.
Якщо наближений розв'язок задачі (7.1)—(7.2) в точці хk відомий, то, проінтегрувавши рівняння (7.1) в межах від xk до хk+1, знайдемо його розв'язок в точці хk+1 за формулою
y(xk+1)=y(xk)+
.
(7.5)
Саме ця формула є вихідною для побудови багатьох чисельних методів розв'язування задачі (7.1)—(7.2).
Метод Ейлера. Якщо інтеграл у правій частині формули (7.5) обчислити за формулою лівих прямокутників, то знайдемо
y(xk+1)=y(xk)+hf(xk,y(xk)) + 0(h2). (7.6)
В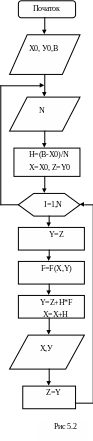
ідкинувши
в цій рівності доданок порядку 0(h2),
дістанемо розрахункову формулу
y(xk+1)=y(xk)+hf(xk,yk) (k = 0,1,2,..,n-l), h= xk+1-xk, (7.7)
яку називають формулою Ейлера. Тут і далі скрізь yk і y(xk) — відповідно наближене і точне значення шуканого розв'язку задачі (7.1)—(7.2) у точці xk. Різницю yk - y(xk)) називають похибкою наближеного значення yk в точці xk
Оскільки дотична до графіка функції у(х) в точці (xk,yk) має кутовий коефіцієнт k, який дорівнює значенню похідної y'k=f(xk,yk), то рівняння дотичної до інтегральної кривої у(х) задачі (7.1)—(7.2) в точці (xk,yk) матиме вигляд
у - yk = y'k(x -xk) або у- yk=f(xk, yk) (х - xk).
З
відси
для ординати точки уk+1
перетину цієї дотичної з прямою х
=
xk+1
дістанемо формулу (7.7). А це означає,
що на кожному з відрізків [xk
xk+1],
(k=0,1....,n-1)
інтегральна крива наближено замінюється
відрізком дотичної до неї в точці (xk,
yk).
Якщо в площині Оху
позначити точки Mk(xk;
yk), k =
0,1,2,....n
і сполучити їх по порядку відрізками,
то дістанемо ламану (її називають ломаною
Ейлера),
яка наближено зображує графік шуканого
розв'язку задачі (7.1)-(7.2). У цьому й полягає
геометричний зміст методу Ейлера (рис.
5.1).
Зазначимо, що похибка методу Ейлера
на кожному кроці є величина порядку
0(h2).
Точність методу досить мала і з переходом
від точки xk
до
точки
xk+1i.
її похибка систематично зростає.
Графічну схему алгоритму метода Ейлера подано на рис 5.2.
Удосконалений
метод Ейлера.
Якщо інтеграл у правій частині формули
(7.5) обчислити за формулою середніх
прямокутників, тобто значення
підінтегральної функції
f(x,y(x))
обчислити в точці
=xk+h/2
, то знайдемо
y(xk+1)=y(xk)+hf( ,y( )) + 0(h3)). (7.8)
Величину невідомого значення функції y( )) обчислимо за формулою (7.6) з кроком h/2. Матимемо
y(
)=y(xk)+
hf(xk,y(xk))
+ 0(h2)
Підставивши це значення у( ) в (7.8), дістанемо
y(xk+1)=y(xk)+hf(
,y(
)+
hf(xk
,y(xk))
+ 0(h2))+
0(h3)=
=y(xk)+hf( ,y( )+ hf( ,y(xk)) + 0(h3)
Відкинувши тут доданок, пропорційний h3, матимемо
yk+1=yk+hf(
,y
)+
hf(xk
,yk)