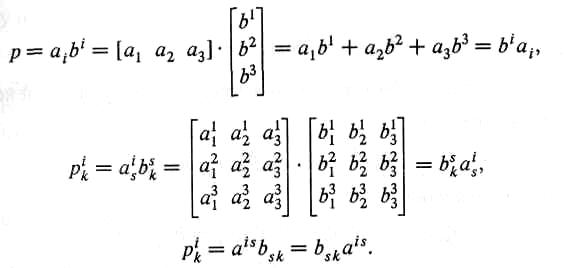Министерство образования и науки РФ

Пермский национальный исследовательский политехнический университет

Кафедра механики композиционных материалов и конструкций

Реферат

«Основные понятия и операции над тензорами

в трехмерном пространстве»

Выполнил: студент гр. ПКМ-08-2

Азанов А.О.

Проверил: зав. кафедры МКМК,

д. ф.-м. н., проф.

Соколкин Ю. В.

Пермь, 2011 г.

Понятия о тензорах различных рангов.

Введем в трехмерном пространстве прямоугольную декартову систему координат , c началом в точке O, тогда каждой точке пространства M будет взаимнооднозначно соответствовать радиус-вектор x с началом в точке O и концом в точке M. Выберем такой ортонормированный базис , у которого линия действия векторов совпадают с осями , а начало – с точкой O декартовой системы координат. Такой базис будем называть декартовым.

Трехмерное пространство, в котором существует единая для всех точек прямоугольная декартова система координат, называют трехмерным евклидовым.

Дадим теперь определение тензора произвольного ранга. Под тензором n-го ранга понимается 3ⁿ компонент ,которые при повороте системы координат определяются следующими соотношениями:

где - направляющие косинусы между новой и старой системой координат, , - компоненты тензора в новой и старой системе координат, соответственно.

Основные действия с объектами.

Рассмотрим два однотипных объекта. Элементы, имеющие один и тот же набор индексов в одинаковом размещении, назовем соответственными. Например, элементы и — соответственные, элементы и — не соответственные.

Равенство двух объектов определяется так же, как и раньше: равными называются два однотипных объекта, если все соответственные элементы попарно равны друг другу.

Если два объекта равны друг другу, например, , то же самое равенство можно записать при помощи любых других скользящих индексов, лишь бы они были одинаковы в обеих частях равенства

Равенства типа будем считать не имеющими смысла.

Объект называется нулевым, если все его элементы равны нулю. Поэтому равенство объекта нулю означает, что каждый из его элементов равен нулю.

Сложение определяется только для однотипных объектов, например:

Симметрия и антисимметрия. Понятие симметрии и антисимметрии вводится только для индексов, которые расположены или оба снизу, или оба сверху. Для индексов смешанного расположения эти понятия не вводятся.

Рассмотрим, для примера, объекты второго порядка . Если эти объекты таковы, что

то они называются симметричными. Наоборот, если имеют место равенства

то объекты называются антисимметричными.

Подобным же образом можно определить симметрию и антисимметрию для объектов любого строения и порядка выше двух; например, если для объекта верно равенство , то он называется симметричным по индексам к и l, а если , то антисимметричным по индексам к и l.

Симметрирование и альтернирование. Если объект имеет два одинаково расположенных индекса (т. е. оба внизу или оба вверху), то его всегда можно разложить на сумму двух слагаемых, из которых одно симметрично по рассматриваемым двум индексам, другое - антисимметрично, например:

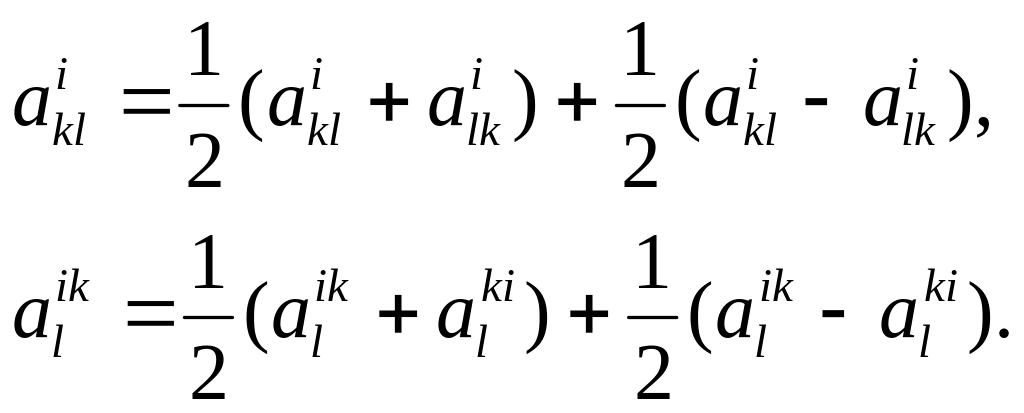
Введя обозначение

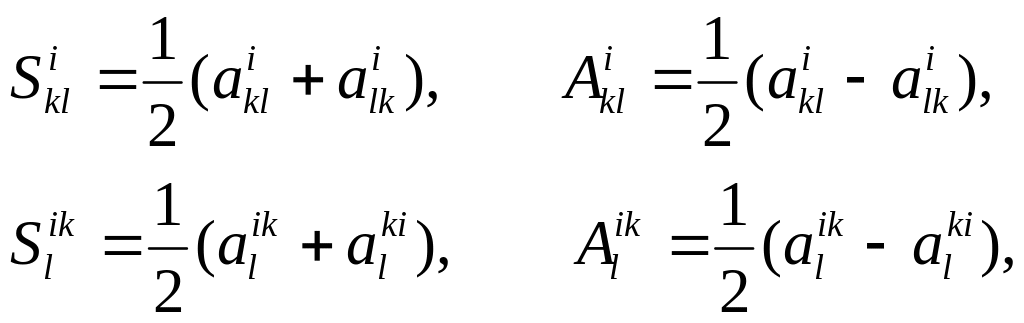
мы можем написать

Операция выделения из объекта его части, симметричной по каким-нибудь двум индексам или антисимметричной по ним, называется соответственно симметрированием и альтернированием.

Свертка (условие о суммировании). Обычно условие о суммировании вводится в виде, предложенном Эйнштейном: суммирование производится только в том случае, если одинаковы один верхний и один нижний скользящий индексы, например:

Однако, мы наравне с этим будем применять условие о суммировании в старой форме, т. е. будем суммировать также и по двум повторяющимся нижним скользящим индексам. Будут встречаться случаи суммирования и по верхним повторяющимся индексам.

Поэтому мы введем условие о суммировании в следующей форме: суммирование производится по любым двум повторяющимся скользящим индексам, независимо от их расположения.

Однако свертки объектов по двум верхним или двум нижним индексам будут нам встречаться довольно редко; как правило, мы будем пользоваться сверткой в смысле Эйнштейна.

Отметим сразу же, что введенное таким образом условие о суммировании по двум верхним или двум нижним индексам есть чисто вычислительный прием. Как будет показано в дальнейшем, свертка тензора по двум верхним или двум нижним значкам не приводит к новому тензору, т. е. не является тензорной операцией. Наоборот, условие о суммировании в смысле Эйнштейна всегда приводит к новым тензорам.

Разумеется, немой индекс можно по-прежнему обозначать любой буквой, но так, чтобы избежать его повторения больше чем два раза.

Обобщенное умножение определим только для объектов одинакового числа измерений, порядок и строение которых произвольны. Мы имеем, например:

и т.д., откуда ясно правило индексов для произведения: ему нужно приписать сверху и снизу индексы, одинаковые в обеих частях равенства. Таким образом, здесь уже нет полной свободы в размещении индексов у обобщенного произведения, которой мы могли пользоваться, когда рассматривали только одни объекты нижнего строения.

Обобщенное произведение коммутативно относительно сомножителей, но не коммутативно относительно их индексов, например:

В последнем примере нельзя написать или , потому что такая запись противоречит только что установленному правилу о размещении индексов в обобщенном произведении.

Частным случаем обобщенного умножения со сверткой является матричное умножение: