2.6. Синтез кривошипно-коромысловых механизмов

Кривошипно-коромысловые механизмы служат для преобразования вращательного движения кривошипа во вращательное (качательное) движения коромысла.

2.6.1. Синтез шарнирного четырехзвенника по трем положениям входного и выходного звеньев

Пример 2.1

Определить длины звеньев шарнирного четырехзвенника (l_1, l_2, l_3, l₀) по трем положениям входного звена (углы φ_1, φ_2, φ₃) и соответствующим им трем положениям выходного звена (углы ψ_1, ψ_2, ψ₃ ) (рисунок 2.7).

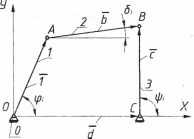
Рисунок 2.7-Шарнирный четырехзвенник

Решение:

Эту задачу удобно решать в относительных единицах, т.е

l₁/l₁=1, l₂/l₁=b, l₃/l₁=c, l₄/l₁=d. (2.15)

Тогда число независимых параметров, подлежащих определению, равно трем (b, с, d). Так как для заданного механизма можно составить три уравнения, связывающие углы, характеризующие положения входного и выходного звеньев, то задача синтеза будет иметь точное решение.

Стороны рассматриваемого шарнирного четырехзвенника представим векторами l , b, с, d (рисунок 2.7). Тогда векторное уравнение условия замкнутости можно записать так: l+b=c+d, (2.16)

Уравнения проекций на оси координат для произвольного положения механизма имеют вид:

cosφ_i + b∙cosδ_i = c∙cosψ_i + d (2.17)

sinφ_i + b∙sinδ_i = c∙sinψ_i (2.18)

или

b∙cosδ_i = c∙cosψ_i + d – cosφ_i (2.19)

b∙sinδ_i = c∙sinψ_i - sinφ_i. (2.20)

Здесь угол δ₁ - угол, образованный шатуном с осью X, неизвестен. Возводя левые и правые части в уравнения (2.19) и (2.20) в квадрат и складывая полученные равенства, получим:

b²=d²+c²+1+2cd∙ cosψ_i-2d∙ cosφ_i-2c∙cos(ψ_i – φ_i)

отсюда

d²+c²+1-b² c

cosφ_i= ———— + c∙cosψ_i -- — ∙ cos(ψ_i – φ_i). (2.21)

2d d

Введем обозначения:

d²+c²+1-b²

p₁=c, p₂= -c/d, p₃= ———— . (2.22)

2d

Тогда

p₁∙cosψ_i+ p₂∙cos(ψ_i – φ_i)+ p₃- cosφ_i=0. (2.23)

Подставив в уравнение (2.22) заданные углы φ_1, φ_2, φ₃ и ψ_1, ψ_2, ψ_3, получим систему из трех линейных уравнений:

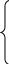p₁∙cosψ₁+ p₂∙cos(ψ₁ – φ₁)+ p₃- cosφ₁=0

p₁∙cosψ₂+ p₂∙cos(ψ₂ – φ₂)+ p₃- cosφ₂=0. (2.24)

p₁∙cosψ₃+ p₂∙cos(ψ₃ – φ₃)+ p₃- cosφ_i=0.

Решая систему (2.24),найдем Р_1, Р₂, Рз, а затем по формулам (2.23) параметры b, с, d. Выбрав величину l₁ по уравнениям (2.1) определим длины звеньев 1₂, l₃, l₀.

2.6.2. Синтез шарнирного четырехзвенника по заданному коэффициенту изменения скорости

Пример 2.3

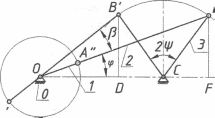
Рисунок 2.8 - Шарнирный четырехзвениик

Дано:

R - длина коромысла;

ВС, 2ψ - угол качания коромысла, симметричный относительно перпендикуляра к стойке ОС;

К – коэффициент изменения средней скорости выходного звена;

Определить: г - длину кривошипа 1,1- длину шатуна 2,L- длину стойки

OC.

Решение:

Неизвестные длины звеньев кривошипно-коромыслового механизма определяем, исходя из крайних положений механизма. Угол р между крайними положениями шатуна определяем по формуле: β=180˚∙(К-1) / (К+1).

Точка D и F являются проекциями точек В’ и B” на стойку.

Из ∆CB’D и ∆OB’D следует, что B’D=R∙ cosψ, DC=R∙sinψ_,

B’D 1

—— = ————

OD tg(β+ φ)

или

L-R∙sinψ 1

———— = ———— (2.25)

R∙ cosψ tg(β+ φ)

Из ∆CB”F и ∆OB”F получим, что CF = R∙sinψ , B”F = R∙ cosψ ,

OF L+R∙sinψ

—— = ————

FB” R∙ cosψ

или

L+R∙sinψ 1

———— = —— . (2.26)

R∙ cosψ tgφ

Выражения (2.25) и (2.26) приведем к виду:

L 1 L 1

———— - tgψ = ——— , ———— + tgψ = ——— .

R∙ cosψ tg(β+ φ) R∙ cosψ tgφ

Решая совместно уравнения (2.25) и (2.26), получим:

1 1

— - ——— = 2∙tgψ

tgφ tg(β+φ)

или

1 1 - tgφ∙tgβ

—— = ————— = 2∙tgψ , (2.27)

tgφ tgφ + tgφ

откуда

- tg ψ ∙ tgβ ± √tg² ψ∙ tg² β – (tgψ – tgβ)∙ tgβ

tgφ = ————————————————— (2.28)

2∙ tgψ – tgβ

Подставляя в уравнение (2.28) значения углов β и ψ и выбирая из двух значений тангенса положительное, определим угол φ, по которому из уравнения (2.26) найдем:

cosψ - tgφ∙sinψ

L = R∙ ——————— . (2.29)

tgφ

Тогда из ∆OB’D

B’D Rcosψ OB’ = l – r = ———— = ———— . (2.30)

sin(φ+β) sin(φ+β)

B”D Rcosψ

OB” = l+r = ——— = ——— (2.31)

sinφ sinφ

просуммируем правые и левые части уравнений (2.30) и (2.31), определим:

Rcosψ Rcosψ

2l = ———— + ——— ,

sin(φ+β) sinφ

откуда

Rcosψ(sinφ + sin(φ+β))

l = —————————— . (2.32)

2 ∙sinφ∙ sin(φ+β)

Вычитая из равенства (2.31) равенство (2.30) определим:

Rcosψ Rcosψ

2r = ——— - ———,

sinφ sin(φ+β)

Тогда

sin(φ+β) - sinφ

r = R∙cosψ ∙ ——————— . (2.33)

2∙ sinφ∙ sin(φ+β)