ЛАБОРАТОРНАЯ РАБОТА № 1

ИССЛЕДОВАНИЕ ТОЧНОСТИ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА МЕХАНИЧЕСКОЙ ОБРАБОТКИ ДЕТАЛЕЙ СТАТИСТИЧЕСКИМ МЕТОДОМ

1.1 Статистические методы исследования точности обработки

При анализе точности технологического процесса приходится рассматривать как систематические, так и случайные погрешности обработки.

Исследование случайных погрешностей основывается на выводах теории вероятностей и математической статистики. При изучении случайных погрешностей изготовления удобно пользоваться кривыми распределения, которые строятся на основании многократных наблюдений одного и того же явления. По эмпирическим кривым распределения можно в первом приближении оценить, какому из известных законов распределения ближе всего соответствует распределение исследуемой случайной погрешности.

Как показали многочисленные исследования, распределение погрешностей при обработке деталей на станках ближе всего соответствуют закону нормального распределения (закону Гаусса).

Для непрерывных случайных величин уравнение кривой нормального распределения выражается в следующем виде:

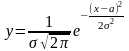, (1.1)

где σ - среднее квадратичное отклонение;

a - истинное среднее значение случайной величины;

e - основание натуральных логарифмов;

x - аргумент функции плотности вероятности, т.е. случайная величина,-∞<x< ∞.

Постоянные величины а и σ называются параметрами распределения.

Истинное среднее значение случайной величины (математическое ожидание Mx) определяет центр группирования случайной величины.

Для непрерывных случайных величин

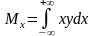, (1.2)

Другой параметр распределения - среднее квадратическое отклонение - характеризует рассеяние случайной величины

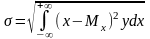, (1.3)

Рассеяние случайных величин характеризуется также дисперсией

.

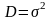Для закона нормального распределения может быть рассчитана вероятность попадания случайной величины в пределы любого из выбранных интервалов

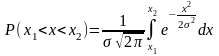(1.4)

Так, например, для интервала х=±3σ вероятность попадания случайной величины равна 0,9973 (99,73%), т.е. очень близка к единице (100%). Поэтому при практических расчетах точности обработки пределы изменения случайной величины ±3σ обычно принимают за величину полной случайной погрешности. Таким образом, теоретически значение случайной величины (погрешности) может быть рассчитано аналитическим путем.

При экспериментальных исследованиях, когда число опытов ограничено, аналитически рассчитать величину случайной погрешности не представляется возможным, поэтому определяются ее приближенные значения, а именно:

среднее арифметическое значение случайной погрешности

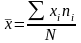, (1.5)

где хi - среднее значение интервала;

ni - количество размеров в интервале.

Эмпирическое среднее квадратическое отклонение

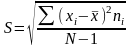при N≤30, (1.6)

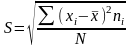при N>30, (1.7)

где N - объем выработки, который должен определяться в соответствии с рекомендациями ГОСТ 16467 - 70.

Для оценки характеристики рассеяния параметров точности обработанной парии деталей строится эмпирическая кривая распределения. Построение этой кривой начинается с измерения требуемых параметров качества деталей выбранной партии, например, точности размеров детали. Расположив полученные действительные размеры Ai в порядке возрастания их значения, получим ряд случайных дискретных величин (табл. 1.1). Разность между Amax и Amin определит поле рассеяния ω (или величину размаха R по ГОСТ 15893-77).

ω=Amax-Amin (1.8)

Полученная величина поля рассеяния ω делится на несколько интервалов ΔX (7+15) с тем расчетом, чтобы в каждый интервал попало достаточное количество измерений. Далее определяется частотность попадания размеров в каждый интервал

, (1.9)

где ni - количество размеров, попавших в i - тый интервал;

N - общее число деталей.

На основании результатов измерений и расчетов составляется таблица 1.2, которую графически можно представить в виде гистограммы или кривой распределения (рис.1).

По формулам (1.5) - (1.7) определяются основные характеристики эмпирической кривой распределения.

При исследовании случайных погрешностей необходимо оценить, в какой мере результаты экспериментального исследования отвечают закону нормального распределения. В первом приближении качественная оценка степени соответствия эмпирического распределения закону нормального распределения может быть произведена по внешнему виду эмпирической кривой.

Визуально сравнительную оценку удобно проводить, используя совмещенные графики эмпирического и теоретического распределения построенные в одном масштабе.

Теоретическая частота n'i определяется по формуле

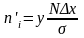, (1.10)

где ,

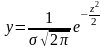где 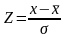независимая переменная.

При σ=1 значения " y " табулированы:

±Z	0	0,5	1,0	1,5	2,0	2,5	3
±Y	0,40	0,35	0,24	0,13	0,05	0,02	0,004

При построении кривой нормального распределения принимаем σ≈S, тогда

(1.11)

Практически для построения кривой нормального распределения достаточно определить координаты шести-семи точек, в том числе четырех характерных точек. Одна из характерных точек, соответствующая абсциссе x=x, является вершиной кривой, а остальные три берут с абсциссами x=S, x=2S и x=3S. При этом

,

, .

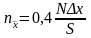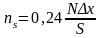
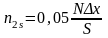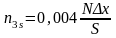Максимальное несовпадение кривых распределения ∆nmax (рис. 1.1) не более 10% считается удовлетворительным.

Оценка точности обработки партии деталей по характеристикам распределения действительных размеров производится путем сравнения величины рассеяния этих размеров с расчетным допуском TAi.

Если закон распределения отклонений размеров выбранной партии деталей подчиняется нормальному распределению, то вероятность P выхода числа обрабатываемых деталей за установленное поле допуска TAi можно рассчитать по уравнению

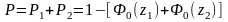, (1.12)

Где Ф0(z) – нормированная функция Лапласа с аргументами Z1 и Z2,

, .

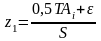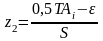- смещение середины поля допуска относительно центра группирования;

Am - размер детали, соответствующий середине поля допуска (рис.1.1).