3.1.2. Прямое произведение графов

Прямым произведением графов и называется граф, у которого (т.е. вершины имеют вид где причём

(3)

соединены ребром в точности в следующих случаях: а) б)

Например, если то графом будет являться треугольная призма (см. рис. 3.5).

Для графического построения графа следует нарисовать граф а затем каждую из вершин “раздуть” до графа

Упражнение 3.5. Изобразить граф

Решение (см. рис. 3.6).

Н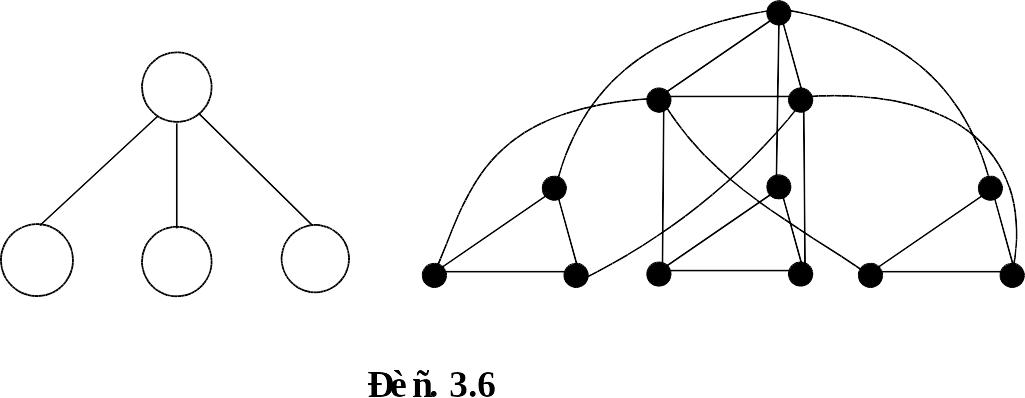 арисуем граф с вершинами большого размера – для того, чтобы заменить каждую из них графом Соединение вершин осуществляется по правилу (3).

Граф (п-мерный куб). Его вершинами являются строчки где или 1. Две вершины и соединены ребром в том и только том случае, если строчки и имеют отличие ровно в одной позиции, т.е. существует такое что и при На рисунке 3.7 изображены графы и

Для упрощения обозначений в записи вершин мы не пишем скобки и запятые, т.е. пишем 110 вместо

Упражнение 3.6. Найти количество вершин и рёбер графа

Решение. Так как вершины графа – это строчки и то всего вершин Далее, для вершины можно получить смежных с ней вершин, меняя поочерёдно каждую компоненту на противоположную Следовательно, из каждой вершины исходит ровно рёбер. Значит, общее количество рёбер равно (деление на 2 делается ввиду того, что иначе каждое ребро было бы подсчитано дважды). Итак,

3.1.3. Подграф. Связный граф. Компоненты связности графа

Пусть – граф. Понятие подграфа имеет два различных не эквивалентных между собой определения.

Подграф в широком смысле графа – это граф где

Подграф в узком смысле – это граф где и

И ными словами, для построения у графа подграфа в широком смысле надо выделить какое-либо множество вершин и некоторые из них соединить рёбрами, взятыми из графа Для получения подграфа в узком смысле надо взять какое-либо множество вершин и соединить их в точности теми рёбрами, которыми они соединялись в графе На рисунке 8 изображены графы и такие, что – подграф графа в широком, но не в узком смысле. Чтобы получить из него подграф в узком смысле, следует добавить ребро

Далее словом “подграф” мы будем называть подграф в широком смысле.

Граф называется связным, если для любых двух его вершин и существует путь из в Будем считать, что из в всегда существует путь нулевой длины (если длину определять по количеству рёбер). Любой граф является объединением своих связных подграфов таких, что не существует рёбер (а значит, и путей), соединяющих вершины из разных Эти подграфы называются компонентами связности графа

Н апример, граф изображённый на рисунке 3.9, состоит из трёх компонент связности.

У связного графа

3.1.4. Матрица смежности и матрица инцидентности графа

Пусть дан граф с множеством вершин и множеством рёбер

Матрица смежности графа – это матрица размера элементы которой определяются по формуле

Матрица инцидентности графа – это матрица размера элементы которой определяются по формуле

Следует отметить, что каждая из матриц определяет граф однозначно (с точностью до изоморфизма): графы, имеющие одинаковые матрицы (или изоморфны друг другу. Далее, перестановка строк или столбцов матрицы даёт граф, изоморфный первоначальному (это соответствует перенумерации вершин или рёбер графа ). Матрица симметрическая (т.е. или, другими словами, при любых ). На диагонали матрицы стоят нули ( ). Перестановка строк или столбцов матрицы вообще говоря, недопустима. Однако, можно делать синхронные перестановки строк и столбцов с одинаковыми номерами, т.е. переставлять между собой i-ю и j-ю строки, затем i-й и j-й столбец и т.д. – это соответствует перенумерации вершин графа.

Замечание. Для обобщённых графов (графов с петлями или кратными рёбрами) и для ориентированных графов также можно ввести понятие матрицы смежности и матрицы инцидентности. Тогда в матрице смежности могут появиться (у графов с кратными рёбрами), на диагонали могут быть элементы (у графов с петлями), у ориентированного графа матрица может не быть симметрической.

Упражнение 3.7. Построить матрицу смежности и матрицу инцидентности графа изображённого на рисунке 3.10.

Решение. Пусть вершины и рёбра занумерованы так, как показано на рисунке. Тогда по определению матриц и получаем:

Можно заметить, что в каждой строке матрицы стоят ровно две единицы. Это общий факт, справедливый для любого графа. Он следует из того, что каждое ребро инцидентно ровно двум вершинам.

Отметим ещё ряд свойств матриц и Количество единиц в i-й строке матрицы (или, что то же самое, сумма элементов i-й строки) равна степени вершины:

Кроме того, как уже отмечалось ранее,

Двойные суммы сводятся к однократным следующим образом: Поэтому а значит,

(4)

Аналогично получаем, что

Упражнение 3.8. Построить граф по его матрице смежности

Р ешение. Так как а остальные равны 0, то рёбрами соединяются лишь пары вершин 1-2 и 3-4. Мы получаем граф, изображённый на рисунке 3.11.

Этот граф несвязный, он имеет две компоненты связности: одна с вершинами 1, 2, другая – с вершинами 3, 4.

У пражнение 3.9. Изобразить граф, имеющий следующую матрицу инцидентности:

Решение. По матрице мы определяем, что граф имеет 5 вершин и 4 ребра. Так как в 1-й строке матрицы единицы стоят на 1-й и 5-й позициях, то ребро соединяет вершины 1 и 5. Рассматривая остальные строки матрицы и рассуждая аналогично, мы получим граф, изображённый на рисунке 3.12.

Упражнение 3.10. Выяснить, существует ли граф со следующим набором степеней вершин:

(а) 1, 1, 1, 2, 2, 3, 3, 4; (б) 1, 1, 1, 2, 2, 2, 3, 4.

Решение. По формуле (4) т.е. Это невозможно, так как Р – целое число. Следовательно, графа с набором степеней вершин (а) не существует.

Для набора (б) получаем поэтому можно попробовать построить граф. Начинать, конечно, нужно с вершины степени 4, затем подрисовывать вершины и рёбра. Вершин должно быть 8, так как даны 8 степеней вершин. Попытки построить граф оказываются успешными, более того, найдены даже два таких графа: и – см. рис. 3.13. Графы и не изоморфны, например, ввиду того, что у графа вершина степени 3 инцидентна двум вершинам степени 1, а в графе это не так.

Замечание. Предыдущее упражнение показывает, что набор степеней вершин не определяет граф однозначно.

Упражнение 3.11. Доказать, что в любом графе, содержащем более одной вершины, найдутся две различные вершины одинаковой степени.

Решение. Пусть – граф с вершинами. Тогда степени вершин могут принимать значения Этих чисел штук. Если все степени вершин различны, то для каждого существует вершина степени Значит, есть вершина степени 0 и есть вершина степени Так как то – изолированная вершина, она не соединена ребром ни с какой вершиной. А так как то вершина соединена со всеми остальными вершинами и, в частности, с вершиной Мы получили противоречие, а значит, графа с различными степенями всех вершин не существует.

Возникает естественный вопрос: как по матрице смежности или матрице инцидентности графа определить, является ли граф связным, и разбить его на компоненты связности? Ответ получить несложно: если матрицу синхронной перестановкой строк и столбцов можно превратить в блочную матрицу:

где – квадратные матрицы, то граф несвязен. При этом блоки и являются матрицами смежности двух непересекающихся подграфов графа таких, что Продолжая делать синхронные перестановки строк и столбцов, мы в конце концов получим:

где – квадратные матрицы, которые уже нельзя разложить на блоки (синхронной перестановкой строк и столбцов). В этом случае – матрицы смежности подграфов и – разложение графа на компоненты связности.

Приведём пример. Пусть

–

матрица инцидентности графа Поставим второй и третий столбцы в конец матрицы, а затем то же сделаем со второй и третьей строками. Мы получим:

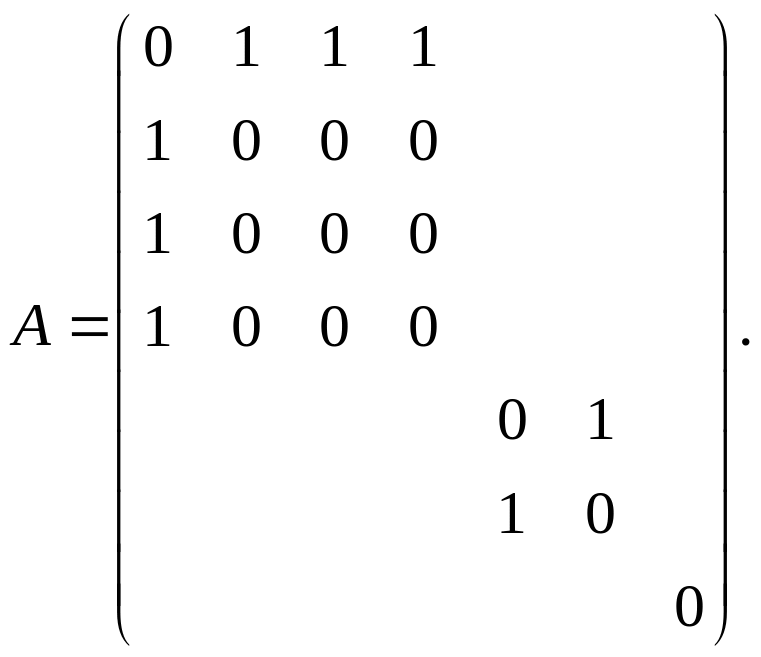
Незаполненные участки матрицы состоят из нулей. Мы их не пишем, чтобы подчеркнуть блочный вид матрицы. Теперь ясно, что граф состоит из 3 компонент связности (см. рис. 3.14).

Нумерация вершин на рисунке 3.14а соответствует новой матрице. На рисунке 14б приведён граф с первоначальной нумерацией вершин. Связь между двумя нумерациями видна из следующего преобразования: (столбцы и строки с номерами 2,3 отправляются в конец).

Степени матрицы смежности ( ) имеют интересный геометрический смысл. А именно, пусть Тогда равно количеству путей длины (т.е. из рёбер) из i-й вершины в j-ю. Приведём пример. Матрица является матрицей смежности графа изображённого на рисунке 3.15.

В озведём матрицу в квадрат. Получим: Так как то существуют ровно 2 пути длины 2 из вершины 2 в эту же вершину. Это 2-1-2 и 2-3-2.