§ 2.3. Минимизация булевых функций в классе днф

Пусть задан алфавит переменных .

Определение. Формулу вида ( при , ) называют элементарной конъюнкцией ранга r над множеством X. Константа 1 рассматривается как элементарная конъюнкция ранга 0.

Например, формула - элементарная конъюнкция ранга 3 над множеством ; в то время как формула элементарной конъюнкцией не является.

Упражнение 2.22. а) Перечислите все элементарные конъюнкции ранга 3 над множеством , обращающиеся в единицу на наборе .

б) Перечислите все элементарные конъюнкции над множеством , обращающиеся в единицу на наборе .

◄ а) , , , ; б) , , , , , , ,1.►

Определение. Формулу вида ( при ), где через обозначены элементарные конъюнкции над множеством X, называют дизъюнктивной нормальной формой (ДНФ) над множеством X. Сумма рангов конъюнкций, входящих в ДНФ, называется сложностью ДНФ.

Например, - ДНФ сложности 6; - ДНФ сложности 4; - ДНФ сложности 3 над множеством .

Заметим, что формулы равносильны и, следовательно, реализуют одну и ту же функцию h. Делаем вывод: функция может быть реализована в виде ДНФ не единственным образом, причем ДНФ, реализующие функцию, могут иметь различную сложность.

Определение. ДНФ, имеющая по сравнению с другими ДНФ, реализующими данную функцию, наименьшую сложность, называется минимальной дизъюнктивной нормальной формой данной функции.

Так, для функции h (см. выше), реализуемой дизъюнктивными нормальными формами , , дизъюнктивная нормальная форма является минимальной, поскольку h зависит от переменных существенным образом и, значит, не может быть представлена ДНФ, содержащей менее трех букв.

Поставим задачу: построить для произвольной булевой функции минимальные ДНФ.

Заметим, что у этой задачи существует тривиальное решение. Дадим его пошаговое описание.

1. Строим все ДНФ над множеством . Их 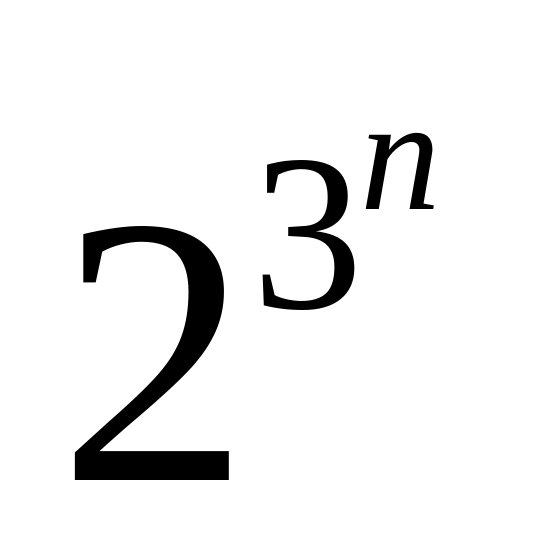. Действительно, число различных элементарных конъюнкций равно 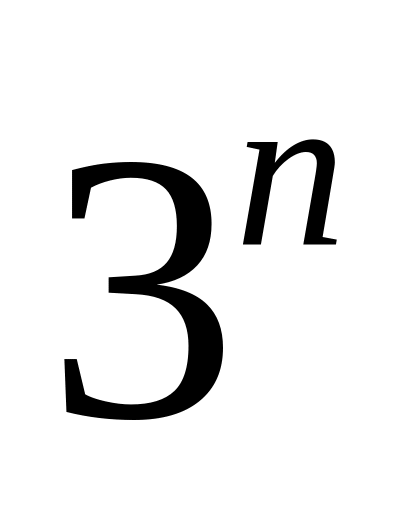, так как для каждой переменной имеется три возможности: присутствовать в конъюнкции, присутствовать с отрицанием и отсутствовать («пустой» конъюнкции сопоставлена константа 1). Каждая из конъюнкций, в свою очередь, может либо входить, либо не входить в ДНФ.

2. Отбираем из построенных ДНФ те, которые реализуют функцию .

3. Для отобранных ДНФ определяем сложности; ДНФ наименьшей сложности и есть искомые минимальные ДНФ функции .

В силу большого объема операций пользоваться изложенным выше алгоритмом практически невозможно. Разработано несколько экономичных методов построения минимальных ДНФ. Мы познакомимся с одним из них.

Выбранная нами для изучения методика построения минимальных ДНФ оперирует с несколькими видами дизъюнктивных нормальных форм. С двумя из них мы уже знакомы – это совершенная и минимальная дизъюнктивные нормальные формы. Рассмотрим еще две - сокращенную и тупиковую дизъюнктивные нормальные формы. Предварительно введем ряд новых понятий.

Определение. Элементарная конъюнкция называется импликантой функции , если на любом наборе , на котором эта элементарная конъюнкция равна 1, функция также обращается в 1.

Очевидно, что каждая элементарная конъюнкция любой ДНФ, реализующей функцию , является ее импликантой.

Определение. Будем называть импликанту функции ее простой импликантой, если элементарная конъюнкция, получающаяся из нее удалением любой буквы, уже не является импликантой .

Упражнение 2.23. Перечислить все простые импликанты функции:

а) ; б) .

◄ а) Имеем 9 элементарных конъюнкций над переменными : 1, , , , , , , , . Посмотрим, какие из них являются простыми импликантами функции .

0	0	1
0	1	1
1	0	0
1	1	1

Константа 1 импликантой не является, так как на любом булевом векторе равна 1, в то время как .

обращается в 1 на наборах и , а , следовательно, не является импликантой .

обращается в 1 на наборах , , и на каждом из этих наборов также равна 1, следовательно, – импликанта . Эта импликанта простая, так как конъюнкция 1, полученная из нее путем удаления , импликантой не является.

обращается в 1 на наборах , , и на каждом из этих наборов также равна 1, следовательно, – импликанта . Эта импликанта простая, так как конъюнкция 1, полученная из нее путем удаления , импликантой не является.

обращается в 1 на наборах и , а , следовательно, не является импликантой .

обращается в 1 на одном наборе , и , следовательно, – импликанта . Однако простой эта импликанта не является, так как конъюнкция , полученная из нее путем удаления буквы , является импликантой.

обращается в 1 на одном наборе и , следовательно, – импликанта . Однако простой эта импликанта не является, поскольку конъюнкции и , полученные из нее путем удаления буквы , являются импликантами.

обращается в 1 на наборе , а , следовательно, не является импликантой .

обращается в 1 на наборе , , следовательно, импликанта . Однако простой эта импликанта не является, так как конъюнкция , полученная из нее путем удаления , является импликантой.

Таким образом, функция имеет две простых импликанты и .

б) решите самостоятельно. ►

Определение. Дизъюнкция всех простых импликант функции называется сокращенной ДНФ функции.

Например, для функции (упр. 2.23 а)) сокращенная ДНФ имеет вид .

Можно доказать, что сокращенная ДНФ функции реализует функцию . Более того, в некоторых случаях функцию реализует дизъюнкция только некоторых (не всех!) простых импликант. В связи с этим уместно ввести понятие тупиковой ДНФ.

Определение. Тупиковой ДНФ функции называется такая реализующая ее дизъюнкция простых импликант, из которой нельзя удалить ни одну простую импликанту так, чтобы полученная после удаления ДНФ все еще реализовала функцию.

Отметим без доказательства следующий теоретический факт: минимальная ДНФ функции является тупиковой ДНФ.

Теперь, когда все необходимые понятия введены, мы можем наметить план построения минимальной ДНФ функции. План будет включать три этапа: на первом этапе строится сокращенная ДНФ функции, на втором – тупиковые ДНФ, на третьем – из тупиковых отбираются минимальные.

1-ый этап. Получение сокращенной ДНФ функции.

Далее будем использовать следующие равносильные преобразования:

а) операцию неполного склеивания, которая состоит в замене выражения на ;

б) операцию полного склеивания, которая состоит в замене выражения на ;

в) операцию поглощения, которая состоит в замене выражения на .

Для построения сокращенной ДНФ воспользуемся методом Квайна, который состоит в следующем:

0-ой шаг. Строится СДНФ функции.

1-ый шаг. а) К каждой паре конъюнкций из СДНФ применяется, если это возможно, операция неполного склеивания ( заменяется на ).

б) С помощью операции поглощения удаляются те конъюнкции ранга n, которые можно удалить таким образом. Убираются дублирующие члены . В итоге получается некоторая ДНФ .

(k +1)-ый шаг. Пусть после k ( ) этапов построена ДНФ . К каждой паре конъюнкций ранга ДНФ применяются операции неполного склеивания и поглощения и убираются дублируемые члены. В результате получается ДНФ .

Алгоритм завершается, если .

В качестве примера построим методом Квайна сокращенную ДНФ функции .

.

2-ой этап: построение тупиковых ДНФ.

На 1-ом этапе мы построили сокращенную ДНФ и, значит, нашли совокупность всех простых импликант функции. Тупиковые ДНФ можно строить, исходя из этой совокупности.

Будем действовать по следующему алгоритму. Пусть - произвольная булева функция. Назовем носителем функции множество булевых векторов, на которых функция принимает значение 1. Пусть булевы векторы - элементы носителя функции , - совокупность простых импликант функции. Составим таблицу, строки которой соответствуют простым импликантам функции, столбцы – элементам носителя, а в ячейках на пересечении строки и столбца проставлено число , равное 1, если на наборе импликант обращается в единицу, и равное 0 в противном случае. Эта таблица называется импликантной.

		...		…
…
…

Cоставим выражение и совершим переход , рассматривая символы как булевы переменные. После этого в полученном выражении ликвидируем поглощаемые или дублируемые члены, т.е. совершим преобразования вида , . Тогда каждое дизъюнктное слагаемое в упрощенном выражении будет определять тупиковую ДНФ, а именно: каждое слагаемое представляет собой произведение конъюнкций , дизъюнкция которых есть тупиковая ДНФ функции.

Обратите внимание на следующее обстоятельство: тупиковых ДНФ функции может быть несколько.

В качестве примера, с помощью изложенного выше алгоритма найдем тупиковые ДНФ функции . Совокупность простых импликант функции была найдена нами выше. Обозначим , , , . Составим импликантную таблицу:

	000	100	110	111	011
	1	1	0	0	0
	0	1	1	0	0
	0	0	1	1	0
	0	0	0	1	1

.

Получили две тупиковые ДНФ : и .

3-ий этап: построение минимальных ДНФ.

Минимальные ДНФ функции являются тупиковыми ДНФ. Поэтому, после того как все тупиковые ДНФ построены, нужно отобрать те из них, которые имеют наименьшую сложность (таких может быть несколько). Это и будут минимальные ДНФ.

Например, для функции обе тупиковые ДНФ имеют сложность, равную шести, и, следовательно, обе являются минимальными.

Упражнение 22. Построить минимальные ДНФ функции:

а) ; б) ;

в) ; г) .

◄ а) 1 этап. Строим сокращенную ДНФ функции:

.

2-ой и 3-й этапы для данной функции не актуальны. Действительно, функция зависит от переменных существенным образом и, значит, не может быть представлена ДНФ, содержащей менее трех букв. Следовательно, сокращенная ДНФ функции является также тупиковой и минимальной.

0	0	0	0	1
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	0
0	1	1	0	0
0	1	1	1	1
1	0	0	0	1
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	0
1	1	1	0	1
1	1	1	1	1

б) 1-й этап. Строим сокращенную ДНФ функции:

.

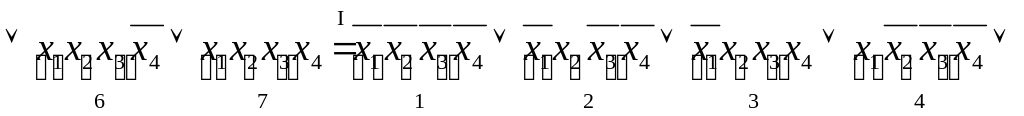
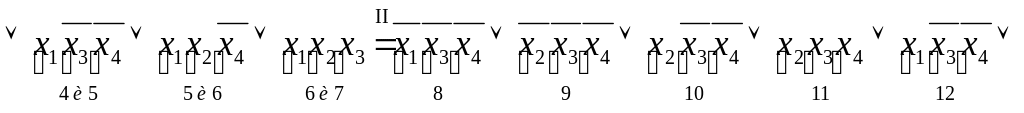
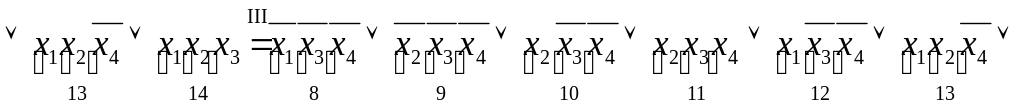
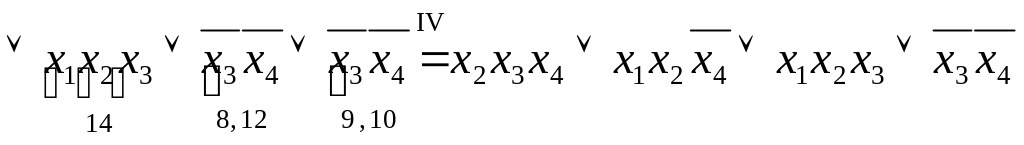Переход I: операция неполного склеивания применена к парам конъюнкций 1 и 2, 1 и 4, 2 и 5, 3 и 7, 4 и 5, 5 и 6, 6 и 7.

Переход II: применена операция поглощения - каждая из конъюнкций 4-го ранга поглощена какой-то из конъюнкций 3-го ранга.

Переход III: операция неполного склеивания применена к парам конъюнкций 8 и 12, 9 и 10.

Переход IV: применена операция поглощения и убраны дублирующие члены.

Итак, мы нашли сокращенную ДНФ функции: .

2-й этап. Введем обозначения для простых импликант функции: , , , . Составим импликантную таблицу:

	0000	0100	0111	1000	1100	1110	1111
	0	0	1	0	0	0	1
	0	0	0	0	0	1	0
	0	0	0	0	0	1	1
	1	1	0	1	1	0	0

Тогда

.

Таким образом, имеем две тупиковых ДНФ, реализующие функцию : и .

3-й этап. Тупиковые ДНФ функции имеют одинаковую сложность (равную восьми), и, следовательно, обе являются минимальными.

в), г) решите самостоятельно. ►