
- •Глава 2. Булевы функции
- •Часть 1
- •§ 2.1. Булевы функции и способы их задания
- •2.1.1. Понятие булевой функции.
- •Примеры булевых функций
- •2.1.2. Реализация булевых функций формулами
- •§ 2.2. Нормальные формы
- •2.2.1. Принцип двойственности
- •2.2.2. Реализация булевых функций в виде сднф и скнф.
- •§ 2.3. Минимизация булевых функций в классе днф
- •§ 2.4. Классы Поста и полнота
- •2.4.1. Понятие о полноте системы булевых функций
- •2.4.2. Реализация булевых функций полиномом Жегалкина
- •2.4.3 Классы Поста
- •2.4.4. Критерий полноты
- •Проверочный тест
- •Ключи теста
- •Глава 2. Часть 2
Ключи теста
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|||||||||
3 |
4 |
1,4 |
1 |
2 |
3 |
4 |
2 |
1,2,3 |
1,3 |
3 |
3 |
1 |
2 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
г |
а |
б |
в |
в |
г |
б |
а |
б |
а |
г |
в |
||||||||||
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
2,4 |
1,3,4 |
2 |
4 |
1,2 |
1,2 |
1,2,3 |
1,4 |
3 |
1,2,3,4,5 |
3 |
1,3,5 |
Глава 2. Часть 2
Вторая часть тематически повторяет первую, но предполагает более глубокое осмысление материала. В тексте приведены все важные утверждения, составляющие теоретическую основу теории булевых функций. Однако доказательств теорем и утверждений в готовом виде в тексте почти нет. Вы можете узнать их, действуя двояко. Первый путь - сразу засесть за учебные пособия (список прилагается) и проработать соответствующие разделы. Второй путь – доказать часть теоретических фактов самостоятельно. Это вполне реально, в особенности, если руководствоваться теми указаниями, которыми мы снабдили каждое утверждение.
Проработав тем или иным способом теоретический кусок, приступайте к выполнению задач и упражнений. Если решения задач и упражнений (или указания к ним) не приведены непосредственно после их формулировки, то их следует искать в конце главы.
ЛИТЕРАТУРА
1. Яблонский С.В. Введение в дискретную математику: учеб. пособие для вузов. / Под. ред. В.А. Садовничего. – 3-е изд., стер. – М.: Высшая школа, 2001. – 384с.
2. Кожухов И.Б., Прокофьев А.А., Соколова Т.В. Курс дискретной математики. – М.: МИЭТ, 2000. – 208 с.
3. Новиков Ф.Н. Дискретная математика для программистов.– СПб.: Питер, 2002.– 304 с.
Пусть
- некоторое подмножество функций из
;
-
множество символов, используемых для
обозначения переменных (алфавит
переменных);
-
множество символов, используемых для
обозначения функций из множества
(алфавит функций). Далее по умолчанию
будем полагать, что
![]() ,
,
![]() .
.
Сопоставим каждой
формуле
![]() над
функцию
над
функцию
![]() по
следующему
индуктивному правилу:
по
следующему
индуктивному правилу:
Базис индукции. Если совпадает с , где
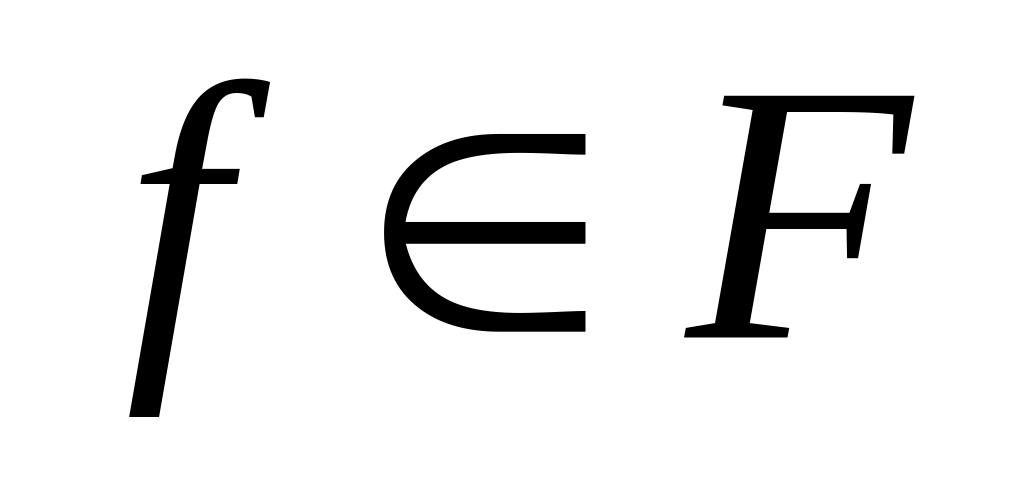 ,
то формуле
сопоставим функцию
.
,
то формуле
сопоставим функцию
.Индуктивный переход. Если формула совпадает с
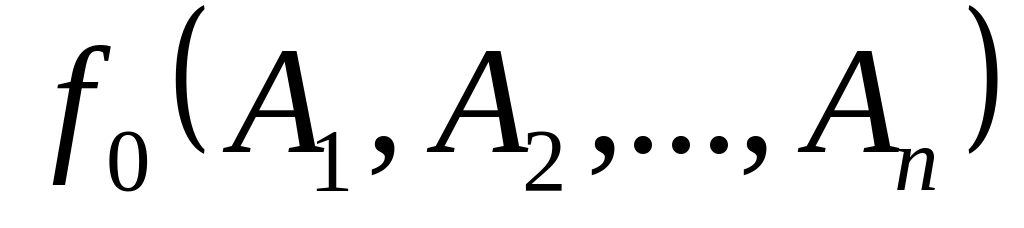 ,
где
,
где
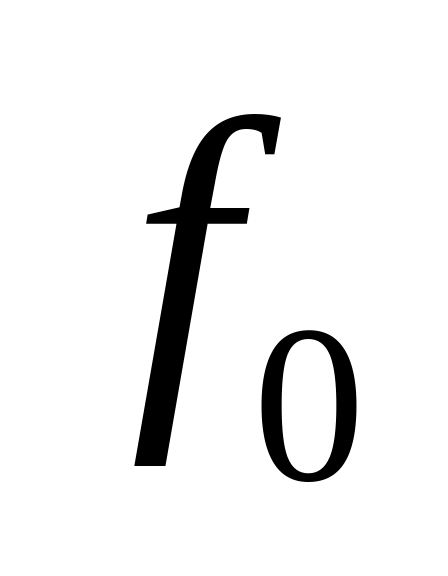 - символ функции из
,
- символ функции из
,
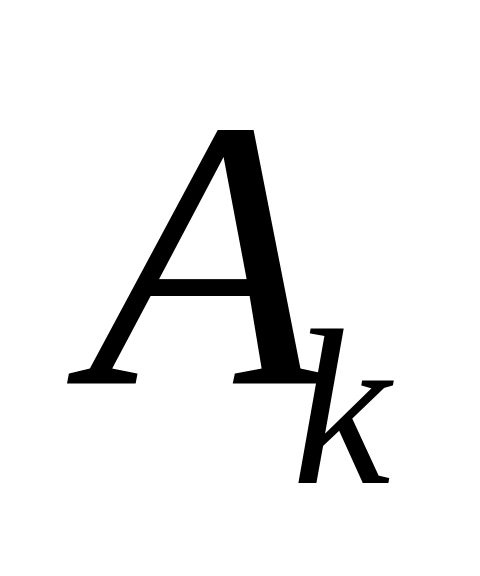
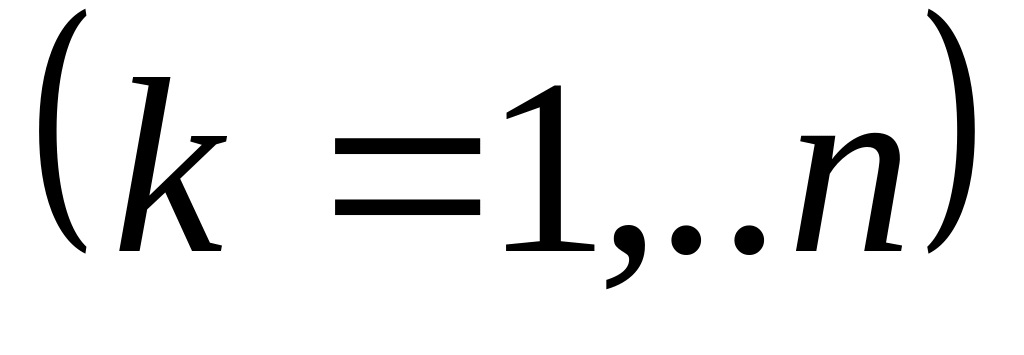 - либо
формула над
,
либо символ переменной
- либо
формула над
,
либо символ переменной
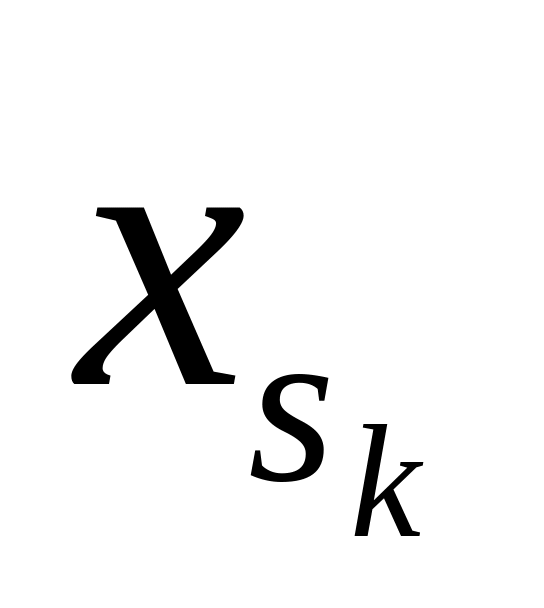 ,
то
тогда, по предположению индукции, в
первом случае
сопоставляется
функция
,
то
тогда, по предположению индукции, в
первом случае
сопоставляется
функция
 из
из
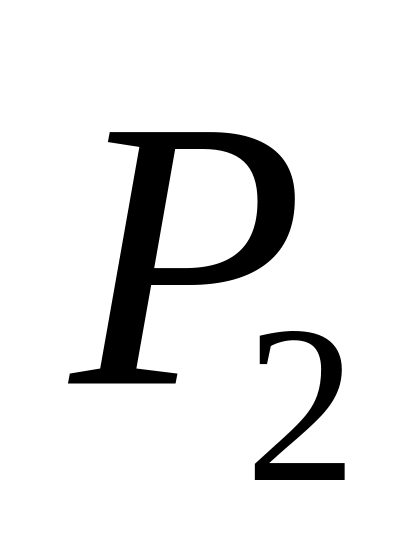 ,
а во втором случае
сопоставляется
тождественная
функция
,
а во втором случае
сопоставляется
тождественная
функция
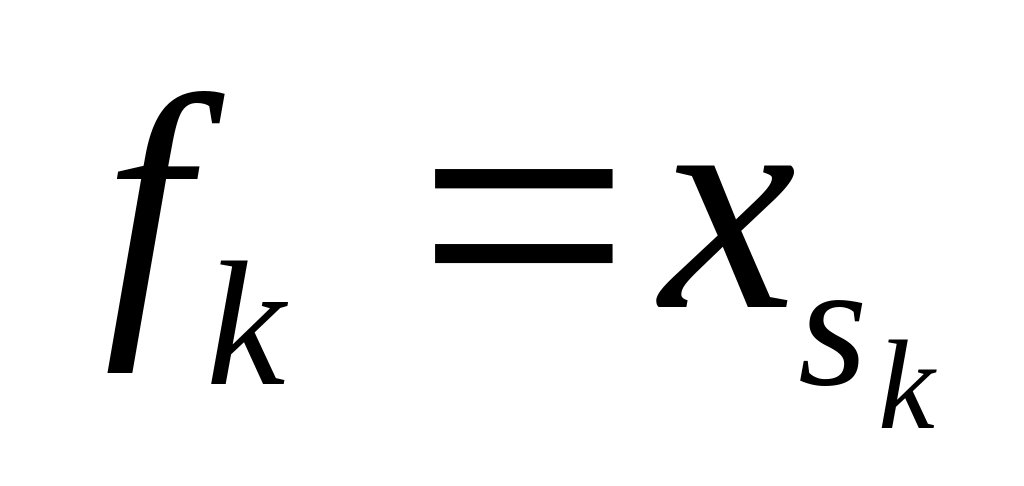 .
Сопоставим формуле
функцию
.
Сопоставим формуле
функцию
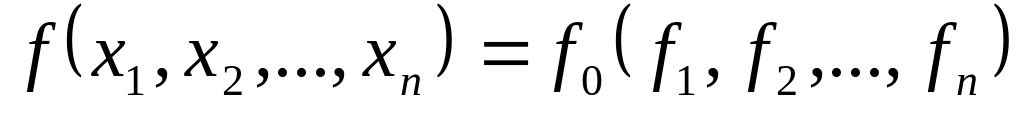 ;
значение функции
на каждом наборе
;
значение функции
на каждом наборе
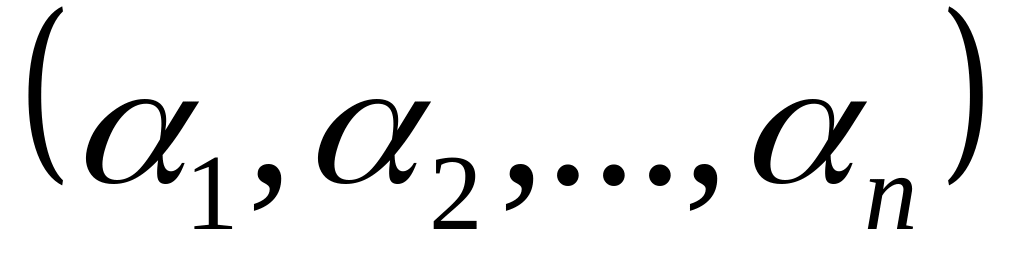 находится как значение функции
на наборе
находится как значение функции
на наборе
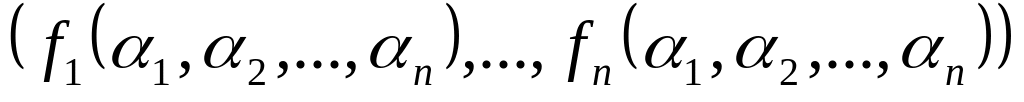 .
.
Упражнение
2.42. Пусть
![]() - подмножество булевых функций, причем
- подмножество булевых функций, причем
![]() ,
,
![]() ,
,
![]() ,
,
![]() - алфавит переменных. Определить,
является ли выражение формулой над
множеством
независимо от вида функций
- алфавит переменных. Определить,
является ли выражение формулой над
множеством
независимо от вида функций
![]() :
:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
е)
![]() ;
ж)
;
ж)
![]() .
.
◄ Выражения а), в), г) являются; б) не является, т.к. тождественный ноль не входит в систему ; е) не является, т. к. функция зависит от трех переменных; ж) не является, т.к. тождественная единица не входит в систему . ►
Утверждение.
Если формула
![]() реализует функцию
реализует функцию
![]() ,
то формула
,
то формула
![]() реализует функцию
реализует функцию
![]() .
.
◄ Указание:
Согласно определению двойственной
функции
![]() .
Следовательно,
.
Следовательно,
![]() .
Эту формулу следует преобразовать,
используя тождества
.
Эту формулу следует преобразовать,
используя тождества
![]() .
►
.
►
Напомним, что
![]()
Упражнение
2.45. а)
Показать,
что
![]() .
.
б)
Показать, что
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() ,
,
![]() .
.
Утверждение
(Теорема
о разложении функций по переменным).
Каждую
булеву
функцию
при любом
![]() можно реализовать формулой:
можно реализовать формулой:
![]() .
(*)
.
(*)
◄ Указание:
Покажите, что на произвольном наборе
значений переменных значение функции,
реализуемой формулой (*), равно
![]() .
Для этого преобразуйте выражение
.
Для этого преобразуйте выражение
![]() ,
,
выделив слагаемое,
соответствующее вектору
![]() .
►
.
►
Упражнение
2.46. а)
Записать
разложение функции
![]() по переменной
.
по переменной
.
б) Записать разложение функции по переменным .
в) Записать разложение функции по всем переменным.
Утверждение (Теорема о реализации функции в виде СДНФ). Если , то она может быть реализована формулой .
Эту формулу называют совершенной дизъюнктивной нормальной формой или, сокращенно, СДНФ.
◄ Указание:
Запишите разложение функции по всем
переменным
![]() и преобразуйте его, разбив на два
слагаемых – дизъюнкции по булевым
векторам, на которых функция равна 1, и
дизъюнкции по булевым векторам, на
которых функция равна 0. ►
и преобразуйте его, разбив на два
слагаемых – дизъюнкции по булевым
векторам, на которых функция равна 1, и
дизъюнкции по булевым векторам, на
которых функция равна 0. ►
Утверждение (Теорема о реализации функции в виде СКНФ). Если , то она может быть реализована формулой .
Эту формулу называют совершенной конъюнктивной нормальной формой или, сокращенно, СКНФ.
◄ Указание.
Воспользуйтесь тем, что
![]() .
В правой части этого равенства запишите
в виде СДНФ,
после чего формулу упростите,
воспользовавшись следствием принципа
двойственности (см. ч.1). ►
.
В правой части этого равенства запишите
в виде СДНФ,
после чего формулу упростите,
воспользовавшись следствием принципа
двойственности (см. ч.1). ►
Упражнение 47. Подсчитать число функций от n переменных, для которых данная элементарная конъюнкция ранга r является импликантой.
Утверждение. Сокращенная ДНФ функции реализует функцию .
◄ Указание. Покажите, что на каждом наборе , на котором функция равна 1, сокращенная ДНФ также обращается в 1 и наоборот. ►
Утверждение. Минимальная ДНФ функции является дизъюнкцией простых импликант этой функции.
◄ Указание. Рассуждайте от противного: пусть в минимальную ДНФ входит импликанта , не являющаяся простой. Рассмотрите ДНФ, которая получается из минимальной ДНФ функции заменой этой импликанты на простую, полученную из опусканием некоторых букв. ►
Утверждение. Минимальная ДНФ функции является тупиковой ДНФ.
◄ Указание. Вновь помогут рассуждения от противного. ►
Утверждение. Сокращенную ДНФ функции можно получить из ее совершенной ДНФ, применяя вначале все возможные операции неполного склеивания, а затем операции поглощения.
◄ Вначале покажем, что из СДНФ операцией полного склеивания можно получить произвольную простую импликанту функции .
Пусть
![]() - произвольная простая импликанта
функции. Из
операцией,
обратной операции полного склеивания,
можно получить
дизъюнкцию элементарных конъюнкций,
входящих в СДНФ функции
.
Действительно, будем последовательно
добавлять переменные, от которых зависит
функция
,
но которые не входят в простую импликанту
.
Так, если в простую импликанту
не входит переменная
- произвольная простая импликанта
функции. Из
операцией,
обратной операции полного склеивания,
можно получить
дизъюнкцию элементарных конъюнкций,
входящих в СДНФ функции
.
Действительно, будем последовательно
добавлять переменные, от которых зависит
функция
,
но которые не входят в простую импликанту
.
Так, если в простую импликанту
не входит переменная
![]() ,
то заменяем
на
,
то заменяем
на
![]() ;
аналогично можно внести недостающие
переменные в элементарные конъюнкции
;
аналогично можно внести недостающие
переменные в элементарные конъюнкции
![]() и
и
![]() .
Продолжая этот процесс, получим
дизъюнкцию всевозможных элементарных
конъюнкций, содержащих
в качестве множителя. Эти элементарные
конъюнкции входят в СДНФ (обоснуйте!)
и их дизъюнкция является частью СДНФ.
.
Продолжая этот процесс, получим
дизъюнкцию всевозможных элементарных
конъюнкций, содержащих
в качестве множителя. Эти элементарные
конъюнкции входят в СДНФ (обоснуйте!)
и их дизъюнкция является частью СДНФ.
Легко видеть, что процесс перехода от простой импликанты к части СДНФ обратим, т.е. с помощью операции полного склеивания можно из этой части совершенной СДНФ получить простую импликанту . Может случиться, что одна и та же элементарная конъюнкция совершенной ДНФ необходима для получения разных простых импликант. Поэтому необходимо применять операцию неполного склеивания, которая сохраняет все элементарные конъюнкции.
Итак, из СДНФ
операцией неполного склеивания получены
все простые импликанты. Теперь надо
удалить из полученной ДНФ все элементарные
конъюнкции, не являющиеся простыми
импликантами функции
.
Всякую элементарную конъюнкцию
,
не являющуюся простой импликантой,
можно представить в виде
![]() ,
где
- простая импликанта. Импликанты
и
входят в ДНФ, полученную из СДНФ операцией
неполного склеивания, поэтому, применяя
к ним операцию поглощения, получим ДНФ,
не содержащую
.
,
где
- простая импликанта. Импликанты
и
входят в ДНФ, полученную из СДНФ операцией
неполного склеивания, поэтому, применяя
к ним операцию поглощения, получим ДНФ,
не содержащую
.
И последнее: если
в полученной после всех вышеописанных
преобразований ДНФ встречаются
одинаковые конъюнкции, необходимо
избавиться от дублирующих членов,
используя равносильность
![]() .►
.►
Определение.
Пусть
- некоторое подмножество
![]() .
Множество всех булевых функций,
реализуемых формулой над
,
называется замыканием
и обозначается
.
Множество всех булевых функций,
реализуемых формулой над
,
называется замыканием
и обозначается
![]() .
.
Например,
если
![]() ,
то
,
то
![]() (с точностью до обозначения переменных
и равных функций).
(с точностью до обозначения переменных
и равных функций).
Операцию получения множества из называют операцией замыкания.
Утверждение. Операция замыкания обладает следующими свойствами:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
2.
![]() .
.
◄ Указание.
Чтобы доказать, например, свойство 4
рассуждаем так: пусть
- произвольная функция, принадлежащая
множеству
![]() ,
надо показать, что эта функция принадлежит
множеству
,
надо показать, что эта функция принадлежит
множеству
![]() .►
.►
Упражнение
2.48. а)
Показать,
что если
![]() ,
то
,
то
![]() .
.
б)
Показать, что
если
![]() ,
то
,
то
![]() .
.
Утверждение. Множество функций, сохраняющих 0, - замкнутый класс.
◄ Указание.
Наша Упражнение показать, что
![]() ,
т.е. что
,
т.е. что
![]() и
и
![]() .
Первое вложение имеет место согласно
первому свойству операции замыкания.
Поскольку класс
содержит тождественную функцию, для
доказательства второго вложения
достаточно показать, что функция
.
Первое вложение имеет место согласно
первому свойству операции замыкания.
Поскольку класс
содержит тождественную функцию, для
доказательства второго вложения
достаточно показать, что функция
![]() ,
если
.
Вычислите для этого
,
если
.
Вычислите для этого
![]() .
►
.
►
Утверждение. Множество функций, сохраняющих 1, - замкнутый класс.
◄ Указание. Доказывается по аналогии с предыдущим утверждением. ►
Утверждение. Множество самодвойственных функций - замкнутый класс.
◄ Указание.
Наша Упражнение показать, что
![]() ,
т.е., что
,
т.е., что
![]() и
и
![]() .
Согласно первому свойству замыкания
.
Докажем, что и
.
Поскольку класс
содержит тождественную функцию, для
доказательства второго вложения
достаточно показать, что если
.
Согласно первому свойству замыкания
.
Докажем, что и
.
Поскольку класс
содержит тождественную функцию, для
доказательства второго вложения
достаточно показать, что если
![]() ,
то
,
то
![]() (т.е.
(т.е.
![]() ).
Для этого используем принцип
двойственности. ►
).
Для этого используем принцип
двойственности. ►
Утверждение. Множество монотонных функций - замкнутый класс.
◄ Указание.
Наша Упражнение показать, что
![]() т.е. что
т.е. что
![]() и
и
![]() .
Поскольку класс
содержит тождественную функцию, для
доказательства второго вложения
достаточно показать, что функция
.
Поскольку класс
содержит тождественную функцию, для
доказательства второго вложения
достаточно показать, что функция
![]() ,
если
,
если
![]() .
Чтобы убедиться, что
.
Чтобы убедиться, что
![]() ,
советуем вначале использовать
монотонность функций
,
советуем вначале использовать
монотонность функций
![]() ,
а затем монотонность функции
.
►
,
а затем монотонность функции
.
►
Утверждение. Множество линейных функций - замкнутый класс.
◄ Указание.
Наша Упражнение показать, что
Указание.
Наша Упражнение показать, что
![]() т.е. что
т.е. что
![]() и
и
![]() .
Поскольку класс
содержит тождественную функцию, то для
доказательства второго вложения, нам
достаточно показать, что функция
.
Поскольку класс
содержит тождественную функцию, то для
доказательства второго вложения, нам
достаточно показать, что функция
![]() ,
если
,
если
![]() .
Советуем преобразовать формулу
.
Советуем преобразовать формулу
![]() ,
предварительно записав каждую из
функций
,
в виде полинома Жегалкина. ►
,
предварительно записав каждую из
функций
,
в виде полинома Жегалкина. ►
Утверждение
(лемма
о функции, не сохраняющей 0).
Пусть
![]() .
Тогда формулой над множеством
.
Тогда формулой над множеством
![]() можно реализовать либо константу 1,
либо отрицание.
можно реализовать либо константу 1,
либо отрицание.
◄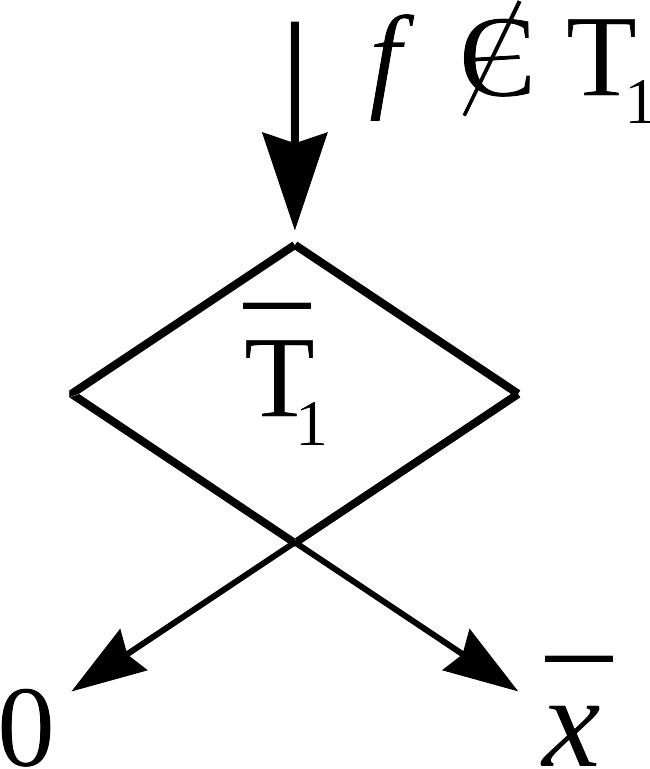 Указание.
Рассмотрите функцию, реализуемую
формулой
Указание.
Рассмотрите функцию, реализуемую
формулой
![]() .
►
.
►
Утверждение
(лемма
о функции, не сохраняющей 1).
Пусть
![]() .
Тогда формулой над множеством
можно реализовать либо константу 0,
либо отрицание.
.
Тогда формулой над множеством
можно реализовать либо константу 0,
либо отрицание.
◄ Указание. Рассмотрите функцию, реализуемую формулой . ►
Упражнение
2.49.
Реализовать формулой над множеством
![]() либо 0, либо 1, либо отрицание.
либо 0, либо 1, либо отрицание.
У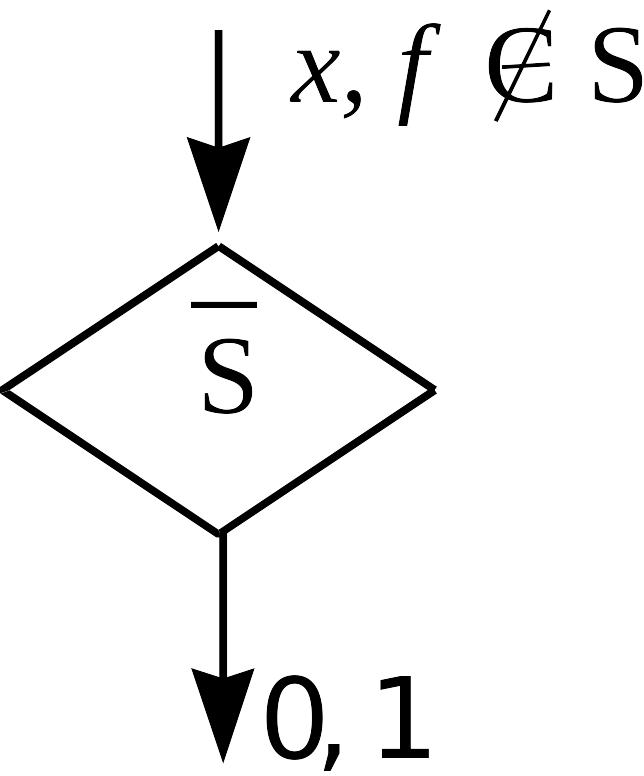 тверждение
(лемма о несамодвойственной функции).
Пусть
тверждение
(лемма о несамодвойственной функции).
Пусть
![]() .
Тогда формулой над множеством
.
Тогда формулой над множеством
![]() можно реализовать константы 0 и 1.
можно реализовать константы 0 и 1.
◄ Указание.
Если
,
то существует такой набор
значений переменных, что
![]() .
Рассмотрите функцию, реализуемую
формулой
.
Рассмотрите функцию, реализуемую
формулой
![]() .
►
.
►
Упражнение
2.50.
Реализовать формулой над множеством
![]() константы 0 и 1.
константы 0 и 1.
Утверждение
(лемма о немонотонной функции).
Пусть
![]() .
Тогда формулой над множеством
.
Тогда формулой над множеством
![]() можно реализовать отрицание.
можно реализовать отрицание.
◄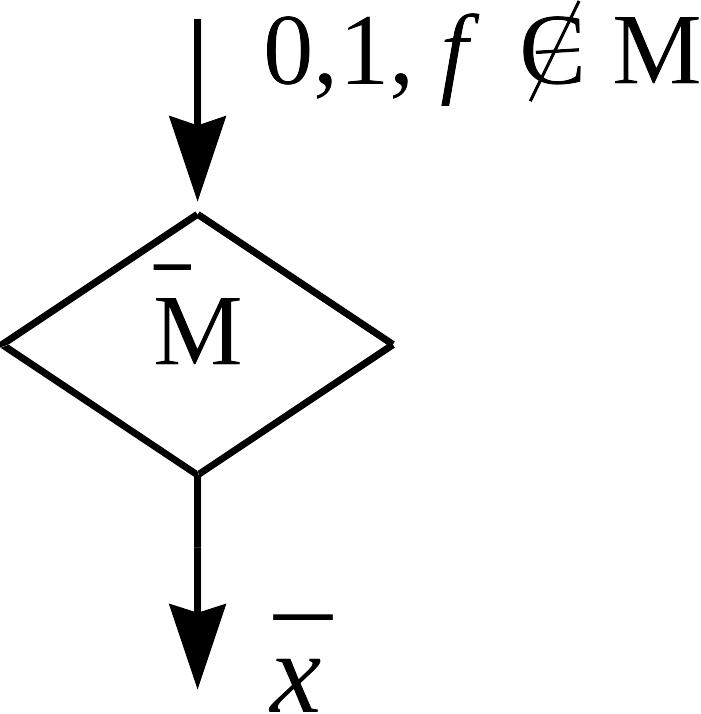 Указание.
Если
,
то существуют такие наборы
и
Указание.
Если
,
то существуют такие наборы
и
![]() значений переменных, что
значений переменных, что
![]() ,
а
,
а
![]() .
Поскольку
.
Поскольку
![]() ,
то можно выделить подпоследовательность
индексов
,
то можно выделить подпоследовательность
индексов
![]() такую, что:
такую, что:
![]() и для всякого
и для всякого
![]()
![]() .
.
Рассмотрите
функцию
![]() ,
реализуемую формулой, получающейся в
результате подстановки в формулу
на места
,
реализуемую формулой, получающейся в
результате подстановки в формулу
на места
![]() чисел
чисел
![]() ,
а на остальные места -
,
т.е.
,
а на остальные места -
,
т.е.
![]() .►
.►
Упражнение
2.51.
Реализовать формулой над множеством
![]() отрицание.
отрицание.
Утверждение
(лемма о нелинейной функции).
Пусть
![]() .
Тогда формулой над множеством
.
Тогда формулой над множеством
![]() можно реализовать конъюнкцию.
можно реализовать конъюнкцию.
◄ Указание.
Пусть
,
тогда в каноническом полиноме Жегалкина
данной функции найдется член с отличным
от нуля коэффициентом, содержащий
произведения переменных. Не нарушая
общности рассуждений, можно считать,
что этот член содержит
![]() .
Следовательно, полином Жегалкина
функции
можно преобразовать к виду
.
Следовательно, полином Жегалкина
функции
можно преобразовать к виду
![]()
![]() ,
,
где функция
такова, что найдется набор
![]() значений переменных такой, что
значений переменных такой, что
![]() .
.
П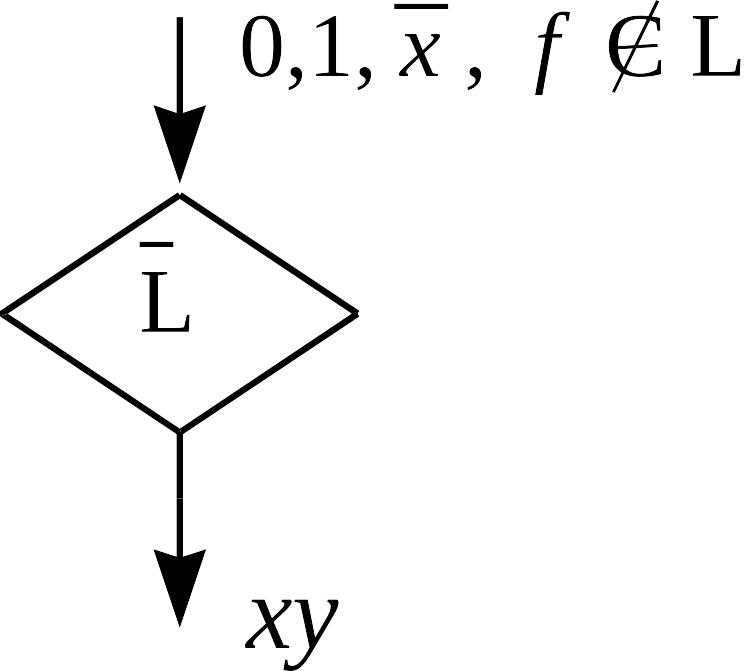 усть
усть
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тогда для реализации конъюнкции годится
формула
.
Тогда для реализации конъюнкции годится
формула
![]() .
Ваша Упражнение - убедиться в этом (для
этого достаточно упростить формулу,
используя равносильные преобразования).
►
.
Ваша Упражнение - убедиться в этом (для
этого достаточно упростить формулу,
используя равносильные преобразования).
►
Упражнение
2.52.
Реализовать формулой над множеством
![]() отрицание.
отрицание.
Утверждение. Классы Поста неполны.
◄ Будем рассуждать от противного, т.е. предположим, что какой-то из классов Поста полон. Тогда любая булева функция принадлежит его замыканию, а, следовательно, в силу его замкнутости, и ему самому. Но это не так. Например, штрих Шеффера не принадлежит ни одному из классов Поста. ►
Утверждение. Классы Поста попарно различны.
◄ Указание. Чтобы убедиться в попарном различии классов Поста, достаточно для каждой пары классов указать функцию, принадлежащую одному классу из пары и не принадлежащую другому. ►
Теорема (Поста). Для того чтобы система функций была полна, необходимо и достаточно, чтобы множество не являлось подмножеством ни одного из классов Поста.
◄ Необходимость.
Пусть система
полна. Докажем, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Рассуждаем от противного: предположим,
что
- подмножество одного из классов Поста.
Обозначим этот класс
.
Рассуждаем от противного: предположим,
что
- подмножество одного из классов Поста.
Обозначим этот класс
![]() .
Имеем:
.
Имеем:
![]() .
Значит
.
Значит
![]() ,
что не так.
,
что не так.
Достаточность.
Пусть
,
,
,
,
.Тогда
найдутся функции
![]() из
такие,
что
из
такие,
что
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Покажем, что отрицание и конъюнкцию
можно реализовать формулами над
множеством
.
Покажем, что отрицание и конъюнкцию
можно реализовать формулами над
множеством
![]() .
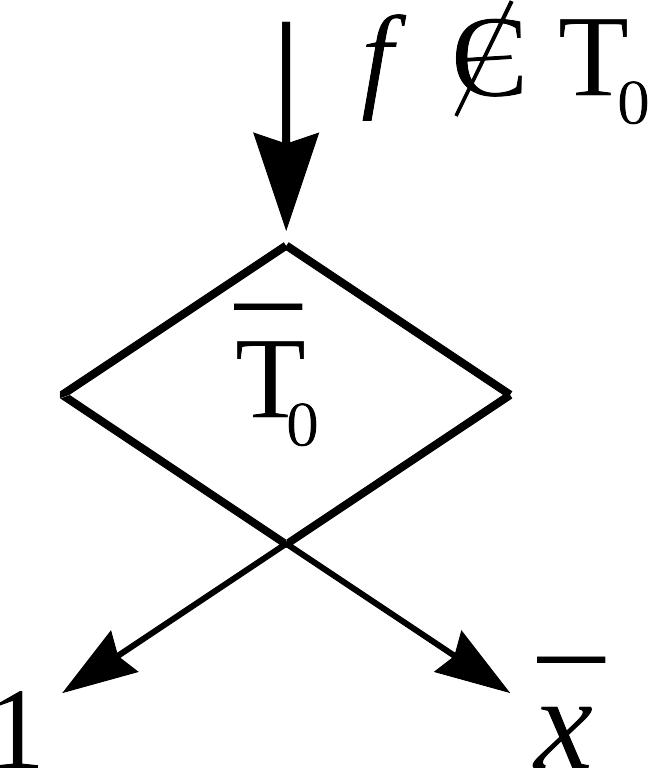
Процедуру построения соответствующих
формул можно представить схемой:
.
Процедуру построения соответствующих
формул можно представить схемой:
Т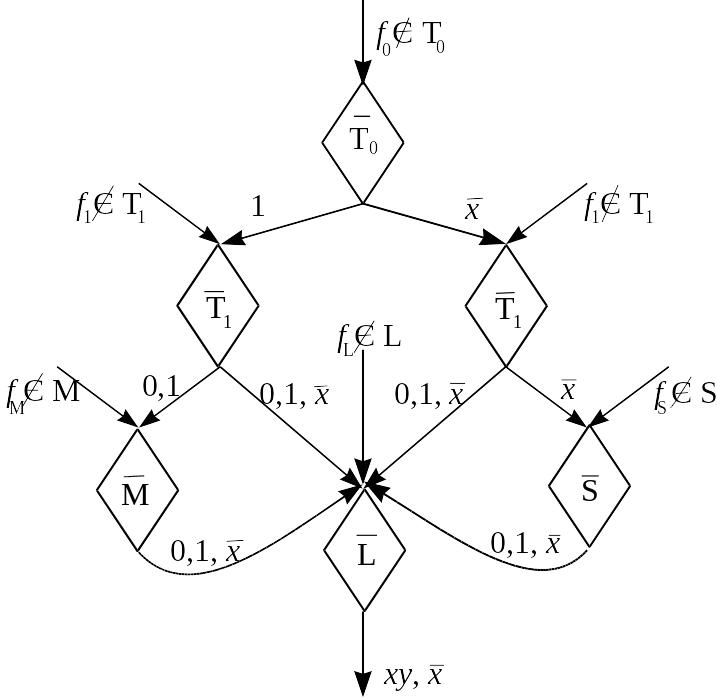 аким
образом, конъюнкцию и отрицание можно
реализовать формулой над
.
Имеем:
аким
образом, конъюнкцию и отрицание можно
реализовать формулой над
.
Имеем:
![]() - полная система, причем каждая ее
функция может быть выражена формулой
над
.
Следовательно, условия теоремы о
полноте двух систем выполнены и, значит,
- полная система. ►
- полная система, причем каждая ее
функция может быть выражена формулой
над
.
Следовательно, условия теоремы о
полноте двух систем выполнены и, значит,
- полная система. ►
Следствие. Из любой полной системы можно выделить полную подсистему, содержащую не более пяти функций.
◄ Так как
![]() полна, то она не принадлежит ни одному
из классов Поста. Значит, найдутся
функции
из
такие, что
,
,
,
,
.
Эти функции и образуют полную подсистему.
Поскольку в этом списке некоторые
функции могли встретиться не по одному
разу, то пять – это максимальное их
число. ►
полна, то она не принадлежит ни одному
из классов Поста. Значит, найдутся
функции
из
такие, что
,
,
,
,
.
Эти функции и образуют полную подсистему.
Поскольку в этом списке некоторые
функции могли встретиться не по одному
разу, то пять – это максимальное их
число. ►
Утверждение. Всякий замкнутый класс функций, не совпадающий с , содержится, по крайней мере, в одном из классов Постов.
Определение. Класс называется предполным классом, если:
неполон;
добавление к любой функции, ему не принадлежащей, приводит к образованию полного множества.
Утверждение. Предполными являются классы Поста и только они.
Указание. Предположите противное и воспользуйтесь критерием полноты.►
Управнение 2.53. Указать существенные и фиктивные переменные функции
![]() (
(![]() ).
).
Упражнение 2.52.
Показать,
что для любых противоположных наборов
и
![]() выполняется
равенство
выполняется
равенство
![]() .
.
Упражнение 2.55. Сколько имеется самодвойственных функций от переменных?
Упражнение 2.56.
б)
Сколько функций содержит множество
![]() ?
?
б)
Сколько
функций содержит множество
![]() ?
?
Упражнение 2.57. Выяснить, сколько линейных функций от переменных сохраняют константу 0 и не сохраняют константу 1.
Упражнение 2.58. Найти число линейных самодвойственных функций.
Упражнение 2.59.
Докажите, что
![]() .
.
Упражнение 2.60.
Пусть
![]() - произвольная булева функция,
- произвольная булева функция,
![]() получена из
путем отождествления всех переменных:
получена из
путем отождествления всех переменных:
![]() .
Определить
,
если а)
.
Определить
,
если а)
![]() ;
б)
;
б)
![]() .
.
Упражнение 2.61.
Доказать, что функцию
нельзя реализовать формулой над
множеством связок
![]() ,
если:
,
если:
а)
![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() ;
;
в)
![]() ,
,
![]() ;
г)
;
г)
![]() ,
,
![]() .
.
Упражнение 2.62.
Показать, что если
![]() ,
то
либо немонотонная, либо несамодвойственная.
,
то
либо немонотонная, либо несамодвойственная.
Упражнение 2.63. Доказать, что из любой полной системы можно выделить полную подсистему, содержащую не более четырех функций.
Упражнение 2.62. Доказать, что функция, двойственная монотонной функции, монотонна.
Упражнение 2.65.
Доказать, что для монотонных функций
справедливо разложение
![]() .
.
Упражнение 2.66. Доказать, что функция, двойственная линейной функции, линейна.
Упражнение 2.67.
Показать, что
![]() является существенной переменной тогда
и только тогда, когда эта переменная
явно входит в сокращенную ДНФ функции.
является существенной переменной тогда
и только тогда, когда эта переменная
явно входит в сокращенную ДНФ функции.
Упражнение 2.68. Показать, что является существенной переменной тогда и только тогда, когда явно входит в полином Жегалкина функции.
Упражнение 2.69. Найти число линейных функций от n переменных, существенно зависящих ровно от k переменных.
Решения и ответы к упражнениям части 2
2.46.
а)
![]() .
.
б)
![]() .
.
в) .
2.47.
Рассмотрим
произвольную функцию
,
для которой некоторая заданная конъюнкция
ранга r
является импликантой. Эта функция
должна обращаться в 1 на булевых векторах
с r
фиксированными координатами. Таких
векторов
![]() .
На остальных наборах общим числом
.
На остальных наборах общим числом
![]() она может принимать произвольные
значения (0 или 1). Следовательно, искомое
число функций равно
она может принимать произвольные
значения (0 или 1). Следовательно, искомое
число функций равно
![]() .
.
2.48. а)![]()
![]()
![]() .
.
б)
![]()
![]()
![]() .
.
2.49.
Так как
и
,
то для решения задачи нам годится
формула
![]() .
Имеем
.
Имеем
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]() .
.
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
2.52.
Запишем для функции
![]() полином Жегалкина:
полином Жегалкина:
![]() .
Так как функция
нелинейна, то для построения формулы
можно использовать алгоритм, использованный
при доказательстве леммы о нелинейной
функции. Запишем полином Жегалкина
функции
.
Так как функция
нелинейна, то для построения формулы
можно использовать алгоритм, использованный
при доказательстве леммы о нелинейной
функции. Запишем полином Жегалкина
функции
![]() в виде:
в виде:
![]() .
.
Поскольку
![]() при
при
![]() ,
то, следуя
лемме, рассмотрим функцию
,
то, следуя
лемме, рассмотрим функцию
![]()
![]() .
.
И, наконец, перейдем к функции
![]()
![]() .
.
2.53. Рассмотрим сначала переменную :
![]()
![]() .
.
![]()
![]() .
.
Возьмем набор
![]() ,
в котором сумма
,
в котором сумма
![]() (например,
(например,
![]() ,
,
![]() ).
Тогда
).
Тогда
![]() ,
а
,
а
![]() .
Таким образом,
.
Таким образом,
![]() ,
следовательно,
- существенная переменная.
,
следовательно,
- существенная переменная.
Об остальных переменных рассуждаем аналогично. Вывод: все переменные функции являются существенными.
2.52.
Напомним, что наборы
и
.
называются противоположными, если
выполнено равенство
![]() .
Поэтому координаты
таких наборов связаны соотношениями
.
Поэтому координаты
таких наборов связаны соотношениями
![]() .
Пусть
.
Пусть
![]() ,
тогда
,
тогда
![]() и
и
![]()
![]() .
.
2.55.
Пусть
![]() .
Тогда для любого набора значений
переменных
.
Тогда для любого набора значений
переменных
![]() выполняется равенство
выполняется равенство
![]() .
Это означает, что на наборах
и
.
Это означает, что на наборах
и
![]() значения функции противоположены.
Значения
значения функции противоположены.
Значения
![]() и
и
![]() расположены в векторе значений функции
на равных расстояниях от правого и
левого конца (напомним, что ранее было
доказано сумма номеров векторов
и
равна
расположены в векторе значений функции
на равных расстояниях от правого и
левого конца (напомним, что ранее было
доказано сумма номеров векторов
и
равна
![]() ).
Значит, для задания функции
достаточно задать первую половину
вектора значений.
Следовательно,
самодвойственных функций от
переменных столько же, сколько булевых
векторов длины
).
Значит, для задания функции
достаточно задать первую половину
вектора значений.
Следовательно,
самодвойственных функций от
переменных столько же, сколько булевых
векторов длины
![]() ,
т.е.
,
т.е.
![]() .
.
2.56.
а) Пусть
![]() .
Тогда
,
как всякая самодвойственная функция,
задается первой половиной вектора
значений. Поскольку
сохраняет константу 1, то первая
координата ее вектора значений равна
0. Значит, чтобы задать функцию
нужно задать
.
Тогда
,
как всякая самодвойственная функция,
задается первой половиной вектора
значений. Поскольку
сохраняет константу 1, то первая
координата ее вектора значений равна
0. Значит, чтобы задать функцию
нужно задать
![]() координату булева вектора. Следовательно,
координату булева вектора. Следовательно,
![]() .
.
б)
![]() .
.
2.57.
Если
![]() линейна, то ее полином Жегалкина можно
записать в виде
линейна, то ее полином Жегалкина можно
записать в виде
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Из условия
.
Из условия
![]() получаем:
получаем:
![]() .
Последнее равенство имеет место, если
четное (или нулевое) число слагаемых
(коэффициентов
.
Последнее равенство имеет место, если
четное (или нулевое) число слагаемых
(коэффициентов
![]() )
равно единице. Таким образом, нас
интересует число булевых векторов
)
равно единице. Таким образом, нас
интересует число булевых векторов
![]() четного или нулевого веса. Каждый такой
вектор характеризуется набором номеров
единичных координат. Таких наборов
столько, сколько подмножеств множества
из n
элементов четной или нулевой мощности,
т.е.
четного или нулевого веса. Каждый такой
вектор характеризуется набором номеров
единичных координат. Таких наборов
столько, сколько подмножеств множества
из n
элементов четной или нулевой мощности,
т.е.
![]() .
.
2.58.
Если
линейна, то ее полином Жегалкина можно
записать в виде
.
Пусть
.
Тогда
![]() и, значит,
и, значит,
![]() ,
,
![]() ,
,
![]() .
.
Из последнего
равенства
![]() .
Таким образом, нас интересует число
булевых векторов
нечетного веса. Таких векторов
.
Коэффициент
.
Таким образом, нас интересует число
булевых векторов
нечетного веса. Таких векторов
.
Коэффициент
![]() можно выбрать произвольно. Таким
образом, число линейных самодвойственных
функций равно
.
можно выбрать произвольно. Таким
образом, число линейных самодвойственных
функций равно
.
2.59.
![]() ,
следовательно,
,
следовательно,
![]() .
Осталось доказать, что
.
Осталось доказать, что
![]() .
Действительно, если
.
Действительно, если
![]() ,
то свободный член в полиноме Жегалкина
этой функции равен 0, значит,
можно выразить формулой через
,
то свободный член в полиноме Жегалкина
этой функции равен 0, значит,
можно выразить формулой через
![]() .
.
2.60.
а) Если
![]() ,
то
,
то
![]() и
и
![]() .
Следовательно,
.
Следовательно,
![]() и
и
![]() .
А это означает, что
.
А это означает, что
![]() .
.
б) Если
![]() ,
то
,
то
![]() .
Возможны два случая: 1)
.
Возможны два случая: 1)
![]() ,
,
тогда
,
,
тогда
![]() и
и
![]() ,
следовательно,
,
следовательно,
![]() ;
;
2)
![]() ,
,
![]() ,
тогда
,
тогда
![]() и
и
![]() ,
следовательно,
,
следовательно,
![]() .
.
2.61.
а) Конъюнкция
принадлежит к классу
![]() .
Класс
является замкнутым множеством,
следовательно, любая функция, реализованная
формулой над его функциями, сохраняет
константу 0. Тот факт, что функция
этим свойством не обладает, означает,
что ее нельзя реализовать формулой над
множеством связок
.
.
Класс
является замкнутым множеством,
следовательно, любая функция, реализованная
формулой над его функциями, сохраняет
константу 0. Тот факт, что функция
этим свойством не обладает, означает,
что ее нельзя реализовать формулой над
множеством связок
.
б)
![]() ,
а
;
в)
,
а
;
в)
![]()
![]() ;
г)
;
г)
![]() .
.
2.62.
По условию
![]() .
Возможны два случая:
.
Возможны два случая:
![]() или
или
![]() .
В первом случае функция
.
В первом случае функция
![]() немонотонная, во втором – несамодвойственная.
немонотонная, во втором – несамодвойственная.
2.63.
В силу полноты
системы
найдутся функции
из
такие, что
,
,
,
,
.
Ранее было показано, что функция
либо немонотонная, либо несамодвойственная.
Следовательно, одна из двух подсистем
![]() ,
,
![]() обязательно полна.
обязательно полна.
2.62. Пусть
![]() и
и
![]() - два произвольных набора, связанных
соотношением
- два произвольных набора, связанных
соотношением
![]() .
Тогда
.
Тогда
![]() .
Так как функция
монотонная, то
.
Так как функция
монотонная, то
![]() .
Значит,
.
Значит,
![]() и, следовательно,
и, следовательно,
![]() ,
что и доказывает монотонность двойственной
функции.
,
что и доказывает монотонность двойственной
функции.
2.65.
Надо показать, что на любом наборе
значений переменных выполняются
равенство
![]() (*).
(*).
Рассмотрим два случая.
1) Пусть в наборе
переменная
![]() .
Тогда левая часть (*) преобразуется к
виду
.
Тогда левая часть (*) преобразуется к
виду
![]() ,
т.е. на наборах
,
т.е. на наборах
![]() равенство (*) выполняется.
равенство (*) выполняется.
2) Пусть
в наборе
переменная
![]() .
Тогда правая часть (*) преобразуется к
виду
.
Тогда правая часть (*) преобразуется к
виду
![]() .
Поскольку
.
Поскольку
![]() ,
а
- монотонная, то
,
а
- монотонная, то
![]() ,
и, значит,
,
и, значит,
![]() .
Таким образом, на наборах
.
Таким образом, на наборах
![]() равенство (*) также выполняется.
равенство (*) также выполняется.
2.66.
Если
линейна, то ее полином Жегалкина можно
записать в виде
.
Тогда согласно определению двойственной
функции
![]() .
Преобразуем это выражение:
.
Преобразуем это выражение:
![]()
![]() .
.
Таким образом,
степень полинома Жегалкина функции
![]() не выше первой, что и доказывает
линейность этой функции.
не выше первой, что и доказывает
линейность этой функции.
2.67. Пусть для определенности речь идет о переменной (это не нарушит общности рассуждений).
Необходимость.
Рассуждаем
от противного: предположим, что
,
будучи существенной переменной, не
входит в сокращенную ДНФ (обозначим ее
)
функции
.
Поскольку
реализует
,
то верны равенства:
![]() .
Значит,
- фиктивная. Пришли к противоречию с
условием.
.
Значит,
- фиктивная. Пришли к противоречию с
условием.
Достаточность.
Будем
рассуждать от противного: предположим,
что
входит в сокращенную ДНФ, но при этом
является фиктивной. Раз
входит в сокращенную ДНФ, а сокращенная
ДНФ – дизъюнкция всех простых импликант
функции
,
то найдется простая импликанта
,
содержащая либо
,
либо
![]() (пусть для определенности это будет
).
Пусть
(пусть для определенности это будет
).
Пусть
![]() - конъюнкция, получающаяся из
путем удаления
(
- конъюнкция, получающаяся из
путем удаления
(![]() ).
уже импликантой не является, следовательно,
найдется такой набор
значений переменных, что
).
уже импликантой не является, следовательно,
найдется такой набор
значений переменных, что
![]() ,
а
,
а
![]() .
Поскольку
.
Поскольку
![]() ,
а, значит, и
,
а, значит, и
![]() ,
то
,
если
,
то
,
если
![]() .
Одновременное выполнение равенств
и
.
Одновременное выполнение равенств
и
![]() противоречит предположению о фиктивности
.
противоречит предположению о фиктивности
.
2.68. Пусть для определенности речь идет о переменной (это не нарушит общности рассуждений).
Необходимость покажите самостоятельно.
Достаточность.
Будем
рассуждать от противного: предположим,
что
входит явно в полином Жегалкина
![]() функции
,
но при этом является фиктивной. Если
входит явно в полином
,
то его можно записать в виде
функции
,
но при этом является фиктивной. Если
входит явно в полином
,
то его можно записать в виде
![]() ,
где
,
где
![]() и
и
![]() полиномы и
тождественно отличен от нуля. Пусть
полиномы и
тождественно отличен от нуля. Пусть
![]() набор такой, что
набор такой, что
![]() .
.
![]() .
Тогда
.
Тогда
![]() ,
а
,
а
![]() ,
следовательно,
,
следовательно,
![]() ,
и, значит,
,
и, значит,
![]() ,
т.е. переменная
- существенная. Пришли к противоречию.
,
т.е. переменная
- существенная. Пришли к противоречию.
2.69.
Если
линейна, то ее полином Жегалкина можно
записать в виде
.
Мы знаем, что
является существенной переменной тогда
и только тогда, когда
явно входит в полином Жегалкина.
Следовательно, интересующие нас полиномы
Жегалкина определяются набором
коэффициентов
![]() ,
в котором
равно либо 0, либо 1, а среди
ровно k
коэффициентов
равны 1. Выбрать из n
коэффициентов
k
можно
способами. Следовательно, можно составить
,
в котором
равно либо 0, либо 1, а среди
ровно k
коэффициентов
равны 1. Выбрать из n
коэффициентов
k
можно
способами. Следовательно, можно составить
![]() требуемых наборов значений коэффициентов.
требуемых наборов значений коэффициентов.
