2.4. Решение систем нелинейных уравнений.

При решении системы уравнений очень сложно отделить корни. Для получения всех возможных решений чаще всего на практике перебирают различные начальные условия поиска.

Метод итераций аналогичен соответствующему методу при решении одного уравнения. Все уравнения системы приводятся к виду:

x₁=f₁(x₁, x₂, …, x_n)

x₂=f₂(x₁, x₂, …, x_n)

…

x_n=f_n(x₁, x₂, …, x_n)

Произвольные начальные значения подставляются в уравнения системы. Из каждого уравнения системы находятся новые значения и т.д. При выполнении условий или

последовательность сходится к решению

ЗАДАЧА 2.5. Решить систему уравнений

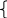sin(x₁-0,6)-x₂=1,6

3x₁-cos x₂=0,9

E – погрешность вычислений

РЕШЕНИЕ

СВЯЗЬ. Преобразуем систему к виду:

x₂ =sin(x₁-0,6) -1,6= f₂(x₁, x₂)

x₁=(cos x₂)/3+0,3= f₁(x₁, x₂)

Проверим условие сходимости:

и

Выберем по графику начальные значения х₁⁰=0,15 и х₂⁰=-2

x₂ⁱ⁺¹ =sin(x₁ⁱ-0,6) -1,6

x₁ⁱ⁺¹=(cos x₂ⁱ)/3+0,3

x₁= x₁ⁱ⁺¹, x₂= x₂ⁱ⁺¹ при /x₁ⁱ⁺¹ –x₁ⁱ/<E , /x₂ⁱ⁺¹ –x₂ⁱ/<E

3. Решение систем линейных уравнений.

3.1. Классификация методов

Методы решения

Точные

Приближенные

Метод Гаусса

Метод Крамера

Метод простой итерации

Метод Зейделя

3.2. Точные методы.

Точные методы позволяют для любых систем линейных уравнений Ах=В в принципе найти точные значения переменных. Но при использовании этих методов может появиться накапливающаяся вычислительная ошибка (не алгоритмическая!). В результате значения переменных могут быть получены с некоторой погрешностью. При высоких порядках системы погрешность может оказаться значительной. Ошибка в вычислениях неизбежно приводит к ошибке в результате. Для контроля вычислительной ошибки применяют специальные приемы.

Метод Гаусса заключается в последовательном исключении неизвестных. Метод сводится к двум этапам. 1 этап – приведение исходной системы уравнений с помощью эквивалентных преобразований к системе с верхней треугольной матрицей (к треугольному виду). 2 этап – последовательное нахождение всех переменных системы, начиная с последней..

Затем можно найти невязки δ=В-Ах и вычислить поправки ε к полученным значениям переменных, решив систему уравнений Аε= δ.

Метод Крамера заключается в нахождении значений переменных с помощью определителей

ЗАДАЧА 3.1.

Решить систему уравнений Ах=В методами Гаусса и Крамера

РЕШЕНИЕ.

1) Приведем систему к треугольному виду.

Найдем приближенные корни: x₃=3; x₂=2,02; x₁=0,97

Вычислим невязки: δ₁=3∙0,97+2∙2,02+2∙3 – 13 = 0,05; δ₂=0; δ₃=0,02

Решив систему Аε= δ, получим: ε₁=0,03; ε₂=-0,02; ε₃=0,00014

Уточненные решения: x₃=3; x₂=2,02-0,02=2; x₁=0,97+0,03=1

2) Вычислим определители системы и найдем корни по методу Крамера.

Задание 3.1.

Решить систему уравнений точными методами.

3.3. Схема единственного деления.

Для удобства вычисления по методу Гаусса производятся по схеме единственного деления. Процесс преобразования матрицы к треугольной называется прямым ходом, а вычисление значений неизвестных – обратным ходом.

Количество разделов прямого хода равно числу неизвестных системы уравнений. В раздел I схемы записываются коэффициенты при неизвестных; свободные члены, контрольные суммы и строчные суммы, равные сумме всех элементов строки. Последняя строка (b_1j) получается делением первой строки раздела (a_1j) на ведущий элемент (a₁₁ –первый элемент раздела) :

Элементы раздела II вычисляются по формуле: a_ij^(II)= a_ij^(I)– a_i1^(I) · b_1j . Последняя строка раздела вычисляется делением первой строки раздела на ведущий элемент.

Аналогично вычисляются элементы следующих разделов.

Обратный ход начинается с вычисления последнего неизвестного системы уравнений и заканчивается вычислением первого неизвестного, используя лишь последние строки каждого раздела.

Строчные суммы всегда равны суммам элементов своей строки (без контрольной суммы), Над контрольными суммами в каждой строке проделываются те же операции, что и над остальными элементами этой строки. При отсутствии ошибок в вычислениях контрольные суммы приближенно равны строчным.

При необходимости уточнения корней х⁽⁰⁾ системы уравнений необходимо:

- вычислить невязки δ =В – Ах⁽⁰⁾;

- выписать невязки в столбец ε схемы;

- считая столбец ε столбцом свободных членов, вычислить ε₁, ε₂, …ε_n как значения неизвестных

- найти уточненные значения неизвестных: х = х⁽⁰⁾ + ε

ЗАДАЧА 3.2.

По схеме единственного деления найти корни системы уравнений

РЕШЕНИЕ

Раздел		x1	x2	x3	Свободные члены	Контрольные ∑	Строчные ∑	ε
Прямой ход	I b1j	3 2 2	2 3 2	2 2 3	13 14 15	20 21 22	20 21 22		0,05 0 0,02
		1	0,67	0,67	4,33	6,67	6,67		0,017
	II b2j		1,66 0,66	0,66 1,66	5,34 6,34	7,66 8,66	7,66 8,66		-0,034 -0,014
			1	0,4	3,22	4,61	4,62		-0,031
	III b3j			1,4	4,2	5,62	5,6		0,006
				1	3	4,01	4,01		0,00014
Обратный ход		1	1	1	3 2,02 0,97			0 -0,02 0,03

х₃=3+0=3; х₂=2,02–0,02=2; х₁=0,97+0,03=1