
- •Руководство к решению задач по алгебре
- •Часть II Жорданова форма матрицы и жорданов базис
- •§1. Собственные векторы и собственные значения оператора.
- •Рассмотрим линейный оператор в пространстве и пусть – матрица этого оператора в некотором базисе .
- •1.2. Алгебраическая и геометрическая кратности собственного значения
- •Жорданова форма матрицы и жорданов базис
- •Алгоритм нахождения жорданова базиса для одной жордановой клетки
- •Алгоритм нахождения жордановой формы и жорданова базиса для матрицы 3-го порядка
- •1.5. Функции от матриц
- •§ 2. Жорданова форма матрицы
- •Оператор простой структуры
Алгоритм нахождения жордановой формы и жорданова базиса для матрицы 3-го порядка
Пусть дана матрица 3-го порядка. Надо найти жорданову форму и жорданов базис.
Пусть характеристический многочлен матрицы имеет вид
![]() ,
где
,
где
![]()
![]() .
.
Тогда
жорданова форма матрицы имеет вид
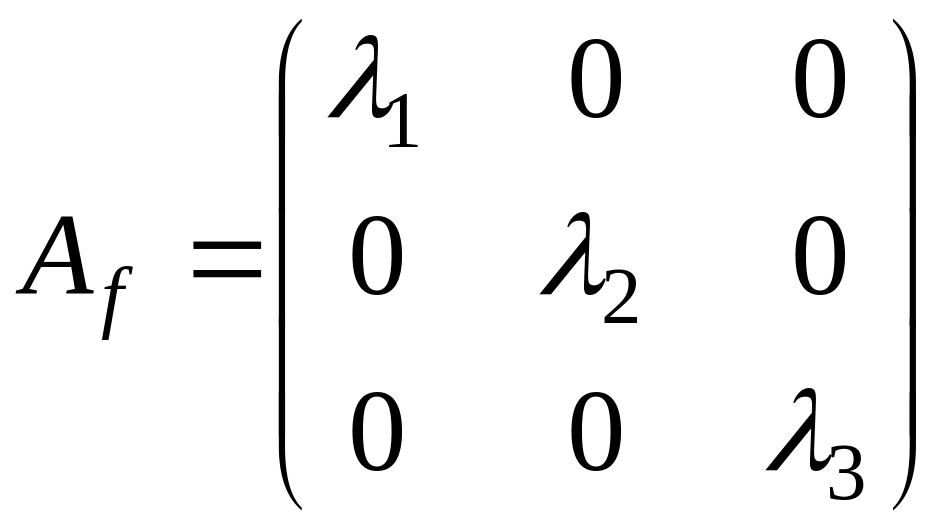 .
.
Пусть характеристический многочлен матрицы имеет вид
![]() ,
,
где . Возможны два случая:
а)
![]() ,
поэтому
,
поэтому
![]() и, следовательно,
и, следовательно,
![]() ,
поэтому жорданова форма содержит две
жордановы клетки с собственным значением
,
поэтому жорданова форма содержит две
жордановы клетки с собственным значением
![]() :
:
 ;
;
б)
![]() ,
поэтому
,
поэтому
![]() и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением
:
и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением
:
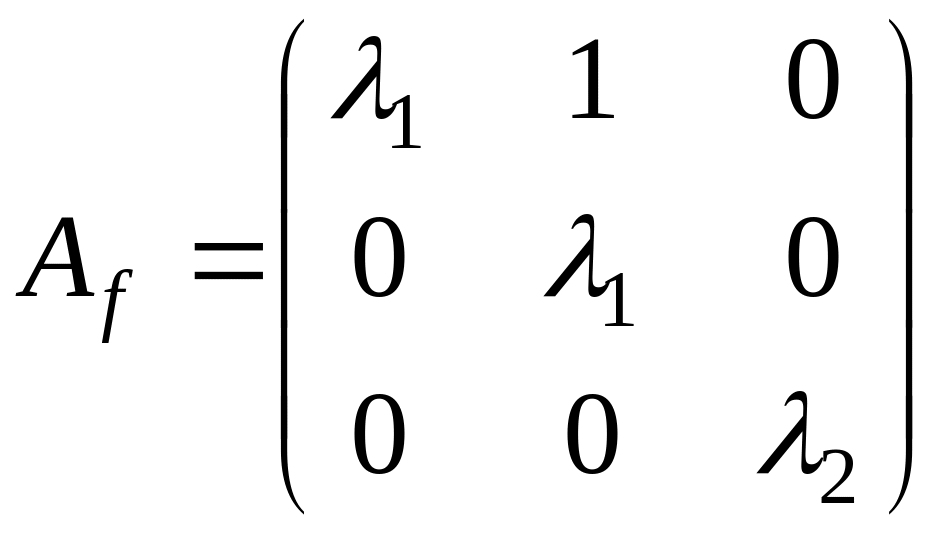 .
.
Пусть характеристический многочлен матрицы имеет вид
![]() .
.
Возможны два случая:
а)
,
поэтому
и, следовательно, жорданова форма
содержит две жордановы клетки с
собственным значением
:
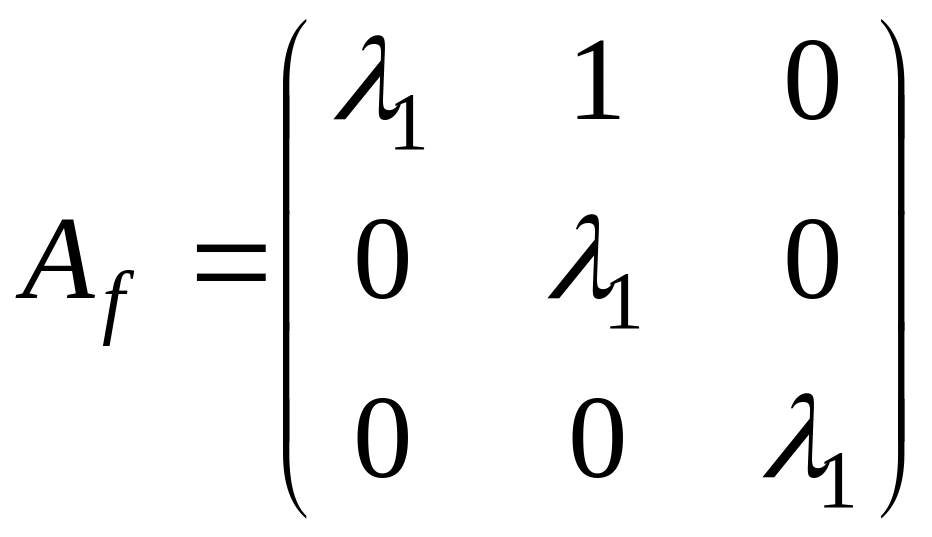 ;
;
б)
,
поэтому
и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением
:
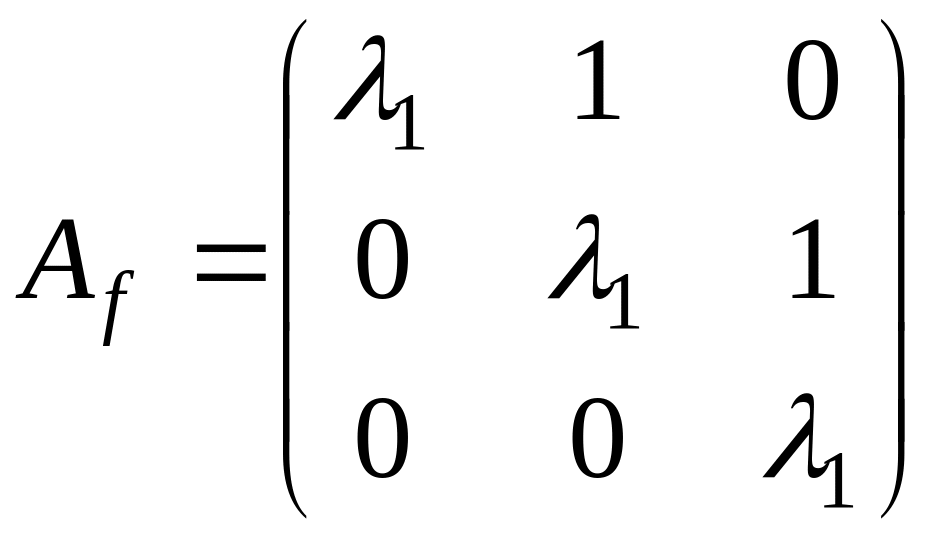 .
.
Задача.
Дана матрица
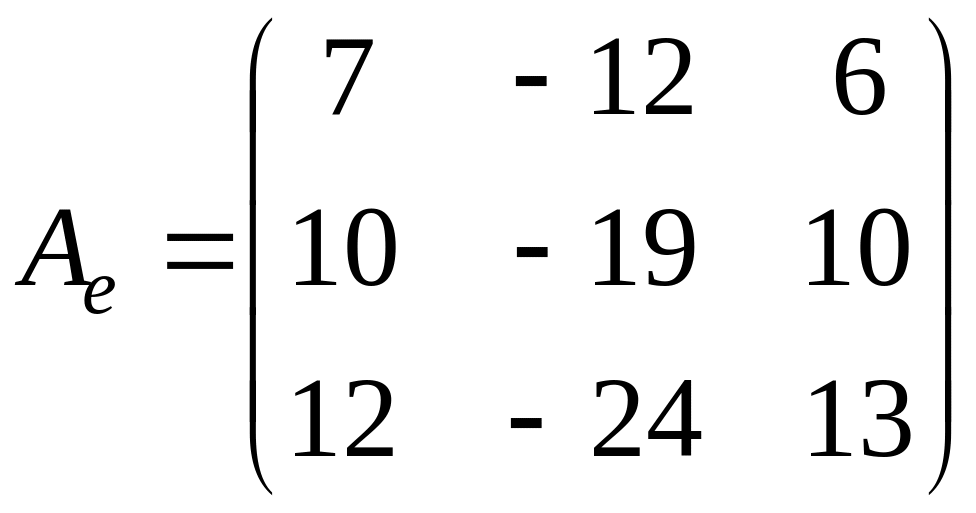 .
Найти
.
Найти
![]() .
.
Р е ш е н и е.
Найдем характеристический многочлен матрицы:
![]() .
.
Жорданова
форма матрицы
имеет вид
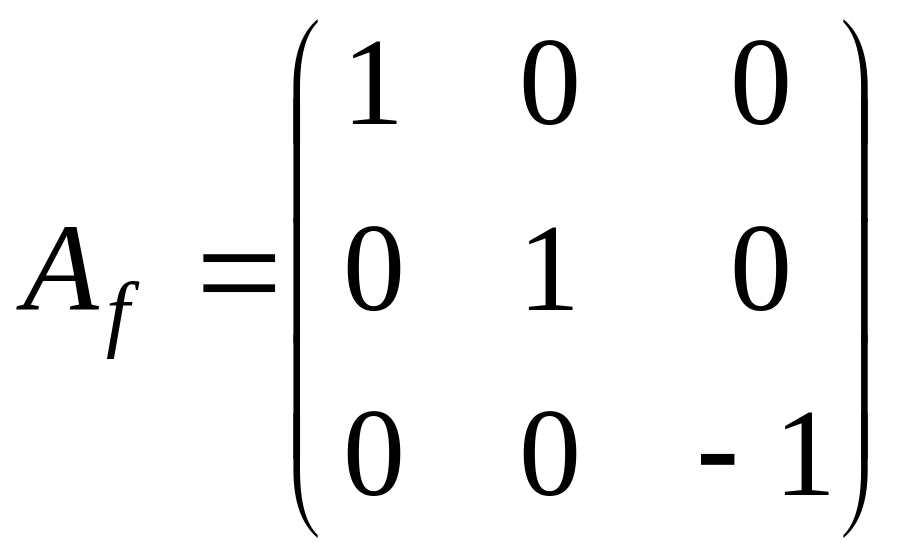 .
.
Найдем
 .
.
Для
нахождения
воспользуемся формулой
![]() ,
где
,
где
![]() – матрица перехода от базиса
– матрица перехода от базиса
![]() к базису
к базису
![]() .
Очевидно, что
.
Очевидно, что
![]() ,
,
поэтому
![]() .
.
Пример 1. Найти жорданову форму и жорданов базис матрицы оператора
 .
.
Р е ш е н и е.
Вычислим
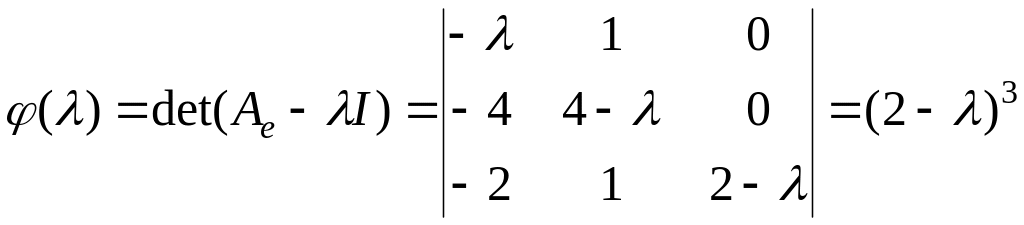 ,
,
следовательно,
собственное значение
![]() ,
,
![]() .
.
Найдем геометрическую кратность собственного значения . Для этого посчитаем ранг матрицы
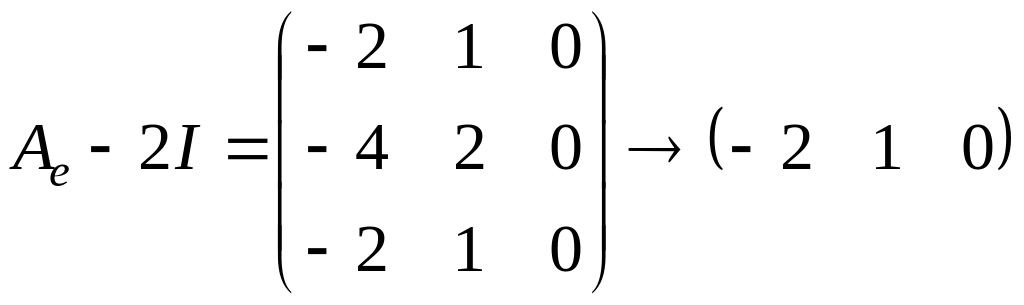 .
.
Следовательно,
![]() ,
,
поэтому жорданова форма имеет вид
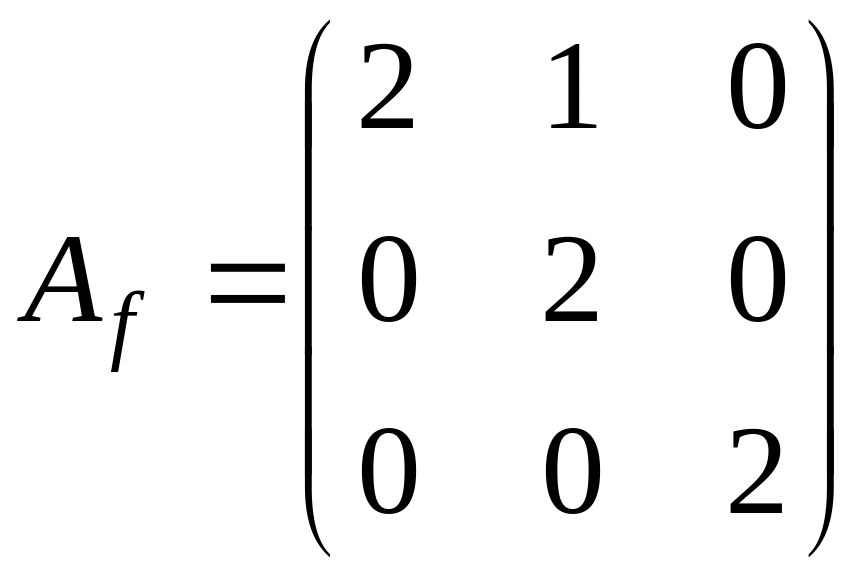 или
или
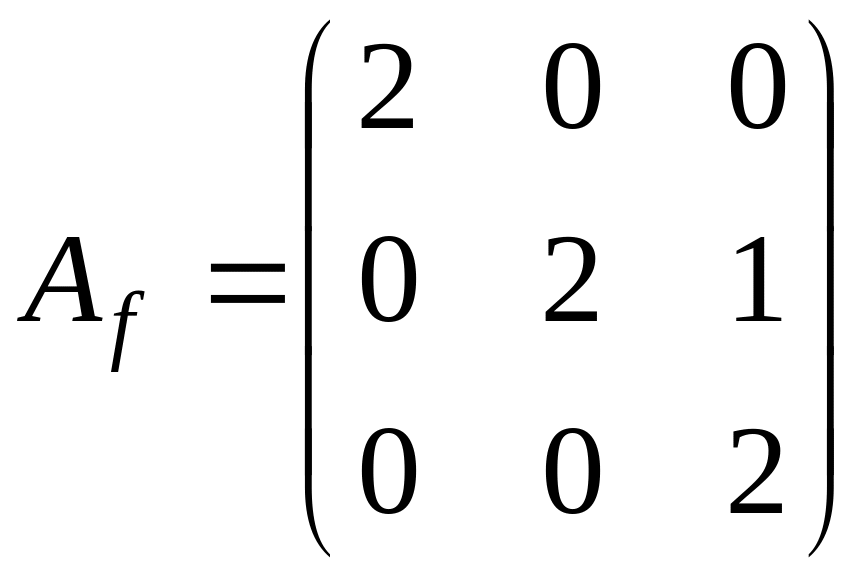 .
.
Найдем собственный вектор , соответствующий собственному значению . Так как он удовлетворяет условию
![]() ,
,
то решим систему
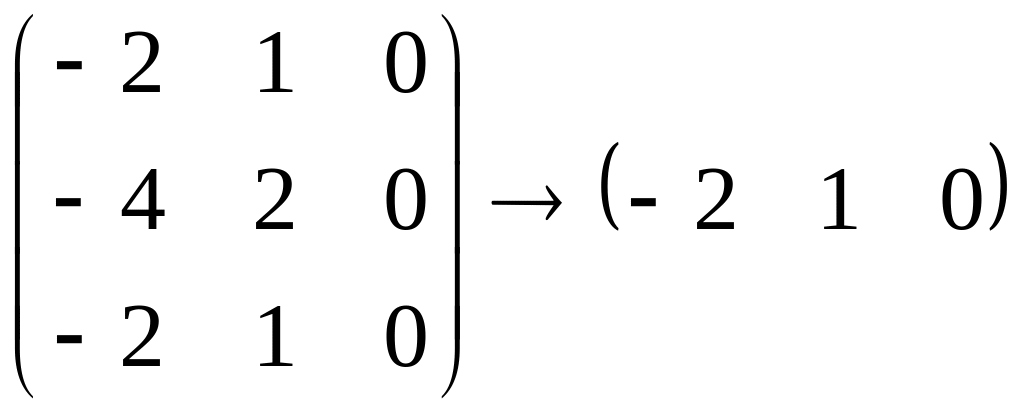 .
.
Следовательно,
координаты собственного вектора
![]() удовлетворяют уравнению
удовлетворяют уравнению
![]() .
.
Заметим, что коэффициент при
![]() равен 0, поэтому
может принимать любые значения.
Отбрасывать
нельзя !!!
равен 0, поэтому
может принимать любые значения.
Отбрасывать
нельзя !!!
Для нахождения ФСР построим таблицу
 .
.
Векторы
![]() ,
,
![]() образуют фундаментальную систему
решений в собственном подпространстве
образуют фундаментальную систему
решений в собственном подпространстве
![]() ,
поэтому любой собственный вектор,
отвечающий собственному значению
,
поэтому любой собственный вектор,
отвечающий собственному значению
![]() ,
линейно через них выражается и,
следовательно, имеет вид
,
линейно через них выражается и,
следовательно, имеет вид
![]() .
Так как
.
Так как
![]() ,
,
то должен быть один присоединенный
вектор, который будет являться решением
системы
,
,
то должен быть один присоединенный
вектор, который будет являться решением
системы
![]() .
Подберем коэффициенты
.
Подберем коэффициенты
![]() и
и
![]() таким образом, чтобы система
была совместна. Так как
таким образом, чтобы система
была совместна. Так как
 ,
,
то для
совместности системы необходимо, чтобы
выполнялось условие
![]() .
Возьмем
.
Возьмем
![]() ,
тогда
,
тогда
![]() ,
и координаты присоединенного вектора
являются решением системы
,
и координаты присоединенного вектора
являются решением системы
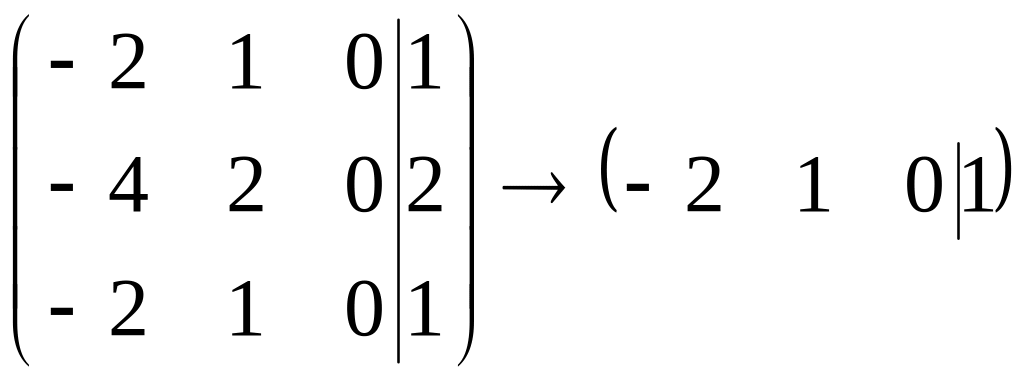 ,
,
то есть удовлетворяют уравнению
![]() или
или
![]() .
.
Возьмем
![]() .
.
Таким образом, у нас есть собственный
вектор
![]() ,
присоединенный к нему
,
присоединенный к нему
![]() и нужен еще один собственный вектор,
отвечающий собственному значению
.
Можно взять или вектор
и нужен еще один собственный вектор,
отвечающий собственному значению
.
Можно взять или вектор
![]() ,
или
,
или
![]() ,
или любой другой, отличный от
,
отвечающий собственному значению
.
Эти три вектора и будут образовывать
жорданов базис.
,
или любой другой, отличный от
,
отвечающий собственному значению
.
Эти три вектора и будут образовывать
жорданов базис.
Пример 2. Найти жорданову форму и жорданов базис матрицы оператора
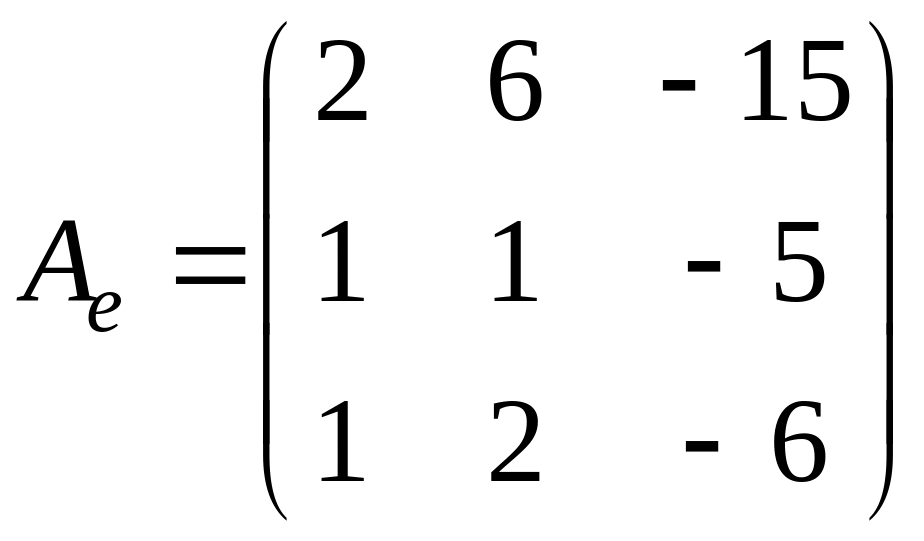 .
.
Р е ш е н и е.
Вычислим
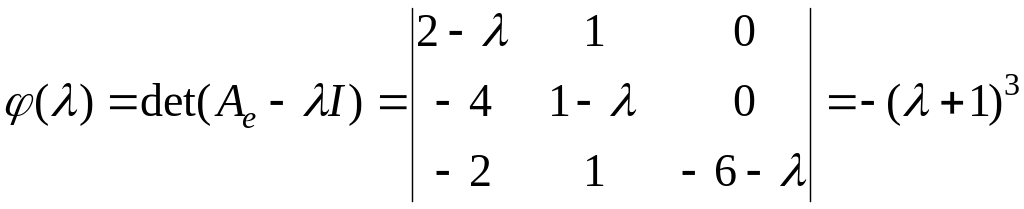 ,
,
следовательно,
собственное значение
![]() ,
.
,
.
Найдем геометрическую кратность собственного значения . Для этого посчитаем ранг матрицы
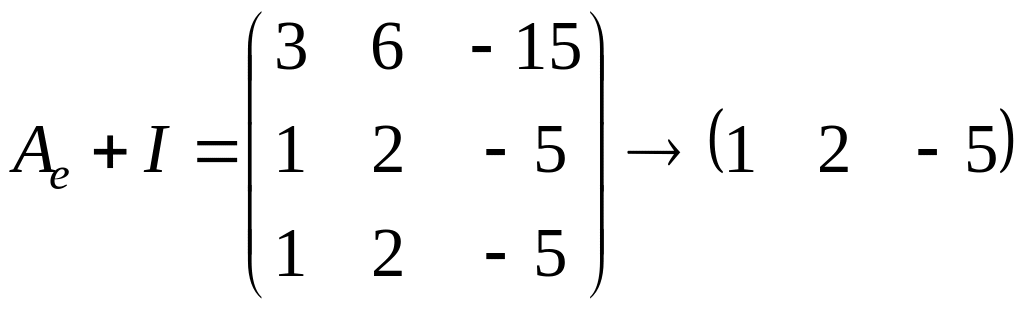 .
.
Следовательно,
![]() ,
,
поэтому жорданова форма имеет вид
 или
или
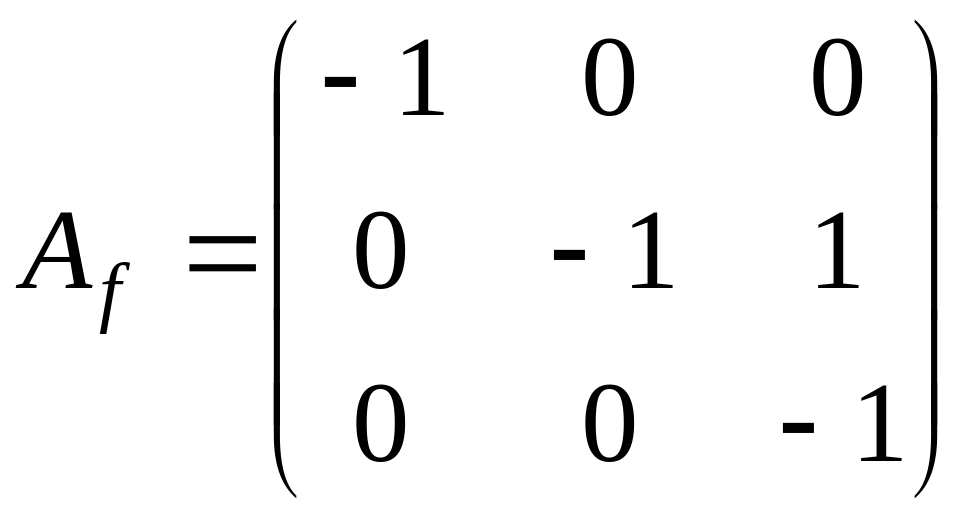 .
.
Найдем собственный вектор , соответствующий собственному значению . Так как он удовлетворяет условию
![]() ,
,
то решим систему
 .
.
Очевидно, что координаты собственного вектора удовлетворяют уравнению
![]() или
или
![]() .
.
Для нахождения ФСР построим таблицу
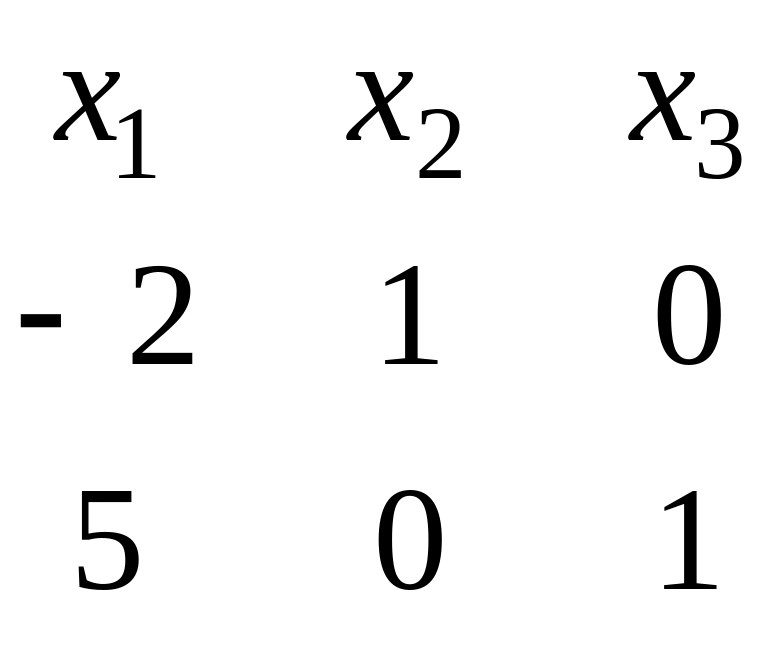 .
.
Векторы
![]() ,
,
![]() образуют фундаментальную систему
решений в собственном подпространстве
образуют фундаментальную систему
решений в собственном подпространстве
![]() ,
поэтому любой собственный вектор,
отвечающий собственному значению
,
поэтому любой собственный вектор,
отвечающий собственному значению
![]() ,
линейно через них выражается
и, следовательно, имеет вид
,
линейно через них выражается
и, следовательно, имеет вид
![]() .
.
Так как
,
,
то должен быть один присоединенный
вектор, который будет являться решением
системы
![]() .
Подберем коэффициенты
и
таким образом, чтобы система
была совместна. Так как
.
Подберем коэффициенты
и
таким образом, чтобы система
была совместна. Так как
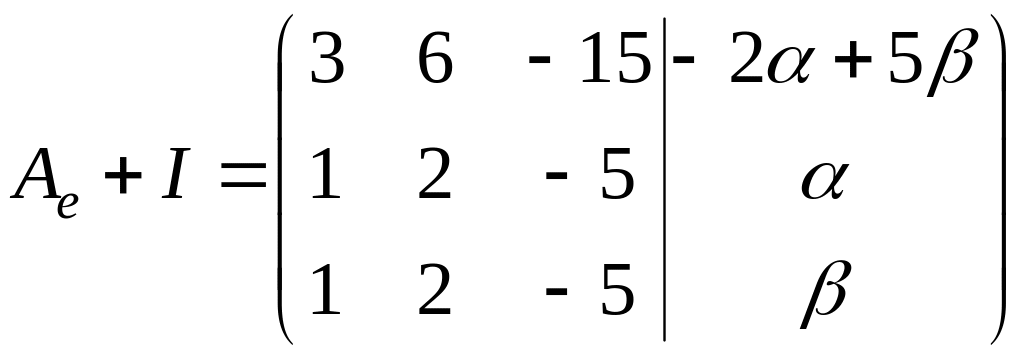 ,
,
то для
совместности системы необходимо, чтобы
выполнялось условие
.
Возьмем
,
тогда
![]() и координаты присоединенного вектора
являются решением системы
и координаты присоединенного вектора
являются решением системы
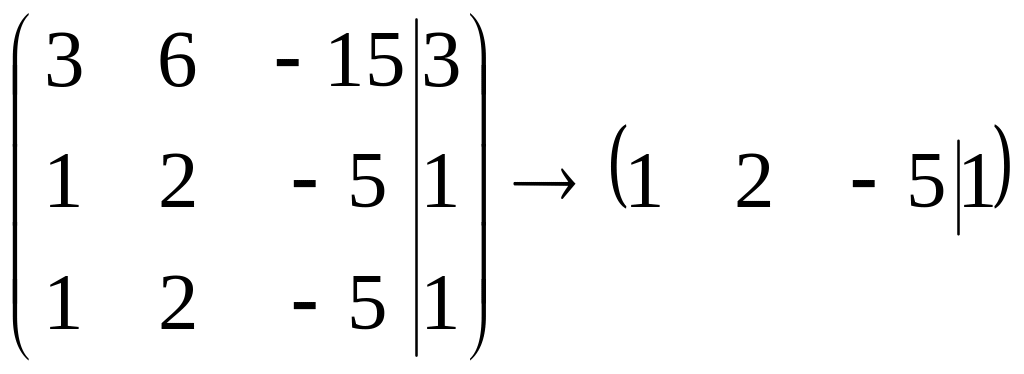 ,
,
то есть удовлетворяют уравнению
![]() или
или
![]() .
.
Возьмем
![]() .
.
Таким образом, у нас есть собственный вектор , присоединенный к нему и нужен еще один собственный вектор, отвечающий собственному значению . Можно взять или вектор , или , или любой другой, отличный от , отвечающий собственному значению . Эти три вектора и будут образовывать жорданов базис.
Пример 3. Найти жорданову форму и жорданов базис матрицы оператора
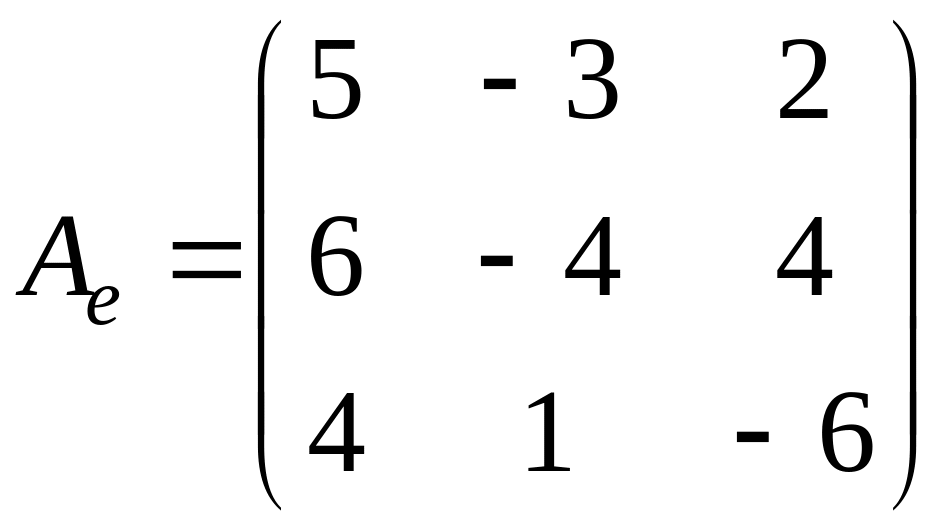 .
.
Р е ш е н и е.
Вычислим
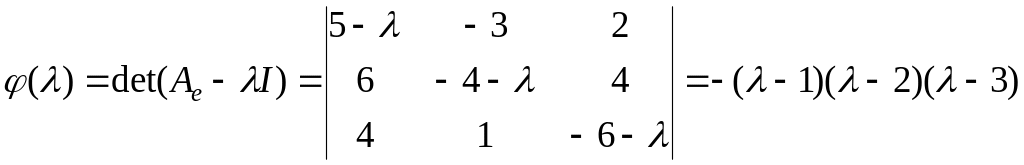 .
.
Таким образом, получили три собственных
значения
![]() ,
,
![]() ,
,
![]() .
Так как алгебраическая кратность каждого
из них равна 1, то жорданова форма имеет
следующий вид
.
Так как алгебраическая кратность каждого
из них равна 1, то жорданова форма имеет
следующий вид
 .
.
Найдем собственный вектор
![]() ,
соответствующий собственному значению
.
Очевидно, что он является решением
уравнения
,
соответствующий собственному значению
.
Очевидно, что он является решением
уравнения
![]() и, следовательно, его координаты
удовлетворяют системе
и, следовательно, его координаты
удовлетворяют системе
![]()
![]() ,
,
то есть
![]() ,
поэтому можем взять
,
поэтому можем взять
![]() .
.
Вычислим собственный вектор
![]() ,
соответствующий собственному значению
.
Очевидно, что он удовлетворяет уравнению
,
а его координаты – системе
,
соответствующий собственному значению
.
Очевидно, что он удовлетворяет уравнению
,
а его координаты – системе
 ,
,
откуда
следует, что
![]() ,
поэтому можем взять
,
поэтому можем взять
![]() .
.
Найдем собственный вектор
![]() ,
соответствующий собственному значению
,
соответствующий собственному значению
![]() .
Так как он является решением уравнения
.
Так как он является решением уравнения
![]() ,
то его координаты удовлетворяют системе
,
то его координаты удовлетворяют системе
![]()
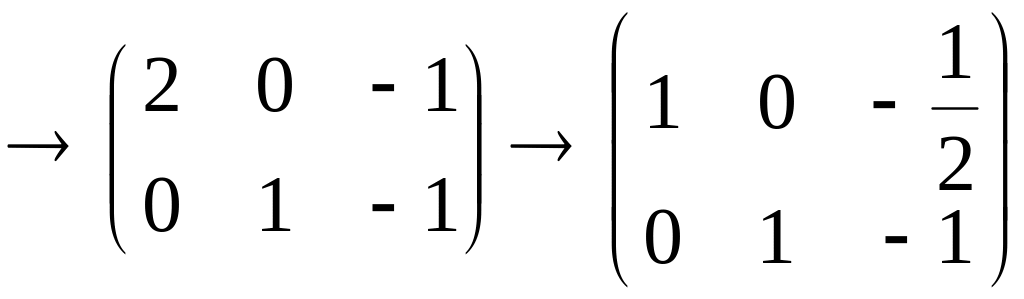 ,
,
и,
следовательно,
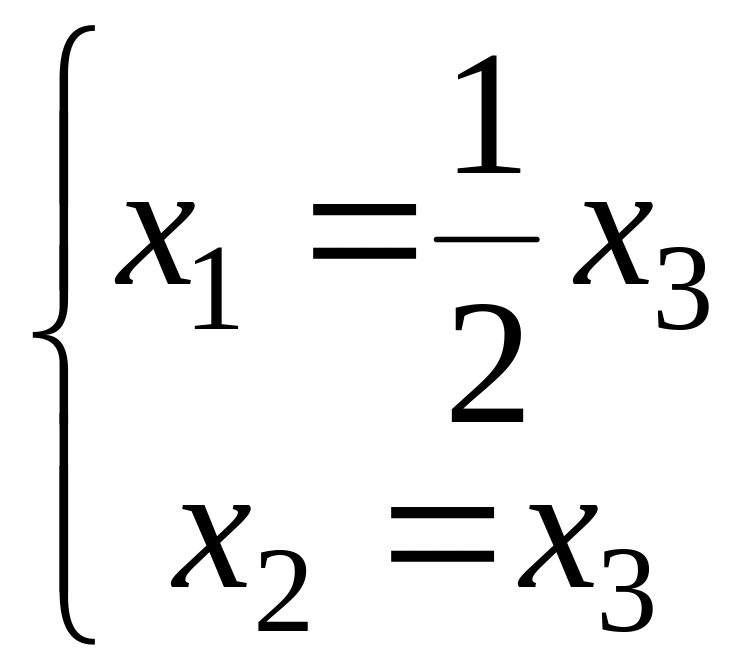 ,
поэтому можем взять
,
поэтому можем взять
![]() .
.
Векторы
![]() образуют жорданов базис матрицы.
образуют жорданов базис матрицы.
Пример 4. Найти жорданову форму и жорданов базис матрицы оператора
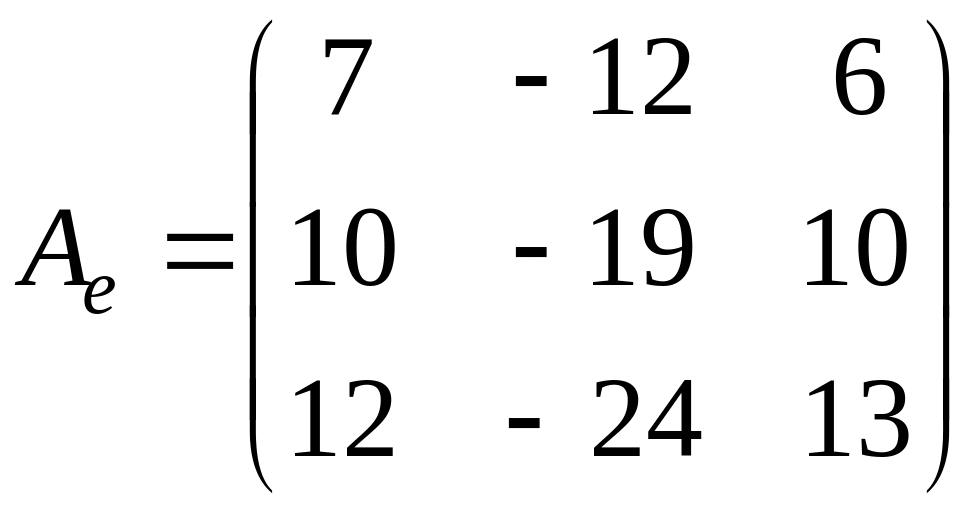 .
.
Р е ш е н и е.
Вычислим
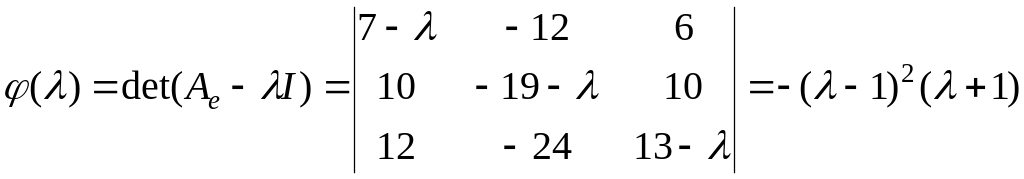 .
.
Таким образом, получили два собственных
значения
,
![]() .
Так как алгебраическая кратность
равна 2, нужно вычислить геометрическую
кратность
.
Так как алгебраическая кратность
равна 2, нужно вычислить геометрическую
кратность
![]() собственного значения
.
Для этого посчитаем ранг матрицы
собственного значения
.
Для этого посчитаем ранг матрицы
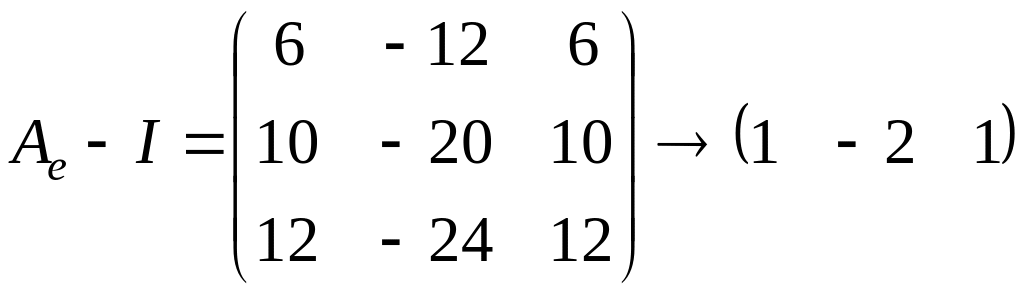 .
.
Очевидно, что
![]() ,
поэтому
,
поэтому
![]() и, следовательно, жорданова форма имеет
следующий вид
и, следовательно, жорданова форма имеет
следующий вид
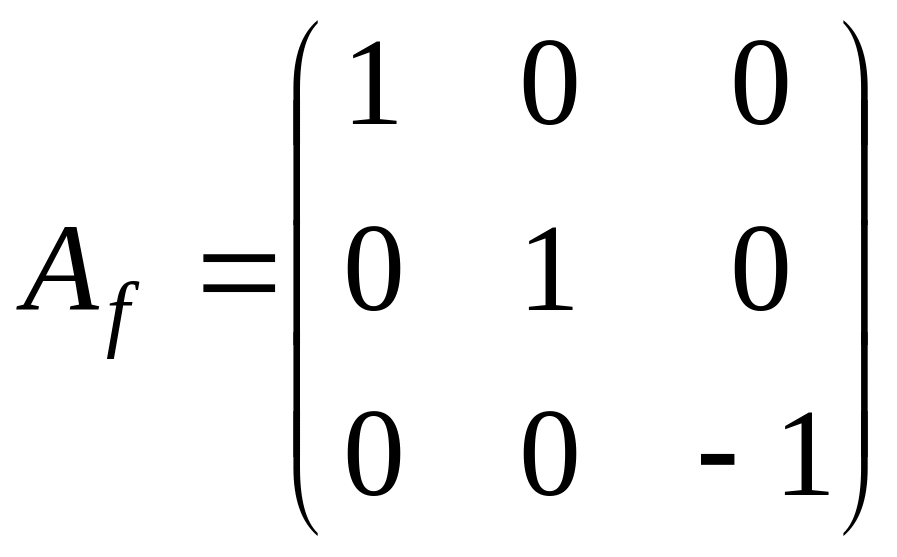 .
.
Найдем собственные векторы
,
,
соответствующие собственному значению
.
Очевидно, что они являются решением
уравнения
,
а их координаты
![]() – решением системы
– решением системы
 ,
,
и, следовательно, удовлетворяют уравнению
![]() или
или
![]() .
.
Для нахождения ФСР построим таблицу
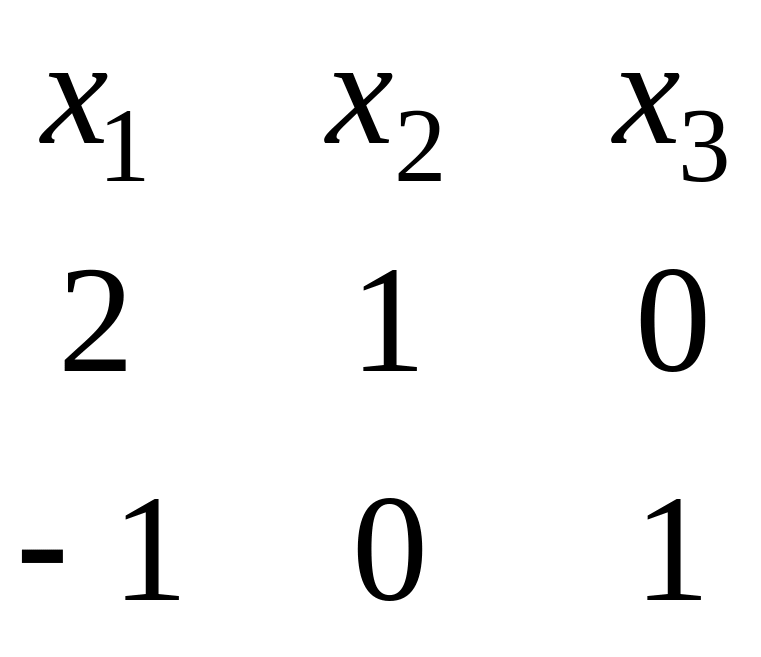 .
.
Векторы
![]() ,
,
![]() образуют фундаментальную систему
решений в собственном подпространстве
образуют фундаментальную систему
решений в собственном подпространстве
![]() ,
поэтому любой собственный вектор,
отвечающий собственному значению
,
поэтому любой собственный вектор,
отвечающий собственному значению
![]() ,
линейно через них выражается и,
следовательно, имеет вид
,
линейно через них выражается и,
следовательно, имеет вид
![]() .
.
Так
как
,
то нужно выбрать любые два линейно
независимых вектора из этой линейной
комбинации. Возьмем
![]() ,
,
![]() .
.
Найдем собственный вектор , соответствующий собственному значению . Очевидно, что он удовлетворяет уравнению , а его координаты – системе
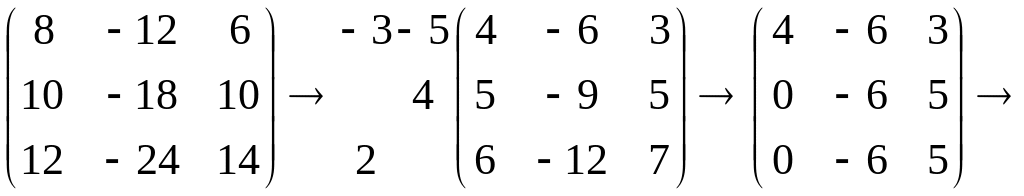
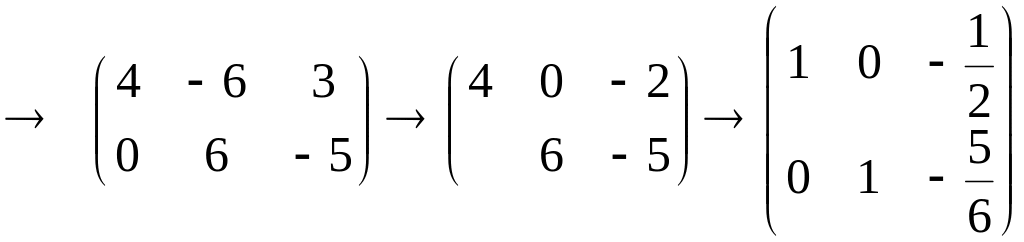 ,
,
то есть
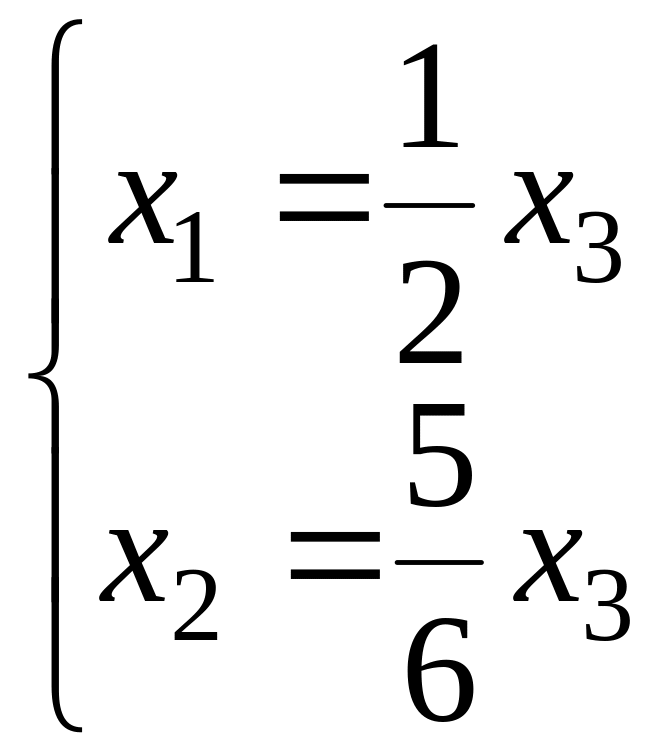 ,
поэтому можем взять
,
поэтому можем взять
![]() .
.
Векторы образуют жорданов базис матрицы.
