Глава 1. Элементы теорий множеств

О числах

1. «Натуральные числа» (естественные числа) это числа, возникающие естественным путем при счёте (при нумеровании предметов или при обозначении количества предметов). Множество всех натуральных чисел (1, 2, 3, …, n, …) обозначают символом N.

Из множества натуральных чисел можно выделить особые подмножества: это «простые числа», «числа Фибоначчи».

Простое число – это такое натуральное число (больше единицы), которое не делится ни на одно другое число (кроме самого себя и единицы) без остатка. Например, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71 и т.д.

В 1742 г. прусский математик Кристиан Гольдбах в письме к Леонарду Эйлеру высказал свое предположение (гипотезу): «каждое нечетное число больше 5-и можно представить в виде суммы трех простых чисел» - называется тернарной проблемой Гольдбаха. Эйлер выдвинул боле сильную гипотезу: каждое четное число большее 2 можно представить в виде суммы двух простых чисел» - называется проблемой Эйлера.

Числа Фибоначчи.

Леонардо Пизанский (1170-1250) изучал всю арабскую литературу о математике и проложил начало использования десятичной системы счисления в Европе.

Числовой ряд, в котором каждое последующее число равно сумме двух предыдущих, в честь ученого носит название чисел Фибоначчи:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,144, 233, 377, 610, 987, 1597, 2584, 4181 и т.д.

Хотя этот ряд чисел давно был известен в Древней Индии (на родине чисел десятичной системы), но благодаря исследованиям свойств этих чисел они носят название числа Фибоначчи.

Чудесное устройство, красота и гармония природы можно заметить в волнах океанов, в лепестках цветов, вообще в растениях и животных, в ракушках и даже микроорганизмах. И во всем этом кроется нечто общее – математическая гармония устройства мироздания, суммационная последовательность чисел Фибоначчи.

В 13 веке Фома Аквинский (1225-1274, итальянский философ, теолог сформулировавши пять доказательств бытия Бога) сформулировал один из основных принципов эстетики - чувствам человека приятны объекты, обладающие правильными пропорциями. Он ссылался на прямую связь между красотой и математикой, которую нередко можно "измерить" и найти в природе. В инстинктах человека заложена позитивная реакция на правильные геометрические формы, как в окружающей природе, так и в рукотворных объектах, таких, как произведения живописи. Гармония в пропорциях нужна человеку для удовлетворения его потребности в комфорте. Фома Аквинский ссылался на тот же принцип, что открыл Фибоначчи.

 Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (13:8, 21:13 или 5:3), получим число, колеблющаяся около иррационального значения 1,61803398875... (и через раз то превосходящая, то не достигающая его). Для краткости это иррациональное число пишут в виде 1,618 и обозначают греческой буквой Ф. Средневековый математик Лука Пачиоли назвал это соотношение Божественной пропорцией, известны также названия Золотое сечение, Золотое среднее.

Золотое сечение - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

Кеплер (1571-1630, немецкий математик, астроном) назвал это соотношение «одним из сокровищ геометрии». Интересно, что квадрат любого числа Фибоначчи равен числу, стоящему перед ним, умноженному на число, стоящее после него и плюс или минус единице:

5²=3х8+1; 8²= 5х13-1; 13²=8х21+1 и т.д.

Не будет преувеличением сказать, что это не просто игра с числами, а важное математическое выражение природных явлений. Приводимые ниже примеры показывают некоторые интересные приложения.

Исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1,618 играет центральную роль.  Пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты. Не только египетские пирамиды построены в соответствии с совершенными пропорциями золотого сечения (Ф=1,618), то же самое явление обнаружено и у мексиканских пирамид. Возникает мысль, что как египетские, так и мексиканские пирамиды были возведены приблизительно в одно время людьми общего происхождения.

Другое проявление чисел Фибоначчи наблюдается в числе пазух на стебле растения во время его роста, в количестве лепестков цветов (Ирис 3 лепестка, Примула 5, Амброзия 13, Нивяник обыкновенный 34, Астра 55 и 89) и т.д.

Волны Эллиотта. Ральф Нельсон Эллиотт был инженером. После серьезной болезни в начале 1930-х г.г. он занялся анализом биржевых цен, особенно индекса Доу-Джонса. Согласно наблюдениям Эллиотта, движения индекса Доу-Джонса подчиняются определенным ритмам, следуя тому же закону, что и приливы - отливы, за действием (акцией) следует противодействие (реакция).  Он писал: "Любой человеческой деятельности присущи три отличительных особенности: форма, время и отношение, и все они подчиняются суммационной последовательности Фибоначчи".

2. «Целое число» - если к натуральным числам добавить 0 и их «зеркальное отображение», т.е. их минусовые значения, то получим семейство целых чисел, что обозначают символом Z. Z = {…, -2, -1, 0, 1, 2, 3, …, n, …}. На множестве целых чисел определяются арифметические операции сложении (+) и вычитания (-).

3. «рациональное число» - число, которое представляется в виде несократимой обыкновенной дроби m/n, где m целое число, а n натуральное число, т.е. является результатом деления m на n. Множество рациональных чисел обозначают символом Q и символически представляют в виде Q = {m/n, m Z, n N}. Численно равные дроби (как, например, 3/4 и 9/12) входят в это множество как одно число.

4. «иррациональное число» - это такое вещественное число, которое невозможно представить в виде рациональной дроби m/n. В десятичной форме у иррационального числа после чисел целой части (после запятой) стоят бесконечное количество чисел, не повторяющихся каким либо порядком. О них знали в Древнем Египте, Вавилоне и Греции. Геометрически это означало несоизмеримость длины отрезка с отрезком единичной длины. Например, у квадрата со стороной 1 диагональ (равна ), несоизмерима с 1. Семейство иррациональных чисел обозначают символом I.

Понятно, что семейство рациональных чисел включает в себе семейство целых чисел, а семейство целых чисел включает в себе семейство натуральных чисел. Рациональные и иррациональные числа вместе составляют семейство «действительных (вещественных) чисел», что обозначается символом R.

5) . «Комплексные числа» - Комплексным числом z называется упорядоченная пара (х,y) действительных чисел, где первая компонента х называется действительной частью z и обозначают через Rez, а вторая компонента y - мнимой частью Imz.

Комплексные числа z₁=(x₁,y₁) и z₂=(x₂,y₂) равны, если равны их действительные и мнимые части. На множестве комплексных чисел определены операции сложения и умножения:

(x₁,y₁) + (x₂,y₂) = (х₁ + х₂, y₁ + y₂); z₁z₂=(x₁,y₁)(x₂,y₂) = (x₁x₂ – y₁y₂, x₁y₂ + x₂y₁).

Вычитание и деление комплексных чисел определяются как действия, обратные сложению и умножению соответственно. Полем комплексных чисел называют все множество комплексных чисел с определенными выше операциями над ними и обозначают символом С. Число (0,0) является нулем, а число (1,0) – единицей этого поля. Число (0,1) называется мнимой единицей и обозначается символом i. Из определения следует, что i² = -1. Алгебраической формой комплексного числа z называют его такое представление: z =(x,y) = x + iy, а геометрически z это точка с координатами (х,y) на декартовой поле. Число ͞z = x – iy называется сопряженным с числом z = x + iy. Геометрически z и ͞z , как точки, расположены симметрично относительно оси ОХ. Модулем комплексного числа z называют действительное число |z| = 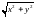,что есть расстояние от этой точки до начала системы (0,0).

Пример 1. Решить уравнение z³-z²+z-1=0.

Разложим полином (многочлен) третьего порядка на множители:

z³-z²+z-1 = z²(z-1) + z-1 = (z-1)(z²+1) = 0, следует z-1=0 или z²+1= 0, откуда и получаем один действительный корень z₁ =1 и два комплексных: z₂= i и z₃= -i.