2.6. Цифровой резонатор

Цифровой резонатор (рисунок 2.11) представляет собой звено второго порядка, у которого коэффициенты системной функции B₁ и B₂ равны нулю, а коэффициент B₀=1.

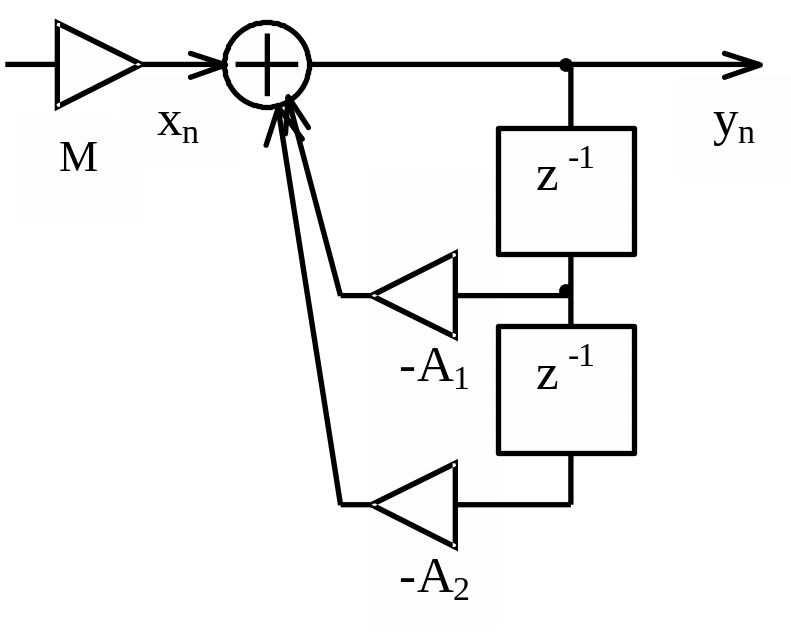
Рисунок 2.11 – Цифровой резонатор

Масштабный коэффициент на входе фильтра M предотвращает появление значений сигналов резонатора, выходящих за пределы разрядной сетки вычислительного устройства, на котором он реализован.

Системная функция резонатора описывается следующим соотношением

. (2.13)

Определим полюсы системной функции. Для этого приравняем знаменатель нулю и найдем корни полученного квадратного уравнения

,

.

В цифровом резонаторе полюсы системной функции должны быть комплексно-сопряжёнными. В противном случае (2.13) представляет собой системную функцию фильтра нижних частот.

Следовательно, должно выполняться условие

.

При этом условии полюсы системной функции определяются следующим соотношением

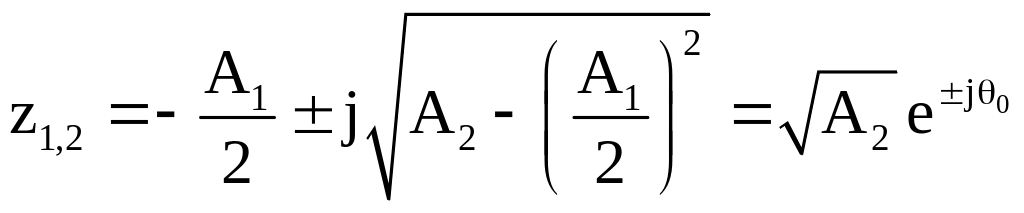, (2.14)

где .

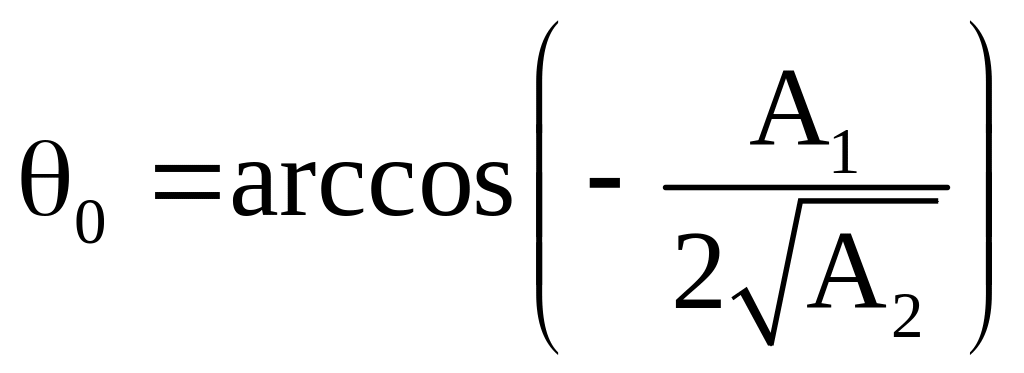На рисунке 3.11 показаны полюсы системной функции резонатора на комплексной плоскости z. Окружность единичного радиуса с центром в начале координат является геометрическим местом точек, для которых выполняется условие

.

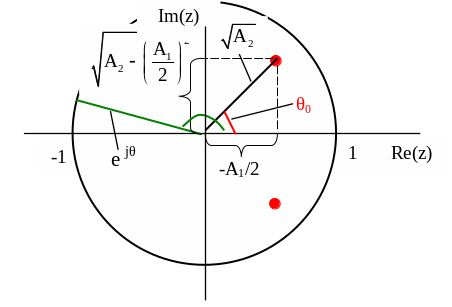
Рисунок 2.12 – Полюсы системной функции z₁ и z₂

При изменении θ от 0 до π частота изменяется от 0 до F_Д / 2. При этом конец вектора перемещается по окружности единичного радиуса. Расстояние конца этого вектора от полюса системной функции минимально при , т.е. при , где - резонансная частота резонатора.

Подставляя в последнее соотношение θ₀ из (2.14), получим

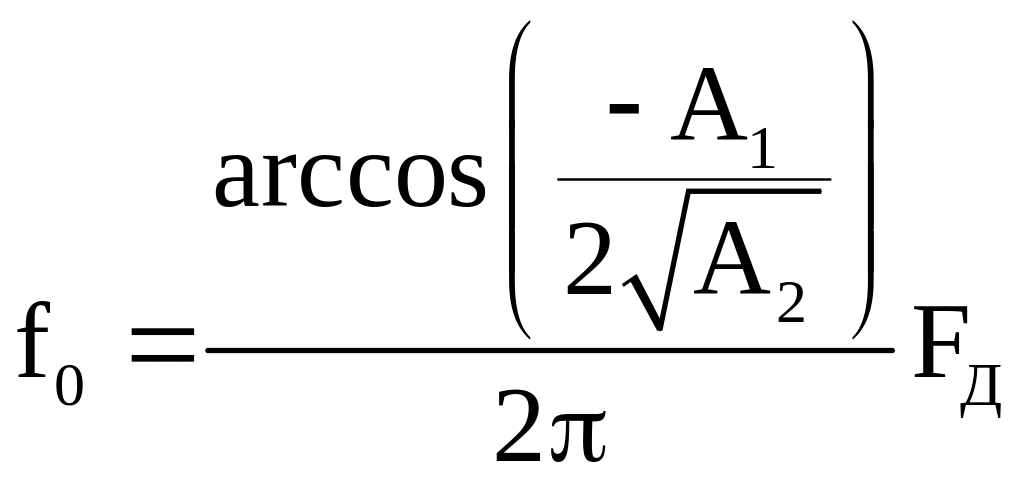. (2.15)

Из последнего соотношения видно, что резонансная частота зависит от частоты дискретизации F_Д и коэффициентов системной функции A₁ и A₂. При A₁=0 резонансная частота равна четверти частоты дискретизации, при A₁<0 резонансная частота меньше четверти частоты дискретизации, а при A₁> 0 – больше четверти частоты дискретизации.

Определим комплексный коэффициент передачи резонатора при A₁=0.

Подставляя в (2.13) , получим

.

Последнее соотношение позволяет определить АЧХ и ФЧХ резонатора:

, (2.16)

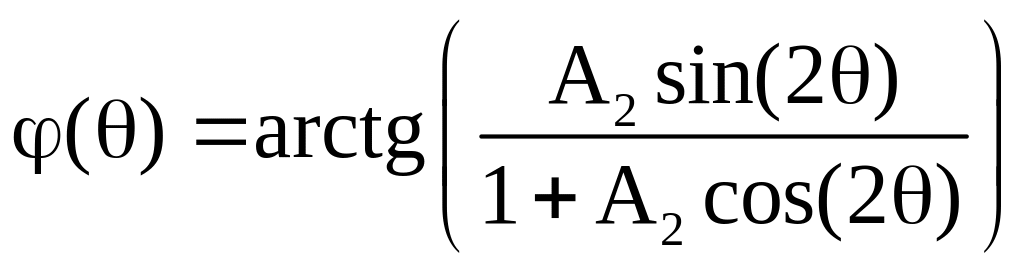. (2.17)

Из (2.16) видно, что на резонансной частота при резонансный коэффициент передачи равен

. (2.18)

На рисунке 2.13 приведена АЧХ, рассчитанная по (2.16), а на рисунке 2.14 – ФЧХ, рассчитанная по (2.17) при A₂=0.9, M=1-A₂. АЧХ и ФЧХ при A₂=0.99 приведены на рисунках 2.15 и 2.16 соответственно.

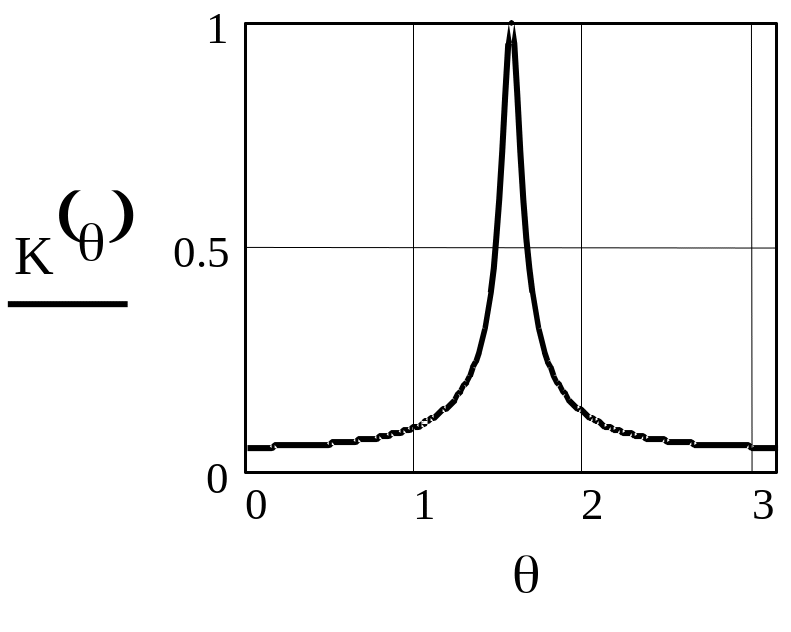
Рисунок 2.13 -АЧХ резонатора при =0.9, =0, M=1-

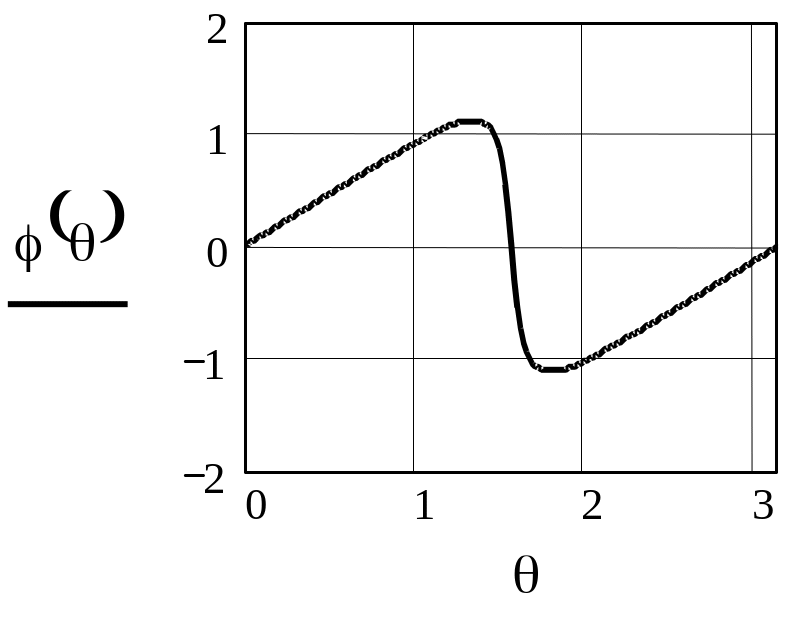
Рисунок 2.14 -ФЧХ резонатора при =0.9, =0

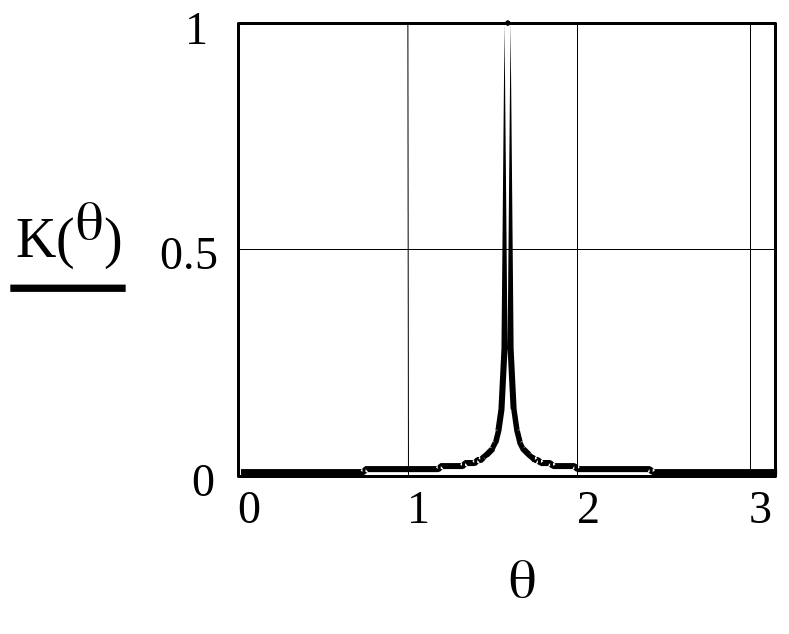
Рисунок 2.15 -АЧХ резонатора при =0.99, =0, M=1-

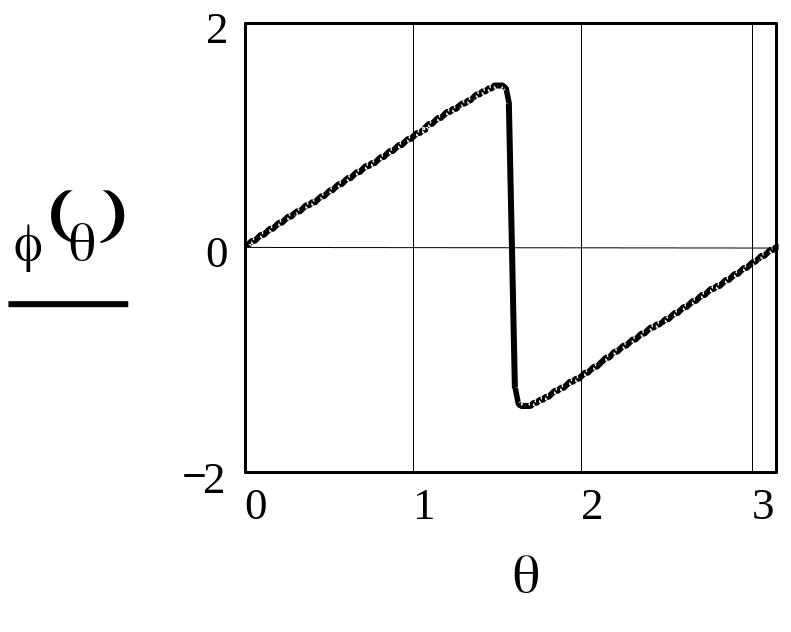
Рисунок 2.16 -ФЧХ резонатора при =0.99, =0

Из приведенных графиков видно, что АЧХ цифрового резонатора по форме похожа на резонансную кривую аналогового колебательного контура, а ФЧХ резонатора отличается от ФЧХ аналогового контура тем, что стремится к нулю при больших расстройках относительно резонансной частоты. Вблизи резонансной частоты ФЧХ цифрового резонатора подобна ФЧХ аналогового колебательного контура.

Сравнение характеристик при разных значениях коэффициента А₂ показывает, что при стремлении А₂ к единице полоса пропускания резонатора уменьшается (резонанс становится более острым) и увеличивается крутизна ФЧХ вблизи резонансной частоты.

Для выяснения влияния коэффициента А₁ на свойства резонатора рассмотрим АЧХ и ФЧХ при А₁<0 и при A₁>0. Соответствующие графики приведены на рисунках 2.17 .. 2.20.

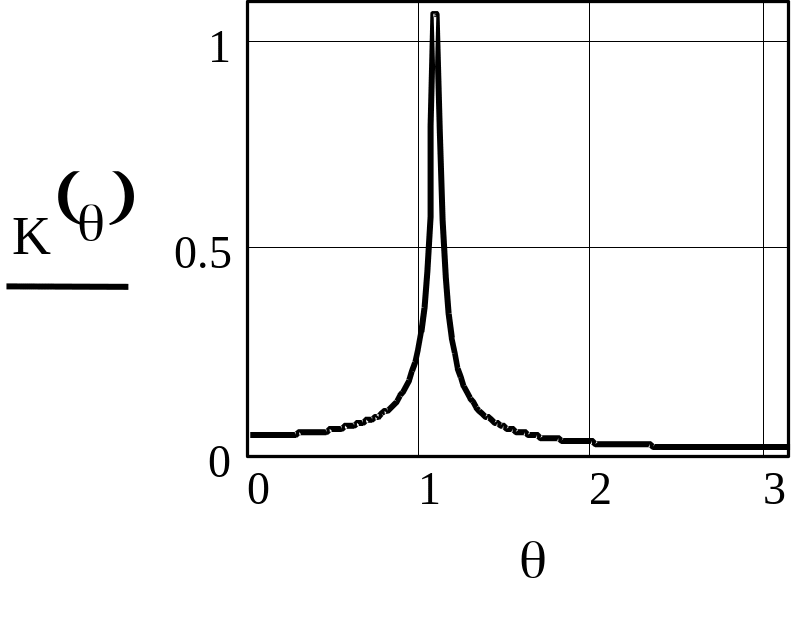
Рисунок 2.17 - АЧХ резонатора при =0.9, = -0.9, M=1-

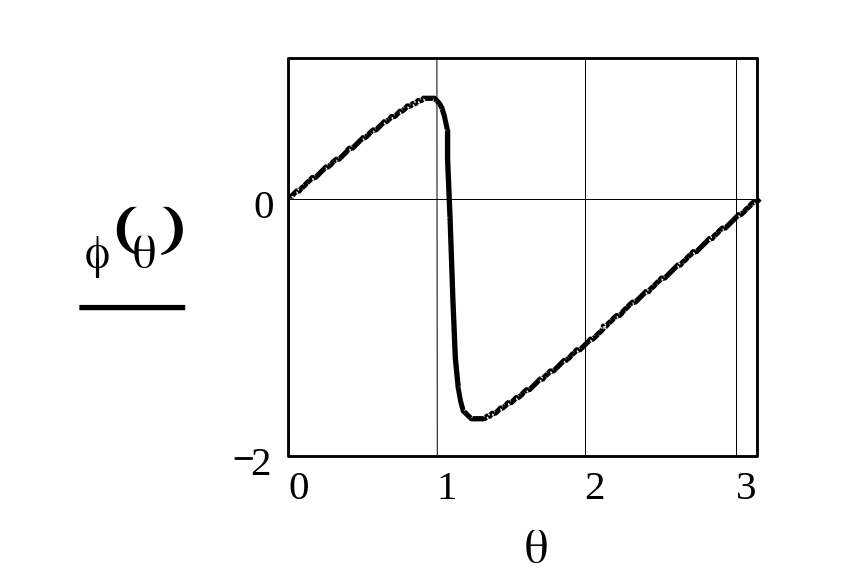
Рисунок 2.18 -ФЧХ резонатора при =0.9, = -0.9

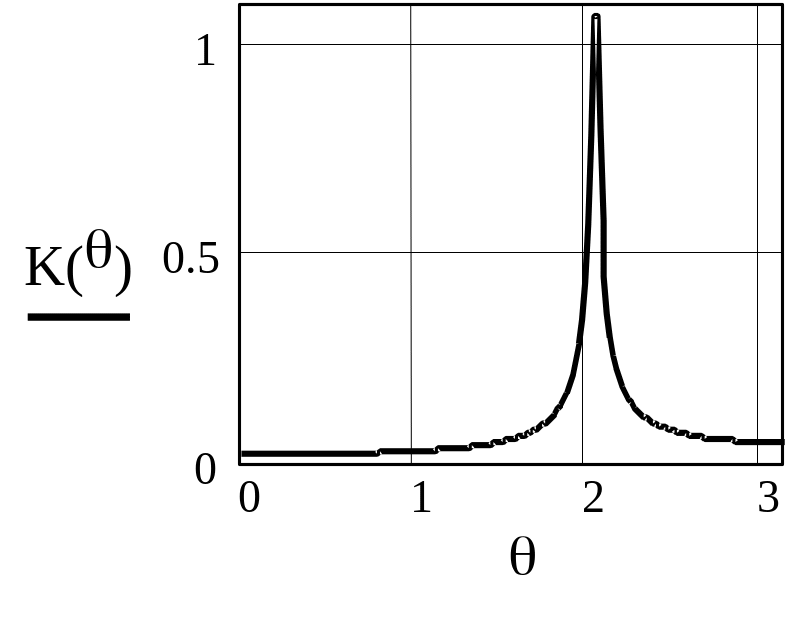
Рисунок 2.19 - AЧХ резонатора при =0.9, = 0.9, M=1-

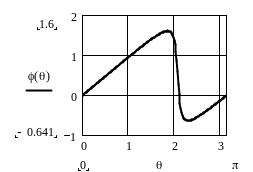
Рисунок 2.20 - ФЧХ резонатора при =0.9, =0.9

Из приведенных рисунков видно, что коэффициент А₁ сильно влияет на резонансную частоту резонатора. В результате АЧХ и ФЧХ сдвигаются вдоль оси частот. При этом нарушается симметрия АЧХ, становятся различными абсолютные значения максимального и минимального фазового сдвигов, вносимых резонатором, изменяется максимальное значение коэффициента передачи.