1.5. Алгебраические дополнения и миноры

Вернемся к вычислению определителя третьего порядка по формуле (1.13):

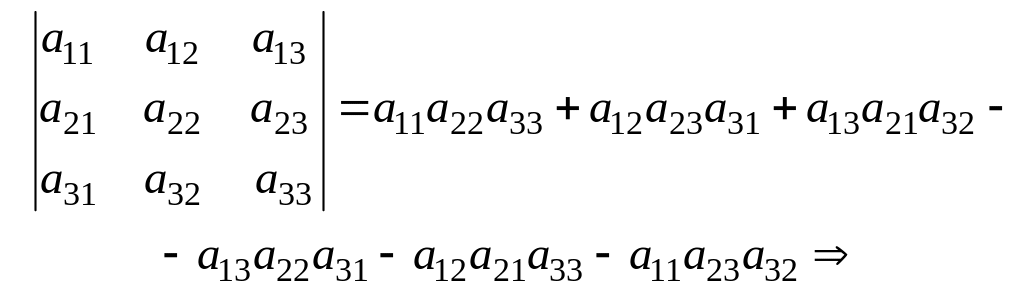(1.16)

Сгруппируем члены правой части выражения (1.16), содержащие элементы первой строки определителя, и вынесем эти элементы за скобки:

(1.17)

Выражения в скобках будем называть алгебраическими дополнениями элементов первой строки определителя и обозначать большими буквами с теми же индексами. Выражение (1.17) называется разложением определителя по элементам первой стоки.

Аналогичным образом можно получить разложения определителя по элементам других строк, а так же по элементам столбцов определителя.

Введем теперь понятие минора.

Минором данного элемента определителя п-го порядка называется определитель (п – 1)-го порядка, полученный из данного определителя вычеркиванием сроки и столбца, на пересечении которых стоит элемент.

Минор принято обозначать большой буквой с теми же индексами, что и у элемента. Например, в определителе 3-го порядка:

элементу соответствует ,

элементу соответствует .

Легко убедиться в том, что алгебраические дополнения и миноры связаны соотношением

. (1.18)

Это «правило определения знаков» для определителя 3-го порядка удобно представить следующей матрицей:

. (1.19)

Разложение определителя по элементам первой строки теперь можно записать следующим образом:

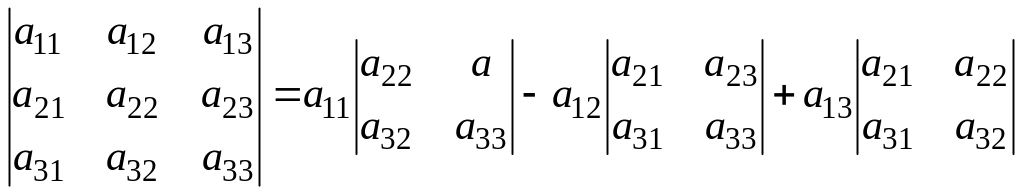. (1.20)

Аналогичным образом можно вычислить определитель, записывая его разложение по любой строке или столбцу.

Теперь можно сформулировать последнее свойство определителя.

Свойство 9. Сумма произведений элементов строки определителя на алгебраические дополнения этих элементов равна величине определителя.

Сумма произведений элементов строки определителя на алгебраические дополнения элементов другой строки равна нулю.

Докажем последнее утверждение на примере определителя 3-го порядка:

. (1.21)

Здесь в первой строке записаны произведения элементов второй строки определителя на алгебраические дополнения элементов первой строки. Это выражение равно определителю 3-го порядка, который равен нулю, как содержащий две одинаковые строки.

Утверждения свойства 9 справедливы и для столбцов.

Кроме того, на основе свойства 9 возможно вычисление определителя способом, который называется «разложением определителя по элементам строки или столбца».

1.6. Система трех линейных уравнений

Рассмотрим систему уравнений следующего вида:

(1.22)

где х, у и z – неизвестные, а_ij, h_i – заданные числа. Упорядоченная тройка чисел х₀, у₀, z₀ называется решением системы (1.22), если подстановка этих чисел в систему обращает все три уравнения в тождества. Теорема Крамера остается справедливой и для систем третьего и более высоких порядков (доказательство см. в пособии [1]).

Формулы Крамера для системы (1.22) приобретают вид,

(1.23)

где

.

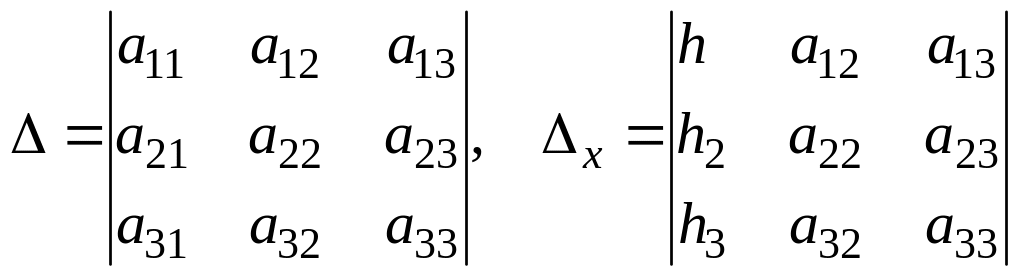
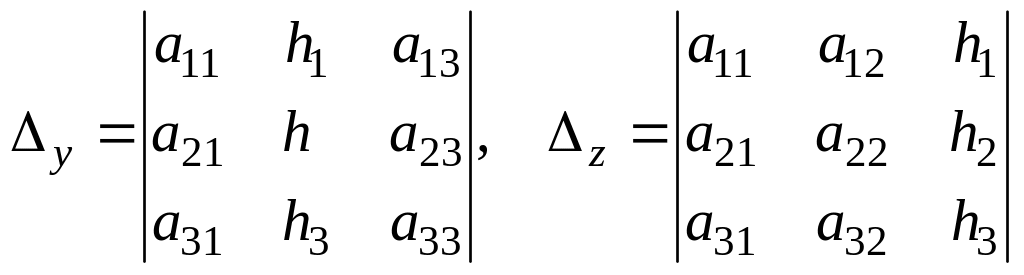Если определитель системы уравнений (1.22) , то существует единственное решение системы, определяемое формулами Крамера (1.23).

Проверка существования решения системы (1.22) осуществляется подстановкой полученных решений в уравнения системы.

Каждое из уравнений системы (1.22) является уравнением плоскости в пространстве, а три числа , являющиеся решением системы, суть координаты точки пересечения этих плоскостей.