2.3. Динамічне програмування

У всіх попередніх задачах лінійного чи нелінійного програмування економічний процес вважався статичним, тобто таким, що не залежить від часу. Тому оптимальний розв’язок заходився лише на один етап планування. Такі задачі отримали назву одноетапних або однокрокових.

У задачах динамічного програмування економічний процес залежить від часу (від кількох періодів (етапів) часу), тому знаходять ряд оптимальних розв’язків (для кожного етапу), що забезпечують оптимальний розвиток всього процесу в цілому. З цієї причини задачі динамічного програмування називають багатоетапними або багатокроковими.

Динамічне програмування є математичним апаратом, що дозволяє здійснювати оптимальне планування багатокрокових керованих процесів і процесів, що залежать від часу. Економічний процес називається керованим, якщо можна впливати на хід його розвитку. Керуванням (управлінням) називається сукупність рішень, які приймаються на кожному етапі для впливу на хід процесу.

Моделі математичного програмування (в загальному випадку) використовуються при дослідженні широкомасштабних проблем макроекономіки. У мікроекономіці вони ефективні, якщо розглядаються короткотермінові процеси, які можна вважати стабільними на досліджуваних проміжках часу. Моделі ж динамічного програмування використовують переважно при дослідженні задач мікроекономіки. На відміну від загальних задач математичного програмування вони дають можливість враховувати перебіг процесу в часі, оцінювати його стан, моделювати поетапне управління процесом.

У деяких випадках розбиття економічної операції на етапи відбувається природним шляхом. Наприклад, при плануванні господарської діяльності підприємства (чи групи підприємств) такими природними етапами є місяці, квартали, роки (що може бути пов’язане з необхідними термінами фінансової чи статистичної звітності тощо). В інших ситуаціях розбиття на етапи може носити штучний, умовний характер. Але особливістю усіх задач динамічного програмування є той факт, що на кожному етапі можна керувати перебігом досліджуваного процесу та оцінювати якість такого управління.

У плануванні багатоетапного процесу виходять з інтересів всього процесу в цілому, тобто, приймаючи рішення на окремому етапі, завжди потрібно мати на увазі кінцеву мету.

Нехай на m років планується діяльність заданої сукупності промислових підприємств, у розвиток яких планується вкласти певну кількість певних ресурсів. У процесі функціонування зазначеного промислового комплексу з k підприємств наявні ресурси витрачаються. Крім того, кожне підприємство щороку дає певний дохід, величина якого залежить від прийнятого розподілу ресурсів між підприємствами. На початку кожного господарського року можливий залишок ресурсів знову має бути перерозподілений між підприємствами.

Виникає запитання: як саме треба розподіляти наявні ресурси між підприємствами на початку кожного року, щоб загальний дохід від роботи цих підприємств впродовж наступних m років був максимальним?

Це є типова задача динамічного програмування. Наведемо її формалізований опис.

Нехай на початку і-того року j-тому підприємству (j = 1…k) виділено x_ij умовних одиниць певних ресурсів. Вектор з координатами характеризує прийнятий розподіл наявних ресурсів між всіма підприємствами у і-тому році.

Принцип оптимальності Беллмана. Розв’язок операції в цілому – це сукупність всіх покрокових розв’язків

, (2.3.1)

ефективність якого оцінюється за певним адитивним критерієм

, (2.3.2)

де Q_i – дохід всього комплексу підприємств наприкінці і-того року.

Отже, пропускаючи питання розподілу засобів між підприємствами на початку кожного господарського року, необхідно визначити розв’язок задачі Х*  R^mi такий, який максимізував би критерій (2.3.2).

Цю оптимізаційну задачу можна розв’язати різними способами: або шукати одразу розв’язок Х*, або будувати цей вектор поступово, крок за кроком, на кожному етапі розрахунків оптимізуючи лише результат даного кроку. Звичайно, що другий варіант розв’язування задачі є простішим за перший, особливо при великій кількості етапів.

Зазначена ідея поступової, покрокової оптимізації економічної операції складає сутність методу динамічного програмування.

На перший погляд, ідея достатньо проста! Якщо важко оптимізувати операцію в цілому – її розбивають на ряд кроків, кожен з яких стає окремою “маленькою операцією”, оптимізувати яку порівняно легко. Далі для кожного кроку вибирають рішення, при якому ефективність даного кроку буде максимальною. Однак це хибна інтерпретація! Визначаючи управління для кожного конкретного кроку, не можна забувати про інші кроки. Планування має враховувати перспективу. Який зміст максимізувати критерій даного етапу, якщо в подальшому це призведе до можливих втрат і завадить отримати максимальний дохід в цілому?

Розглянемо приклад динамічної задачі:

Нехай плановий період Т складається з n інтервалів (наприклад, років), і протягом цього періоду слід використати деякий ресурс В у кількості b. Можуть бути реалізовані два способи витрат ресурсу – І і ІІ. Відомо, що використання заданого ресурсу в кількості х першим способом дає прибуток g(x), а другим способом – h(x). Виникає задача оптимального розподілу ресурсу В на період Т для досягнення максимального прибутку.

Достатньо легко сформулювати однокрокову задачу для всього періоду Т:

максимізувати цільову функцію

(2.3.3)

при умовах

, (2.3.4)

. (2.3.5)

Якщо в цільовій функції (2.3.3) врахувати умову (2.3.4), то задача може бути записана у такому вигляді:

, (2.3.6)

. (2.3.7)

Тепер сформулюємо задачу оптимального поточного планування по інтервалах загального періоду, причому принцип планування полягатиме в перерозподілі тієї кількості ресурсу В між способами його використання, яка залишається на кінець j-того періоду. Критерій оптимальності не змінюється і полягає в максимізації прибутку за весь період часу Т.

Логічно припустити, що на кінець першого (початок другого) етапу залишиться деяка кількість ресурсу, яку можна описати виразом:

, (2.3.8)

де: c і d – коефіцієнти пропорційності, що характеризують

зміну кількості ресурсу відповідно при І та ІІ способі

його використання;

х₁ – кількість ресурсу, використаного на 1 етапі першим

способом;

b₁ – кількість ресурсу на початку 1 етапу.

Щоб розв’язати задачу досягнення максимального прибутку впродовж другого етапу, потрібно розв’язати задачу, аналогічну до задачі (2.3.6), тобто

, (2.3.9)

. (2.3.10)

Отже, для довільного k-того інтервалу можна записати:

(2.3.11)

при системі умов

(2.3.12)

Розв’язування задачі (2.3.11)-(2.3.12) розглянутими раніше одно кроковими методами може виявитися неможливим. Міркування, які привели до формулювання задачі (2.3.11)-(2.3.12), породжують ідею побудови алгоритму поетапного розв’язування задач такого типу.

Позначимо через F_n(b) максимальний прибуток, досягнутий внаслідок n-крокового процесу. Очевидно, що

, (2.3.13)

де всі змінні x_j підлягають обмеженням (2.3.12).

Якщо n = 1, то

. (2.3.14)

При n = 2 маємо

, (2.3.15)

де b₂ залежить від х₁:

Отже, при двокроковому процесі дослідженню на максимум підлягає функція

, (2.3.16)

а її максимум дорівнює

. (2.3.17)

Формула (2.3.17) є рекурентним співвідношенням, що пов’язує величину прибутку, досягнутого за другий інтервал періоду Т, з прибутком за обидва інтервали планового періоду.

Для загального прибутку, за аналогією, можна записати

, (2.3.18)

де значення F₁ визначається за формулою (2.3.14).

При плануванні багатокрокової операції необхідно на кожному її кроці приймати рішення з урахуванням його майбутніх наслідків на наступних кроках.

Звичайно, це правило має винятки. На останньому кроці будь-якої операції можна не враховувати майбутнє – після цього кроку наступних вже не буде. Цей крок єдиний можна планувати так, щоб він мав найбільший ефект. Маючи оптимальний розв’язок на останньому кроці, можна “добудовувати” до нього оптимальне управління передостаннього кроку, до нього – попереднього і т.д. Таким чином, процес динамічного програмування розгортається від кінця до початку: спершу планується останній, m-тий крок. Враховуючи, що при цьому невідомим є результат попереднього, (m – 1)-го кроку, потрібно робити різні припущення про те, чим закінчиться попередній крок, і для кожного з цих припущень щодо стану системи знайти такий розв’язок, при якому дохід на останньому кроці був би максимальним.

Отже, на кожному кроці відшукується таке управління, яке б забезпечило оптимальне продовження процесу відносно стану системи, досягнутого на даний момент. Цей принцип вибору управління називають принципом оптимальності Беллмана. Формулюється він так: при будь-якому стані системи, досягнутому за певну кількість кроків управління, на наступному кроці управління потрібно вибирати так, щоб воно разом з оптимальним управлінням для всіх наступних кроків, необхідних для закінчення процесу, починаючи з даного кроку, забезпечувало оптимальний результат завершення всього процесу в цілому.

Принцип оптимальності стверджує, що для будь-якого процесу без зворотного зв’язку оптимальне управління системою в цілому містить в собі оптимальне управління для будь-якого частинного процесу (на проміжному етапі) стосовно його вихідного стану.

До найтиповіших задач динамічного програмування належать задачі такого економічного змісту:

а) задачі управління запасами (коли потрібно визначити час та обсяг поповнення продукції);

б) моделі календарного планування (які дають змогу спланувати роботу об’єкта з максимальною ефективністю на даному проміжку часу);

в) задачі визначення необхідного обсягу запасних частин (для гарантування ефективної роботи обладнання);

г) задачі перспективного планування;

а також цілий ряд інших задач.

Зробимо наголос на особливостях моделювання задач у динамічному програмуванні:

• задача оптимізації може бути розв’язані за N керованих кроків;

• цільова функція є адитивною на кожному кроці можливого управління, тобто вона дорівнює сумі значень цільових функцій на кожному кроці процесу;

• вибір управління на кожному кроці залежить лише від досягнутого на попередньому етапі стану системи і не впливає на її стан за попередні кроки (відсутній зворотний зв’язок);

• стан S_i системи після і-того кроку управління залежить тільки від попереднього стану S_i-1 та управління U_i (відсутність післядії);

• на кожному кроці як управління U_i, так і стан S_i системи залежать лише від скінченої множини параметрів.

Геометрична інтерпретація задачі. Стан довільної системи S можна описати деякими числовими параметрами. Назвемо такі параметри координатами системи. Тоді стан системи можна зобразити точкою S, а перехід зі стану S₁ у стан S₂ – траєкторією руху точки S. Управління U означатиме вибір певної траєкторії руху точки, тобто встановлення певного закону руху.

Сукупність можливих станів, в які може переходити система, називається областю можливих станів. Залежно від числа параметрів, що характеризують стан системи, область можливих станів системи буде різною (інтервал на числовій осі, частина площини, деякий об’єм тощо).

Отже, задачі динамічного програмування можна надати таку геометричну інтерпретацію: зі всіх траєкторій, що належать області можливих станів системи і з’єднують початковий і кінцевий стан, потрібно вибрати таку, на якій критерій W зміни стану системи набуває оптимального значення.

Основні типи графічних задач динамічного програмування. Розглянемо кілька типових задач динамічного програмування, які розв’язуються при допомозі графічного методу.

Задача про мінімізацію витрати пального. Нехай пілот літака, що знаходиться на висоті Н₀ зі швидкістю V₀, має завдання підняти літак на висоту Н_к, набравши швидкість V_к. Відома витрата пального при підйомі літака з довільної висоти Н₁ на висоту Н₂ > Н₁ при постійній швидкості, а також витрата пального при збільшенні швидкості від довільного значення V₁ до V₂ > V₁ при незмінній висоті. Необхідно знайти оптимальне управління набором висоти і швидкості, при якому витрата пального була б мінімальною.

З умови видно, що стан системи S (літака) характеризується двома параметрами: швидкістю V і висотою Н. Тому розв’язок будемо шукати на площині VOH, а, точніше, на прямокутнику, обмеженому прямими V = V₀, V = V_к, Н = Н₀ і Н = Н_к. Цей прямокутник і є областю допустимих станів. Початковий S₀ і кінцевий S_к стани визначені точками на площині (рис.2.1).

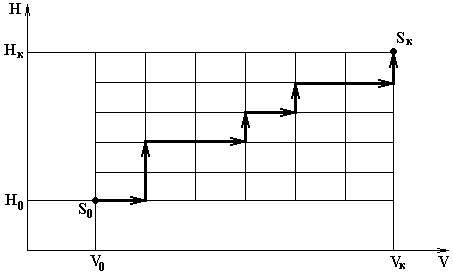
Рис.2.1.

Для побудови розв’язку методом динамічного програмування розбивають відрізки (Н_к – Н₀) і (V_к – V₀) на n₁ i n₂ рівних частин (етапів) відповідно і домовляються, що за один етап (крок) літак може або збільшити висоту на або швидкість на . Очевидно, що існує багато траєкторій, які будуть ламаними лініями, що з’єднуватимуть точки S₀ і S_к. Розв’язок задачі полягає в тому, щоб мінімізувати витрати пального, які будуть сумою витрат пального на кожному кроці, тобто визначити траєкторію, при русі якою витрати пального будуть мінімальними.

Задача визначення найкоротших віддалей по заданій мережі. Ця задача знайшла широке застосування для визначення величин вартості C_ij, що входять у критерій оптимальності при розв’язуванні транспортної задачі лінійного програмування. Розв’язок задачі з визначення найкоротших віддалей між постачальниками і споживачами по існуючій транспортній мережі є вихідним етапом при розв’язуванні таких економічних задач як оптимальне закріплення споживачів за постачальниками, підвищення продуктивності транспорту за рахунок зменшення непродуктивного пробігу тощо.

Нехай на деякій поверхні є скінчене число точок Р_n, з’єднаних між собою можливими відрізками ліній (Р_iР_j), що не перетинаються. Ці відрізки називаються ланками або зв’язками. Тоді сукупність точок та їх зв’язків називатиметься мережею.

Мережа називається достатньо зв’язаною, якщо існує шлях, що складається з ланок і з’єднує будь-які дві точки мережі. У задачі необхідно визначити найкоротші віддалі по мережі від кожної точки до решти точок і відповідні шляхи, по яких вони проходять.

На конкретному прикладі розглянемо алгоритм розв’язування такої задачі.

Приклад. Нехай задана достатньо зв’язана мережа, на якій кожній ланці поставлене у відповідність деяке невід’ємне число – довжина. Необхідно визначити найкоротші віддалі від усіх точок мережі до точки 8 та відповідні маршрути (рис.2.2).

Задачу розв’язують так. Записуємо біля кружечка точки 8 нуль. Визначимо характеристики точок 4, 6 і 7, сусідніх до неї, і стрілками біля кожної точки вкажемо напрям найкоротшої ланки. Точку 8 позначимо значком .

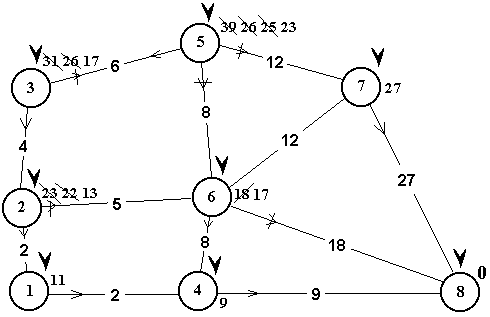
Рис.2.2.

Розглянемо точку 7. Визначимо характеристики точок 5, 6 і 8, сусідніх з нею. Характеристику точки 5, рівну 39, запишемо біля неї, вказавши стрілкою напрям. Для точок 6 і 8 нові характеристики відповідно рівні 39 > 18 і 54 > 0. Отже, визначені раніше для них характеристики залишаємо без змін. Точку 7 відзначаємо знаком .

Розглянемо точку 6. Сусідніми до неї є точки 2, 4, 5, 7 і 8. Характеристику точки 2, рівну 23, запишемо біля неї і вкажемо напрям. Для точки 4 нова характеристика 26 > 9 (зміни не вносимо), для точки 5 характеристика 26 < 39. Тому запишемо нову характеристику і замінимо напрям найкоротшого зв’язку. Для точок 7 і 8 нові характеристики відповідно 30 > 27 і 36 > 0, тому залишаємо все без змін. Точку 6 відзначаємо знаком .

Розглянемо точку 4 та її сусідні точки 1, 6 і 8. Характеристику точки 1, рівну 11, запишемо біля неї і вкажемо напрям. Для точки 6 нова характеристика 17 < 18. Змінюємо характеристику й напрям для точки 6. Оскільки точка 6 відзначена знаком , перераховуємо характеристики точок 2, 5, 7, 8, сусідніх з нею, і при необхідності змінюємо напрям. Для точки 2 нова характеристика 22 < 23, отже, змінюємо характеристику; для точки 5 характеристика 25 < 26 – міняємо характеристику на нову, для точок 7 і 8 відповідно 29 > 27, 35 > 0. Відзначаємо точку 4 знаком .

Розглянемо точку 5 і сусідні точки 3, 6 і 7. Характеристику точки 3, рівну 31, запишемо поряд з нею і вкажемо напрям. Характеристики точок 6 і 7 залишаються без змін. Точку 5 відзначаємо .

Характеристики точки 3 і сусідніх точок 2 і 5 не змінюємо і відзначаємо точку 3 знаком .

Розглянемо точку 2 і сусідні точки 1, 3 і 6. Характеристики точок 1 і 6 не змінюються. Для точки 3 нова характеристика 26 < 31, отже, міняємо характеристику і напрям. Оскільки точку 3 відзначено, перераховуємо характеристику точки 5. Вона не змінюється.

Відзначаємо точку 2.

Розглянемо точку 1 та сусідні точки 2 і 4. Для точки 2 нова характеристика 13 < 22 – міняємо характеристику і напрям. Точка 2 має позначку, тому перераховуємо характеристики для точок 3 і 6. Для точки 3 нова характеристика 17 < 26 – змінюємо характеристику і перераховуємо параметри для точки 5. Для неї 23 < 25 – змінюємо характеристику, напрям і перераховуємо дані для точок 6 і 7. Для них все залишається без змін. Характеристики для точки 6 залишаються без змін і при перерахунку з боку точки 2. Для точки 4 характеристика не міняється. Точку 1 відзначаємо знаком .

Всі точки відзначені, тому розв’язок задачі закінчений. Оптимальний розв’язок заносять у відповідну таблицю (табл.2.1).

Таблиця 2.1

№№ точок	Найкоротша віддаль	Маршрут
1 – 8	11	1 – 4 – 8
2 – 8	13	2 –1 – 4 – 8
3 – 8	17	3 – 2 –1 – 4 – 8
4 – 8	9	4 – 8
5 – 8	23	5 – 3 – 2 –1 – 4 – 8
6 – 8	17	6 – 4 – 8
7 – 8	27	7 – 8
8 – 8	0	8

У загальному випадку при розв’язуванні подібних задач знаходять можливі найкоротші віддалі між кожною парою точок мережі і будують подібні таблиці. Це дає змогу визначати оптимальний маршрут між будь-якими двома точками мережі.

У вигляді мереж можна зобразити багато типів задач. Наприклад, звичайна транспортна задача може бути представлена у мережному вигляді (рис.2.3).

Д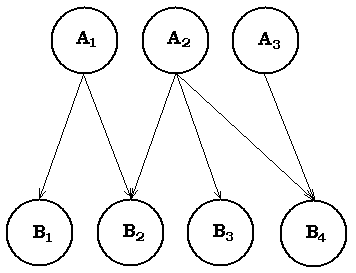 ля забезпечення повноти даних на схемі необхідно над відповідними стрілками, що з’єднують постачальників і споживачів, записувати питомі вартості перевезень, і потім у спеціальній таблиці вказати обсяги перевезень, які забезпечуватимуть оптимальний план перевезень.

Рис.2.3.