§2. Изопериметрические задачи.

Задача Дидоны является частным случаем так называемых изопериметрических задач. Это название происходит от двух греческих слов isos – равный и perimetron – обмер, обвод. Изопериметрическая задача состоит в том, чтобы среди данной совокупности фигур, имеющих одинаковую длину контура (одинаковый периметр), найти ту, чья площадь больше площади любой другой фигуры рассматриваемой совокупности.

Рассмотрим два простых примера. Пусть выделенный класс геометрических фигур состоит из всех треугольников с данным периметром L, у которого площадь максимальна. Таким треугольником является равносторонний ( со стороной L/3). Если в качестве выделенного класса взять множество всех прямоугольников с фиксированным периметром, то решение соответствующей изопериметрической задачи будет квадрат. О чем мы убедились в §1.

Значительно более сложной является

Основная изопериметрическая задача.

Среди всех плоских фигур данного периметра L найдите ту, которая имеет максимальную площадь.

Ответ, конечно – круг. Еще в др. Греции было известно, что круг имеет большую площадь, чем все другие фигуры с тем же самым периметром, а шар – наибольший объем среди всех тел с одной и той же поверхностью.

Хотя ответ в основной изопериметрической задаче очевиден, про доказательство это сказать нельзя. Только Л.Эйлеру в 18 веке удалось доказать изопериметрическое свойство круга с помощью вариационного исчисления, т.е. нового раздела высшей математики, которую он создал. Попытка привести элементарное доказательство принадлежит швейцарскому математику Я.Штейнеру (1796-1863).

Учитывая вышеприведенные понятия, для треугольников можно сформулировать следующие утверждения.

1.Среди треугольников, вписанных в данный круг, наибольшую площадь (и периметр) имеет правильный треугольник.

2.Среди треугольников, описанных около данного круга, наименьшую площадь (и периметр) имеет правильный.

3.Среди треугольников данного периметра наибольшую площадь имеет правильный.

4.Среди треугольников с данной минимальной высотой наименьшую площадь (и периметр) имеет правильный.

5.Среди треугольников с данной максимальной стороной наибольшую площадь (и периметр) имеет правильный.

Далее аналоги утверждений 1-5 будут доказаны для произвольных выпуклых n-угольников.

Отметим, что если радиус круга, длина которого l, равен r=l/2, то максимальная площадь равно r²=(l/2)²=l²/4. Таким образом, если S – площадь какой–нибудь фигуры с периметром l, то S l²/4.

Это неравенство называется изопериметрическим неравенством.

Если Дидона не использовала берег моря, то максимальная площадь, которая она могла бы оградить шнуром длины l, была бы l²/4.

§3. О попытке решения Штейнера основной изопериметрической задачи.

Рассматриваются всевозможные фигуры на плоскости с данным периметром p. Установим сперва некоторые свойства максимальных (по площади) фигур этого класса.

Первое свойство. Всякая максимальная фигура выпукла, то есть любая хорда, соединяющая две ее точки, целиком в ней лежит.

Второе свойство. Всякая хорда максимальной фигуры с периметром р, делящая пополам ее периметр, обязательно делит ровно пополам и ее площадь.

Третье свойство. Всякий диаметр любой максимальной фигуры виден из всех точек ее контура под прямым углом (по есть для любого диаметра AC и любой точки B контура угол AВC равен 90⁰).

Все свойства мы привели без доказательства. Их можно доказать. Например, для док-ва третьего свойства используется лемма 1,§1.

Из третьего свойства сразу следует, что искомая максимальная фигура является кругом: Действительно, выберем произвольный диаметр; тогда контур фигуры, по третьему свойству, состоит из вершин прямых углов, опирающихся на этот диаметр, то есть является окружностью. Что и требовалось доказать.

B

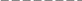A C

Рассуждение Штейнера, как может показаться на первый взгляд, завершает доказательство основной теоремы об изопериметрах, где мы с самого начала предположили, что решение основной изопериметрической задачи существует.

Это незаконное предположение, поскольку существование решения надо доказать. Такое доказательство выходит за рамки элементарной математики (с помощью вариационного исчисления).

I. Неравенства для площади и периметра выпуклого многоугольника.