Лабораторна робота № 12

ВИВЧЕННЯ МЕТОДУ МІНІМАКСА

Мета роботи: вивчення методу мінімакса для діагностування технічного стану досліджуваних систем і об’єктів.

Завдання заняття: розрахувати за методом мінімакса граничний стан діагностичного параметра, вище якого досліджуваний об’єкт підлягає зніманню з експлуатації.

Тривалість: 2 год.

ОСНОВНІ ТЕОРЕТИЧНІ ПОЛОЖЕННЯ

Загальні відомості. Метод мінімакса призначений для ситуацій, коли відсутні попередні статистичні дані про ймовірності діагнозів D₁ і D₂. Розглядається «найгірший випадок», тобто найменш сприятливі значення P₁ і P₂, що призводять до найбільшого значення (максимуму) ризику.

Будемо вважати, що величина ризику залежить тепер від х₀ і Р₁ (ймовірність другого діагнозу Р₂=1-Р₁). Із співвідношення випливає, що

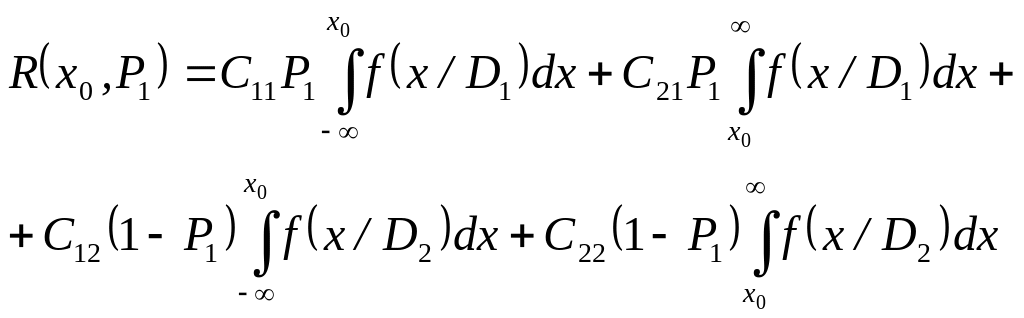(12.1)

Для знаходження екстремума прирівняємо до нуля часткові похідні по х₀ і Р₁. Умова

(12.2)

дає

(12.3)

Із співвідношення

(12.4)

отримуємо:

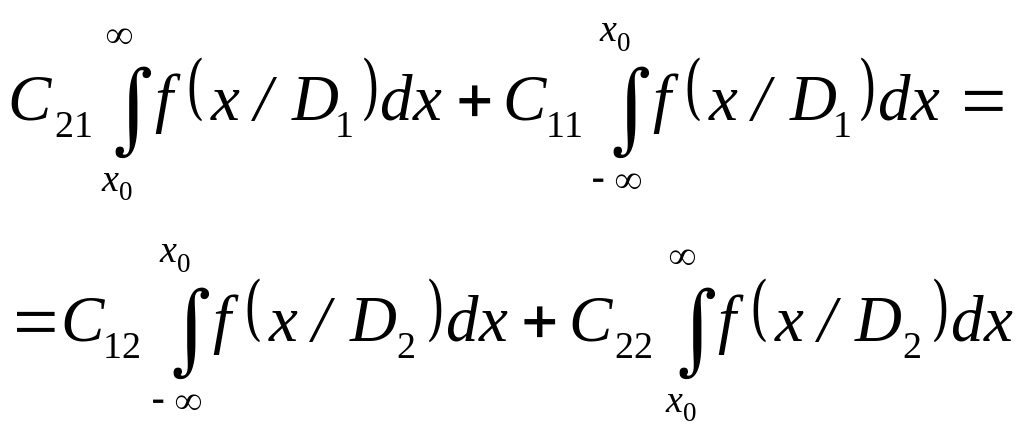(12.5)

Тепер необхідно визначити значення х₀ і Р₁, що задовольняють рівнянням (12.3) і (12.5). Якщо і є коренями зазначених рівнянь, то точка ) являється екстремальною.

Можна показати для одномодальних розподілів, що величина ризику стає мінімаксною (тобто мінімальною серед максимальних значень, викликаних “несприятливою” величиною Р₁). Відмітимо, що за Р₁=0 і Р₂=1 ризик прийняття помилкового рішення відсутній, оскільки ситуація не має невизначеності. За Р₁=0 (всі вироби несправні) із умови (13.4) випливає і всі об’єкти дійсно признаються несправними; за Р₁=1 і Р₂=0 і відповідно до наявної ситуації всі об’єкти класифікуються як справні.

Для проміжних значень 0<P1<1 ризик зростає і при стає максимальним. Розглянутим методом вибирають значення х₀ таким чином, щоб за найменш сприятливих значень P₁ втрати, пов’язані з помилковими рішеннями, були б мінімальними.

Розглянемо процедуру розв’язку рівнянь (12.3) і (12.5). Спочатку з рівняння (12.5) знайдемо значення , що можна зробити наступним чином. Представимо рівняння (12.5) у вигляді

(12.6)

де

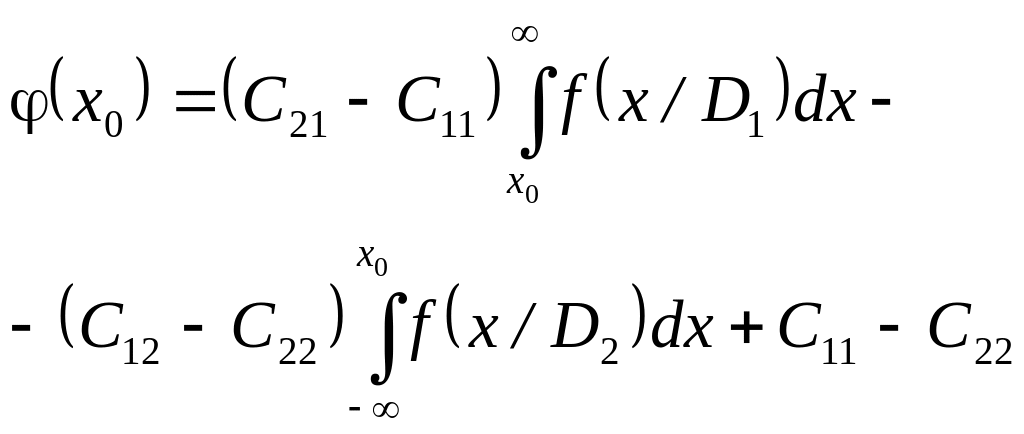(12.7)

Останнє рівняння можна записати з допомогою функції розподілу

, (12.8)

Рівняння (12.6) вирішуємо за методом Ньютона, який пов’язує вихідні х_0(n-1) і наступні х_0(n) наближення:

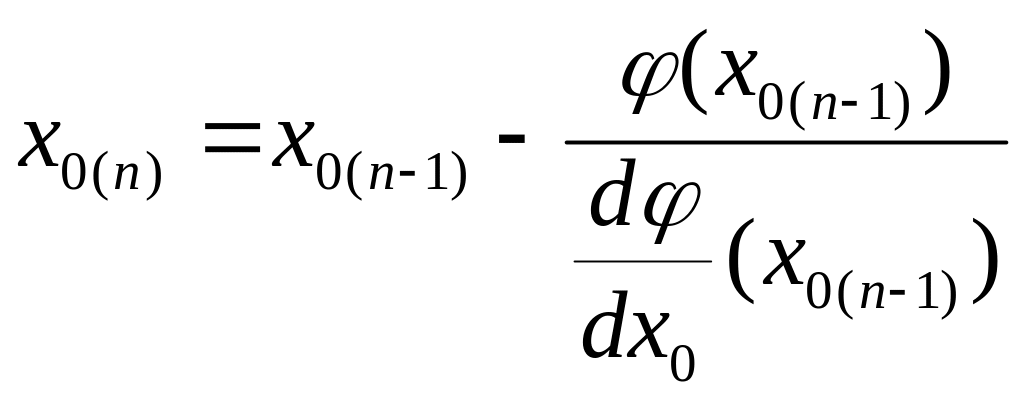(12.9)

Значення похідної:

(13.10)

В якості першого наближення можна прийняти _, де , - середні значення х для розподілів і . За достатньої близькості х_0(n) і х_0(n-1) приймаємо . Далі із рівняння (12.3) знаходимо найменше сприятливе значення ймовірностей справного і несправного станів:

, (12.11)

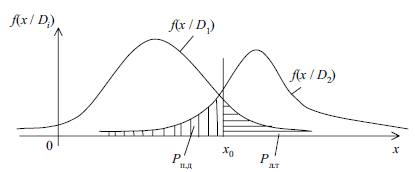
Рисунок 12.1 – Визначення граничного значення діагностичного параметру за методом мінімаксу

Величину ризику визначаємо за рівнянням (12.1) при значеннях , . Відмітимо деякі випадки, у яких розв’язок стає достатньо наглядним. Припустимо, що умовні виграші відсутні , а ціни помилок однакові . Тоді з рівняння (12.5) випливає:

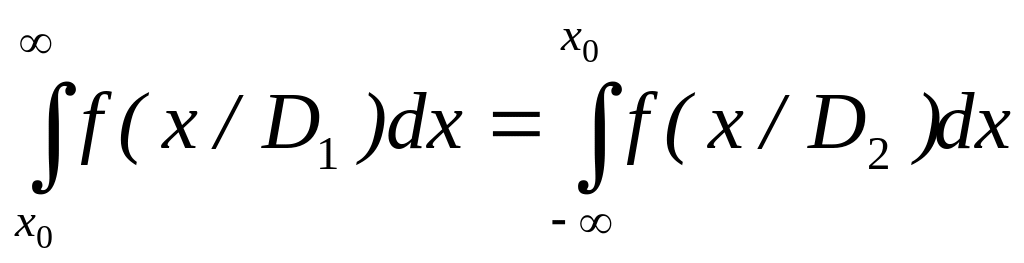
або

,

де і - відповідні функції розподілу. Останні відношення показують рівність умовних ймовірностей помилкових рішень.

На рис.12.1 для цього випадку і рівні. У загальному випадку

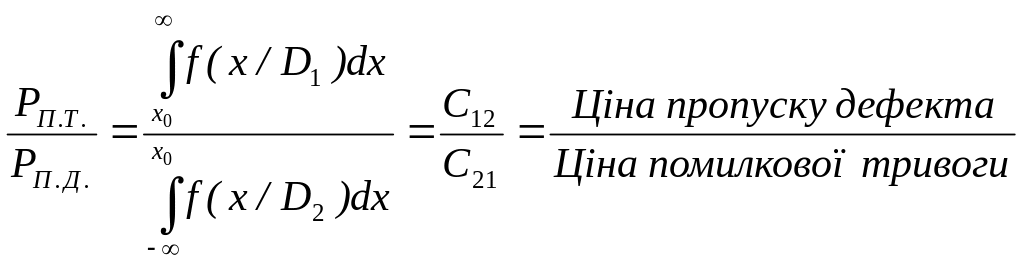
(12.12)

Залежність (12.12) виражає рівність умовних ризиків помилкових рішень. За допомогою функції розподілу вона записується у вигляді:

(12.13)

Приклад. Діагностування стану трансмісії газотурбінного двигуна здійснюється за вмістом заліза у маслі. Для справного стану середнє значення складає (5 г заліза на 1 т масла) і середньоквадратичне відхилення . За наявності дефекту підшипників та інших деталей (несправний стан) ці значення рівні . Розподіли вважаються нормальними.

Необхідно визначити граничний вміст заліза у маслі, вище якого двигун підлягає зніманню з експлуатування і розбиранню (щоб уникнути небезпечних наслідків). За статистичним даними несправний стан трансмісії спостерігається у 10% двигунів.

Граничне значення х₀ розраховується за рівнянням (12.8)

Для нормального розподілу функції розподілу виражаються з допомогою функцій Лапласа:

де

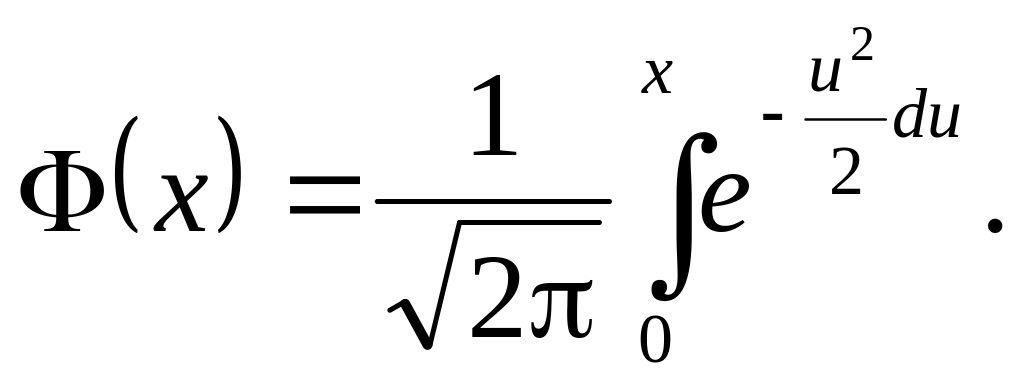
Розрахунок проводиться за формулою (12.9). Перше наближення:

Друге наближення:

Значення . Розрахунки дають . При розрахунку використовувались таблиці для нормального розподілу (додаток Б). Наступні наближення дали При отримано Значення найбільш несприятливих ймовірностей станів при

При