Тема7. Выборочный метод. Расчёт средней, предельной ошибки выборки. Расчёт оптимальной численности выборки.

1. Теоретическая база.

Для выполнения данной работы студент должен владеть лекционным материалом по данной теме, а также должен быть знаком со специальной литературой по данному вопросу, особенной 124-154.

2. Основы теории по данной теме. Определение, терминология.

Выборочный метод статистического наблюдения (СН) - это метод изучения социально-экономических явлений и процессов, при котором основные характеристики совокупности определяются на основе изучения какой-то ее части, базируясь на методах случайного отбора. Обычно обследуется 5-10 % единиц изучаемой совокупности, реже 15-25 %(стр. 124)

При этом различают понятия генеральной совокупности и выборочной совокупности (выборки). Генеральная совокупность ~ это совокупность экономических явлений, которая подлежит изучению.

Выборочная совокупность (выборка) - это часть, единиц генеральной совокупности, которая подвергается сплошному изучению.

Между характеристиками выборки и генеральной совокупности объективно имеются расхождения, которые называются ошибкой выборки. Поэтому основной задачей выборочного наблюдения является минимизация ошибки выборки.

В выборочном методе исследования социально-экономических явлений используются в основном следующие показатели:

а)Средняя величина альтернативного количественного признака "X";

б)Относительная величина альтернативного признака " w ".

Средняя величина количественного признака - это усреднённое значение варианты (X) в ряду распределения, которым представлены изучаемые данные. Для генеральной совокупности обозначает-

_ _

ся как X , для выборки - как X .

Относительная величина альтернативного признака - это удельный вес (в % или коэффициентах) в общей совокупности единиц наблюдения, обладающих изучаемым признаком. Для генеральной совокупности - обозначается как "Р", для выборки - как " W". Эту величину в статистике называют ещё "частостью".

Методический алгоритм применения выборочного метода сбора данных об изучаемой социально-экономической совокупности поясним на следующем примере.

Исходные данные:

при анализе уровня доходов населения районного центра М было проведено 5% выборочное обследование населения бесповторным методом, механическим способом. При этом в выборку попало 250 человек, для которых удельный вес населения с годовым доходом 500 рублей составил 200 человек. Средний годовой доход в выборке составил 5000 рублей при среднем квадратическом отклонении σ = ±2000 рублей.

Требуется: _

1. На основе исходных данных определить значение X и Р для генеральной совокупности. _

2. Определить значение средней ошибки выборки для X и Р.

3. Определить достоверность значений ошибки выборки с вероятностью 0,9545.

4. Определить предельную ошибку выборки с учётом коэффициента доверия по указанной вероятности.

Алгоритм решения задачи:

m

1 .Определим "W" как W = ---- (7.1)

n

m - количество единиц совокупности населения, которое имеет годовой доход < 5000 рублей.

N - количество населения в выборке.

Тогда 200

W = ------- = 0.8

250

Средний доход 5000 рублей определен по формуле

n

∑ Xi * fi

_ i = 1

X = -------------------- (7.2)

n

∑ fi

i=1

где: Xi - варианта; f - частота распределения

2. Определяется средняя ошибка выборки (М)

σo²

   ----- (7,3)

n

В формуле (7.3) величина σo² - генеральная дисперсия. Определение её значения составляет суть выборочного метода. Между дисперсиями генеральной и выборочной совокупности существует следующее соотношение

n

σo² = σ² * -------

n – 1 (7,4)

n

т.е. σ² < σo² в -------- раз, где σ² дисперсия выработки

n – 1

_

∑(Xi – X)² * f

σ² = ------------------

∑ f

_{ } (7.5) или

σ² = X² - (X)² (7,6)

n

Если n достаточно велико, то отношение -------- близко к единице, т. е. n - 1

σx² = σ² (7.7)

В этом случае значение средней ошибки выборки по формуле

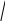
σ²

  ----- (7,8)

 n

При этом для доли альтернативного признака дисперсия в выборочной совокупности определяется:

σx²=w*(l-w) (7.9)

Для показателя средней величины количественного признака в выборке может

_

∑(Xi – X)

быть определена по формуле : σx² = ------------ (7.10) либо по формулам (7.5) и (7.6) n

Надо иметь в виду, что формула (7.8) используется только при повторном отборе (каждая изучаемая единица наблюдения после фиксации снова возвращается в генеральную совокупность), но повторный отбор используется крайней редко. Для бесповоротного отбора в формулу (7.8) включается дополнительный множитель

n

1- ---, где n - количество единиц в выборке.

N

N - количество единиц в генеральной совокупности.

Тогда формула средней ошибки выборки принимает следующий вид :

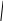
σ² n

w  ----- (1 - --- ) (7,11)

 n N

Для нашего случая определим значение средней ошибки выборки : а) для показателя W

w*(1-w) n 0.8(1-0.8) 250

w  -------- (1 - ---) = ------------ (1 - ------ ) = ±0.025 (7.12)

 n N  250 5000

_

б) для показателя среднего дохода X

σx² n 200² 250

x  ----- (1 - ---) = ------------ (1 - ------ ) = ±12.3 (7.13)

 n N  250 5000

(значение 200² из условия задачи)

Полученные в результате расчётов (7.12), (7.13) значения «W» и

_

«X» будут использованы для установления возможных значений «Р» и «X ».

Одно из возможных значений «Р» определяется по формуле

P = W ± w (7.14),

т. е. Р = 0.8 ±0.025

_

Одно из возможных значений «X » определяется по формуле

_ _

X = X ± w (7.15),

_

т. е. X = 5000p ± 12,3руб.

_

Таким образом, характеристики «Р» и « X » отличаются от «W» и

_

«X» на величины средней ошибки выборки ±  .

_

Причём доказано, что пределы «Р» и « X » отличаются от «W» и

_

«X» на величину ±  лишь с вероятностью 0,683.

Вероятность суждения можно повысить, если увеличить  в t раз. Тогда при t=2 вероятность суждения достигает 0,954 при t=3-0.9973 и т. д.

В этом случае

P = W + t *w (7.16)

_ _

X = X + t*x (7.17)

Множитель t называется коэффициентом доверия. Конкретные значения множителя t для различных степеней вероятности определяется по функции Ляпунова А. М.

1 +1 -1²

F (t) = ---------  e ² * dt (7.18)

 2* _-1

На практике пользуются готовыми таблицами, которые вычислены для различных значений t по нормальным распределениям. Выписка из таблицы.

Кратность ошибки t	Вероятность f(t)	Кратность ошибки t	Вероятность f(t)
0,0	0,0000	2,0	0,9545
0,1	0,0797	2,5	0,9876
0,5	0,3829	2,6	0,9907
1,0	0,6827	3,0	0,9973
1,5	0,8664	4,0	0,999937

В нашем случае по условию задачи мы должны рассчитать среднюю ошибку выборки с вероятностью суждения 0,9545. По таблице этому значению вероятности соответствует коэффициент доверия t = 2,0.

Тогда:

Р = 0.8±2-0.025

_

X= 5000±2-12.3 руб.

Это и будет ответом на 3 вопрос задачи. В практике выборочных наблюдений также используется показатель - предельная ошибка выборки (Δ).

Δ = t -  (7.19).

Если в формулу (7.19) подставить конкретные  при бесповторном отборе, то предельную ошибку можно записать следующим образом:

а) Для

w * (1 – w) n

ΔX = t --------------- * 1 - ---- (7.20)

 n N

б) для X

˜ σx² n

ΔX = t ------ * 1 - ----

 n N

Тогда для нашего случая предельная ошибка доли альтернативного признака Aw=2 (±0,025)= ±0,05т.е. ±5% Ах = 2(± 12,3 р) = ±24,6руб

Расчёт оптимальной численности выборки.

При использовании выборочного метода сбора информации об объекте наблюдения следует иметь ввиду, что размер ошибки выборки зависит, прежде всего, от численности выборочной совокупности, т.е. чем больше численность выборки, тем меньше средняя ошибка выборки . Здесь есть следующая закономерность - средняя ошибка выборки обратно пропорциональна п , т.е. при увеличении n в 4 раза её ошибки уменьшаются в 4 в 2 раза. Таким образом, увеличивая п можно довести ошибку выборки до сколь угодно малых значений. Проблема заключается в том, что при увеличении п растут затраты на проведение исследования, а при большом уменьшении п увеличиваются средние и предельные ошибки выборки. Поэтому необходимо определить оптимальную численность выборки.

Проведя определенные преобразования формулы предельной ошибки выборки:

_

а) для X:
σx² Если ΔX = t ----- (7.21)  n
- для min n
σx² - и ΔX² = t² * ----- (7.22) n
t² * σx² - отсюда nx = ---------- (7.23) ΔX²
б) для W: Δw² = t² * w(1-w)
t² * w(1-w) тогда nw = -------------- (7.34) Δw²
При бесповоротном отборе: Nt² * w(1-w) а) для nw = --------------------------- (7.25) N * Δw² + t² * w(1-w)
Nt² * σ² б) для nx = ---------------------- (7.26) N * Δx² + t² * σx²

Пример: исходя из целей исследования дохода населения, необходимо определить оптимальный объем. выборки из численного населения 5000 человек, чтобы с вероятностью 0,997 предельная ошибка среднегодового дохода не превысила 3%.

Решение :

5000 *(±3)

ΔX = ---------- = ±150руб.

100

5000 * 3² * 2000²

Подставляя в формулу (7.26) получаем п_x = ------------------------- =

5000*150²+3² * 2000

= 140человек

3. Задачи для самостоятельного решения

Задача 1. При контрольной проверке 1000 катушек медного провода, поставленного по договору, было проведено 5% выборочное обследование. При этом из 50 попавших в выборку (случайная бесповторная выборка) 40 штук соответствовало требованиям стандарта по техническим характеристикам провода. Средняя длина провода в выборке в среднем ее ставила 99м при среднем квадратическом отклонении (σ) = ±2м

Требуется определить возможные значения удельного веса(доли) стандартных катушек и средней длины намотки провода для всей партии катушек с вероятностью f(t)=0,987, с учётом предельной ошибки выборки.

Задача 2. В адрес базы МТС СМУ поступило от поставщика согласно договора о поставке 60 т. труб для электромонтажных работ. При контрольной проверке проведена механическая 5% выборка по бесповторному способу. При этом из 75 штук попавших в выборку труб соответствовало требованиям стандарта 65 штук. Средняя длина одной трубы в выборке 4,9 м при среднем квадратическом отклонении (σ) = ± 0,15 м. Требуется с вероятностью 0,997 определить пределы значений доли стандартных труб и средней длины трубы во всей партии поставки с учетом предельной ошибки репрезентативности.

Задача 3. На оптовую базу торговой фирмы поступило по договору 20.000 250-граммовых банок рыбных консервов конкретного наименования. Для контроля качества поставленной продукции проведена 5% случайная бесповторная выборка. При обследовании выборочной партии получены следующие данные:

1. Доля стандартных банок по содержанию составляет 65%.

2. Средний вес одной банки 248 г при среднем квадратическом отклонении (σ) = ± 6 грамм.

Требуется с вероятностью 0,987 определить возможные пределы изменения значений доли стандартных банок и их среднего веса во всей партии поставки с учетом предельной ошибки репрезентативности.

Задача 4. Исходя из требований стандарта требуется определить оптимальный объем выборки партии стирального порошка в количестве 5.000 коробок, чтобы с вероятностью 0,997 предельная ошибка выборки не превысила 5% веса 400 граммовой коробки.

Задача 5. Исходя из требований ТУ по качеству продукции фирмы, требуется определить оптимальный объем выборки партии автомобильных сальников 10.000 штук, чтобы с вероятностью 0,999 предельная ошибка выборки не превышала 0,05% установленную долю стандартных изделий 0,95 по условиям поставки.

Задача 6. При контроле качества электрических ламп накаливания проводится 5% обследование соответствия электрических ламп стандарту. Из 2.5 тысяч ламп попавших в механическую бесповторную выборку требованиям ГОСТа соответствовало 98% при среднем квадратическом отклонении ± 1,2%.Требуется с вероятностью 0,945 определить долю стандартных ламп во всей партии.

Задача 7. При исследовании среднего годового дохода населения района № проведено 5% бесповторное случайное выборочное исследование. Из 500 человек, попавших в выборку, средний годовой доход составил 5.400 рублей при среднем квадратическом отклонении (σ) = ±2,5. Требуется определить с вероятностью 0,954 средний доход жителей района.