
- •Общие понятия теории моделирования
- •Цели моделирования
- •Общая классификация моделей
- •Классификация идеальных моделей
- •Логико-математические модели
- •Компьютерные модели
- •Модель динамико-биологических популяций
- •Математическое моделирование химических процессов
- •Незатухающие колебательные процессы в химии
- •Затухающие колебания в химических процессах
- •Моделирование движения маятника
- •Вводная к лабораторной работе №1
- •Качественная теория динамических систем
- •Тримолекулярная модель (брюсселлятор)
- •Не существует
Качественная теория динамических систем
Качественная теория динамических систем предполагает, что исходная система дифференциальных уравнений (второго порядка) уже линеаризована в окрестности одной из своих особых точек.
Предположим, мы нашли особую точку для какой-либо и системы и линеаризовали систему в окрестности этой точки. Наша линеаризованная система имеет вид:
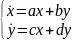
Представим систему в матричном виде: слева столбец производных, а справа – столбец свободных членов
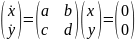
Делаем
вывод, что данная система всегда имеет
тривиальное решение
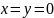 .
Система будет иметь нетривиальное
решение, если определитель матрицы
будет равен нулю, т. е. когда
.
Система будет иметь нетривиальное
решение, если определитель матрицы
будет равен нулю, т. е. когда
 .
.
Составим
для исходной системы характеристическое
уравнение
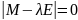 .
Распишем это уравнение:
.
Распишем это уравнение:
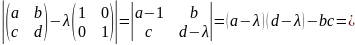
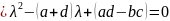
Найдём
корни
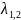 этого характеристического уравнения:
этого характеристического уравнения:

Новый
термин: трек – это сумма элементов
главной диагонали, обозначение –
 .
.
Тип особых точек исследуемой линеаризованной системы определяется корнями характеристического уравнения.
Выполнить отчёты по всем лабораторным работам с обложкой “Контрольная работа” |
26.04.2012 Лекция |
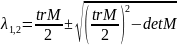
Опишем всевозможные результаты корней:
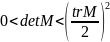 =>
корни
вещественные, неотрицательные и
различные, а фазовые траектории –
параболы
=>
корни
вещественные, неотрицательные и
различные, а фазовые траектории –
параболы

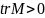 =>
корни
положительные. Особая точка типа
“узел” является неустойчивой, т. е. с
течением времени
=>
корни
положительные. Особая точка типа
“узел” является неустойчивой, т. е. с
течением времени
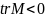 =>
корни
отрицательные. Особая точка типа
“узел” является устойчивой
=>
корни
отрицательные. Особая точка типа
“узел” является устойчивой
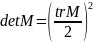 =>
корни
вещественные и равные. В этом случае
особая точка – это вырожденный узел –
дикритический узел (на фазовой плоскости
имеем семейство двойных парабол
относительно
=>
корни
вещественные и равные. В этом случае
особая точка – это вырожденный узел –
дикритический узел (на фазовой плоскости
имеем семейство двойных парабол
относительно
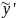 ,
как в случае 1, и относительно
,
как в случае 1, и относительно
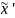 )
)
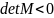 =>
корни
вещественные и различные по знаку.
Особая точка – седло, фазовые траектории
имеют форму гипербол.
=>
корни
вещественные и различные по знаку.
Особая точка – седло, фазовые траектории
имеют форму гипербол.
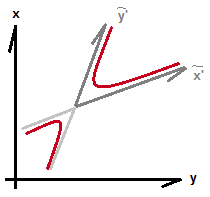
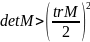 =>
корни
комплексно-сопряжённые,
=>
корни
комплексно-сопряжённые,
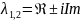
=>
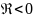 => имеем особую точку типа устойчивый
фокус. Фазовые траектории в виде
спиралей, приближающихся к особой
точке
=> имеем особую точку типа устойчивый
фокус. Фазовые траектории в виде
спиралей, приближающихся к особой
точке
=>
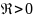 => имеем неустойчивый фокус, спирали
отдаляются от особой точки
=> имеем неустойчивый фокус, спирали
отдаляются от особой точки
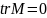 ,
,
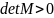 =>
имеем чисто комплексные корни. Особая
точка типа центр, фазовые траектории
имеют форму эллипсов
=>
имеем чисто комплексные корни. Особая
точка типа центр, фазовые траектории
имеют форму эллипсов
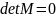 =>
хотя бы один из корней равен нулю. Особые
точки заполняют одну из координатных
осей, фазовые траектории – прямые.
Особые точки здесь безымянные.
=>
хотя бы один из корней равен нулю. Особые
точки заполняют одну из координатных
осей, фазовые траектории – прямые.
Особые точки здесь безымянные.
Водозабор исследования особых точек:
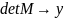
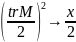
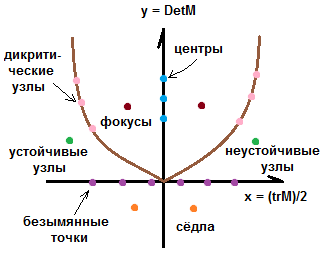
Провести следующее компьютерное исследование:
Задана линеаризованная система дифференциальных уравнений. Подобрать значения коэффициентов матрицы системы так, чтобы получить начало координат как особую точку заданного типа (всех рассмотренных типов с 1-го по 6-й) и в каждом случае построить фазовые траектории.
Замечание: все фазовые точки имеют силу только вблизи к началу системы координат. Иными словами, начальное условие должно задаваться вблизи к началу координат. Для особых точек каждого типа понятие близости к началу координат различается.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Катермина Татьяна Сергеевна |
07.09.2012 Лекция |
Вторую половину курса ведёт Татьяна Сергеевна! Ура!
САМООРГАНИЗАЦИЯ И ОБРАЗОВАНИЕ СТРУКТУР.
РАСПРЕДЕЛЁННЫЕ СИСТЕМЫ.
Точечные модели – это модели, в которых искомые величины зависят только от времени (это все модели, рассмотренные ранее).
Распределённые модели – это модели, в которых величины меняются не только во времени, но и в пространстве.
В дальнейшем будут рассмотрены системы, в которых могут возникать устойчивые пространственные неоднородные связи, возникающие в результате развития неустойчивостей в однородной диссипативной среде (в среде, которая не получает энергии из вне). Такие структуры принято называть диссипативными. В 1952-ом году Алан Тьюринг основал теорию диссипативных сред.
Базовая модель теории распределённых или диссипативных систем описывается следующей системой уравнений:
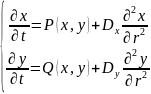
 и
и
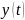 – это, кроме всего прочего, ещё и функции,
описывающие процессы в распределённых
системах
– это, кроме всего прочего, ещё и функции,
описывающие процессы в распределённых
системах
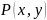 и
и
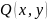 – это функции среды
– это функции среды
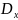 и
и
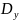 – скорости распределения возмущений
по осям
и
соответственно
– скорости распределения возмущений
по осям
и
соответственно
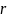 – величина, равная радиальной координате,
– величина, равная радиальной координате,
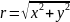 .
.
Иногда данные уравнения называют распределёнными или диффузионными.
Эта модель описывает процессы самопроизвольного возникновения и распространения волн в распределённых системах, которые также называются процессами самоорганизации.
Автоволны
– это периодические самоподдерживающиеся
волны или активности. В зависимости от
видов функций
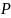 ,
,
 ,
,
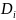 в системе могут возникать следующие
типа поведения и самоорганизации.
в системе могут возникать следующие
типа поведения и самоорганизации.
<вставить рисунки сюда>
5 – Стационарное неоднородное распределение переменных в пространстве диссипативной структуры.
6 – Генерация волн автономным источником импульсной активности. В качестве такого источника могут быть локальные возмущения переменных.
Общим условием развития процессов самоорганизации является появление неустойчивости в исходной распределённой системе. Такие неустойчивости могут возникнуть, если отклонение от состояния равновесия превышает критическое. В частности, такие неустойчивости могут возникнуть в системах с особой точкой типа “седло”, а “неустойчивый узел” может вызвать даже возникновение бегущих волн конечной амплитуды или стоячих волн.
Диссипативная структура, возникающая в результате неустойчивости, в реальном мире может поддерживаться за счёт постоянного притока энергии и вещества. Например, стоячие волны.
Для возникновения диссипативных структур нужно, чтобы уравнение, описывающее процессы в системе, были нелинейными. Кроме того, процессы в системе должны протекать согласовано. Изучением таких систем занимается синергетикой – междисциплинарная область или наука.
