8.2. Дискретні випадкові величини
Випадковою величиною називається така величина, що у результаті випробування може приймати одне зі своїх можливих значень, причому заздалегідь невідомо яке. Наприклад, число народжених дітей протягом доби в Донецьку, зріст людини, витрата електроенергії на підприємстві за місяць, кількість бракованих виробів у партії.
Дискретною називається випадкова величина, що може приймати лише окремі, ізольовані друг від друга значення.
Законом розподілу випадкової величини називається всяке співвідношення, що встановлює зв'язок між можливими значеннями випадкової величини й імовірностями їхньої появи. Закон розподілу можна задавати табличним, графічним, аналітичним способами.
Ряд розподілу – це перелік всіх можливих значень дискретної випадкової величини й відповідних їм імовірностей:
-
…
…
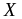
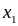
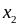
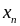
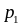
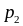
Сума ймовірностей всіх можливих значень дискретної випадкової величини дорівнює одиниці:
.
(8.2.1)
Ряд
розподілу може бути зображений графічно.
Ламану, яку отримаємо, якщо з'єднаємо
точки
,…,
відрізками прямих, називають
багатокутником
розподілу
або полігоном.
Інтегральною
функцією розподілу
(або
функцією розподілу)
називається функція
,
що визначає для кожного значення
імовірність події
,
тобто
.
(8.2.2)
Властивості інтегральної функції розподілу:
Значення інтегральної функції належать відрізку [0;1]:
.
(8.2.3)
Функція – неспадна, тобто
,
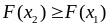якщо
.
,
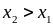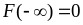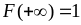.Імовірність того, що випадкова величина прийме значення з напівінтервалу
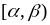(де
),
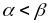дорівнює різниці значень інтегральної
функції на кінцях цього напівінтервалу:
.
(8.2.4)
Математичним сподіванням дискретної випадкової величини називається
.
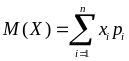(8.2.5)
Якщо значення дискретної випадкової величини утворюють нескінченну послідовність, то
.
(8.2.6)
Властивості математичного сподівання:
,
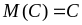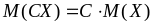для постійної величини
;
(8.2.7)
.
(8.2.8)
Математичне
сподівання є найважливішою з так званих
характеристик положення (центра
групування) випадкової величини, до
яких крім неї належать також мода й
медіана. Модою
дискретної випадкової величини
називається те її значення, що має
найбільшу ймовірність.
Дисперсією випадкової величини називається
.
(8.2.9)
Дисперсію дискретної випадкової величини з скінченним числом значень n можна обчислити за формулою:
.
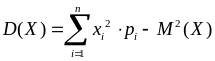(8.2.10)
Властивості дисперсії:
,
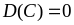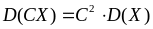для постійної величини
;
(8.2.11)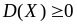
,
(8.2.12)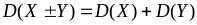
(для незалежних
).
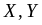(8.2.13)
Середнім квадратичним відхиленням випадкової величини називається (арифметичний) корінь квадратний із дисперсії:
.
(8.2.14)
Дисперсія й середнє квадратичне відхилення є мірою розсіювання значень випадкової величини навкруг математичного сподівання.
Приклад
8.2.1
У відділі побутової техніки 4 людини.
Для кожної людини ймовірність того, що
вона звернеться до консультанта, дорівнює
0,4. а) Скласти закон розподілу
випадкової величини
– числа людей, які можуть звернутися
до консультанта, б) побудувати
багатокутник розподілу, в) побудувати
інтегральну функцію розподілу
і її графік; г) обчислити числові
характеристики
,
,
,
.
Розв’язання. а) Випадкова величина – число людей, які можуть звернутися до консультанта – може приймати значення 0, 1, 2, 3, 4. Для кожного можливого значення випадкової величини знайдемо ймовірність за формулою Бернуллі (8.1.15):
;
;
;
;
.
Таким чином, ряд розподілу має вигляд:
|
0 |
1 |
2 |
3 |
4 |
|
0,1296 |
0,3456 |
0,3456 |
0,1536 |
0,0256 |
Перевірка: 0,1296 + 0,3456 + 0,3456 + 0,1536 + 0,0256 = 1.
б) Багатокутник розподілу ймовірностей має вигляд:
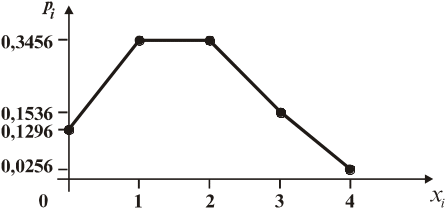
Рис. 8.2.1 ‑ Полігон
в) Побудуємо інтегральну функцію розподілу :
Нехай
.
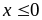Ліворуч від такого
немає значень випадкової величини
,
значить подія
неможлива, а її ймовірність дорівнює
нулю, таким чином,
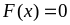.Нехай
.
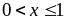Через те, що випадкова величина
може прийняти тільки одне можливе
значення 0 з імовірністю 0,1296, то
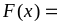0,1296.Нехай
.
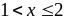У цьому випадку випадкова величина
може прийняти можливе значення 0 з
імовірністю 0,1296, або можливе значення
1 з імовірністю 0,3456. Оскільки ці події
несумісні, то за теоремою додавання
ймовірностей імовірність події
дорівнює сумі ймовірностей цих подій.
Тому, що
,
то
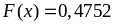.Нехай
.
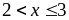Тоді аналогічно
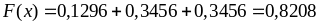.Нехай
.
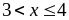Тоді
.Нехай
.
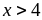Тоді подія
достовірна, значить
.
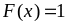Таким чином, функція розподілу та її графік мають вигляд:
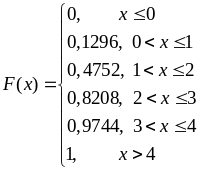
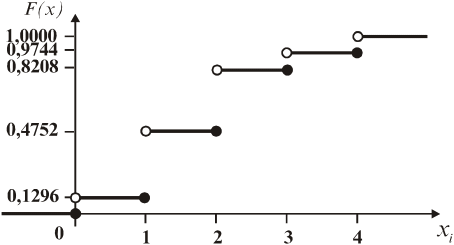
Рис. 8.2.2 – Графік функції розподілу
Графік інтегральної функції розподілу дискретної випадкової величини має східчастий вигляд, розриви при значеннях х, що збігаються з можливими значеннями випадкової величини; величини стрибків дорівнюють значенням ймовірностей, що відповідають можливим значеннями дискретної випадкової величини.
г) Знайдемо
математичне сподівання випадкової
величини
та випадкової величини
за формулою (8.2.5):
.
.
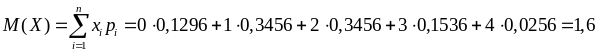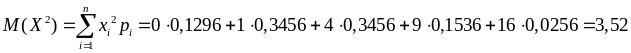Тоді
дисперсія згідно (8.2.9):
,
середнє квадратичне відхилення за
(8.2.14):
.
Найбільша ймовірність
відповідає двом значенням випадкової
величини (
і
),
значить розподіл є двомодальним й
.
Зауважимо, що приклад 8.2.1 г) відповідає завданню 8.2 контрольної роботи, у якому для обчислення невідомої ймовірності (у другому рядку таблиці розподілу ймовірностей випадкової величини ) треба застосувати формулу (8.2.1).
Література: [1, с. 516 ‑ 525], [4, с. 529 – 532], [16], [18], [20].