1 Метод разности средних уровней

Самый простой подход заключается в разбиении анализируемого ряда на две при­мерно равные по числу членов части, каждая из которых рассмат­ривается как некоторая самостоятельная выборочная совокупность данных. Испытание разности средних, исчисленных для каждой из этих совокупностей, покажет, существенно ли различаются между собой средние или это расхождение можно приписать действию случайности и, таким образом, заключить, что тренд отсутствует.

Поскольку число членов ряда, как правило, довольно незначи­тельно, то воспользуемся методом проверки, разработанным для малых выборок (предполагается, что они имеют нормальное рас­пределение).

Итак, ряд разбивается на две части. Уровни каждой из них рассматриваются как две выборки. Первая имеет среднюю вторая − . Необходимо проверить гипотезу о существенности разности − . Проверка данной гипотезы опирается на t - критерий Стьюдента.

В самом простом случае — при равенстве или несущественном различии дисперсий двух исследуемых совокупностей – t -статистика исчисляется, как известно, с помощью выражения

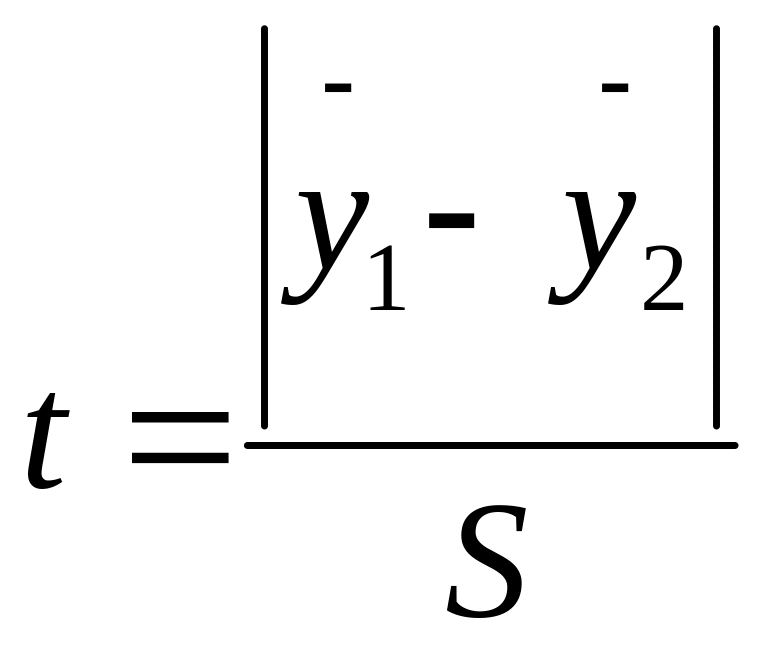, (1)

где и − средние для первой и второй совокупности наблю­дений (в нашем случае − для первой и второй поло­вины ряда);

n₁ и n₂ − числа наблюдений в этих группах;

s − среднее квадратическое отклонение разности сред­них.

При гипотеза об отсутствии тренда отвергается, при эта гипотеза принимается. Здесь t – рас­четное значение t-критерия, – табличное ее значение при вероятности ошибки, равной (приложение Б).

Значение берется с числом степеней свободы, равным n₁ + n₂ − 2. Значение S можно определить на основе средней взвешенной величины дисперсий отдельных совокупностей;

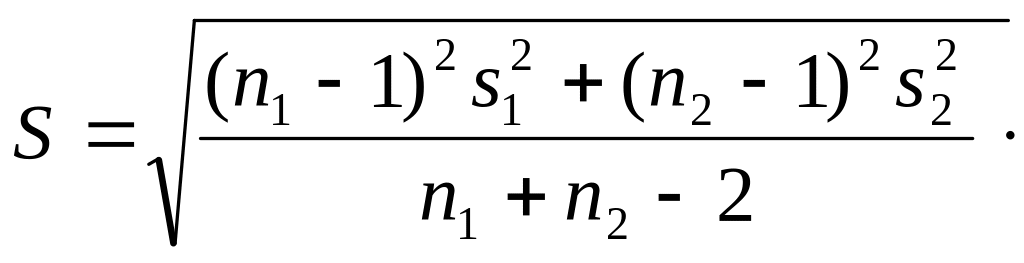
(2)

Заметим, что при оценивании дисперсий для первой и второй совокупности, и , берется число степеней свободы, равное n₁ – 1 и n₂ – 1 соответственно.

При применении формулы (1) пред­полагается, что дисперсии двух совокупностей незначительно раз­личаются между собой. Проверка однородности дисперсий реали­зуется с помощью F − критерия Фишера, который основан на срав­нении расчетного отношения

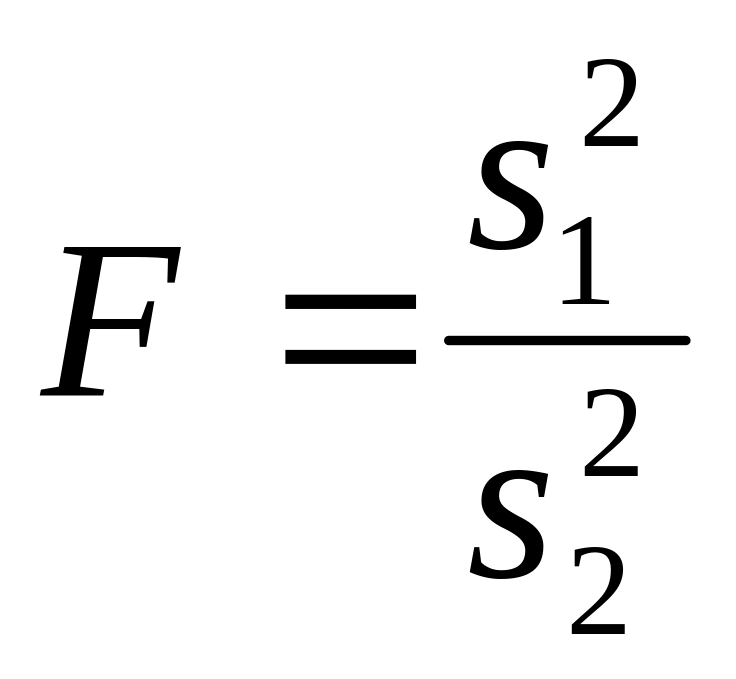(в числителе приводится большая дисперсия) (3)

с табличным. Если расчетное значение F меньше, чем табличное (приложение 3), при заданном уровне вероятности, то можно принять гипотезу о равенстве дисперсий. Если же F больше, чем табличное значение, то гипотеза о равенстве дисперсий отклоняется и, следовательно, формула (1) для испытания разности средних не может быть применена.

Пример 1. Пусть динамический ряд состоит из натуральных чисел 1, 2, ..., 10. Тогда средняя для первой по­ловины ряда равна 3, а для второй − 8. Воспользуемся t-статисти­кой Стьюдента. Для случая, когда n₁ = n₂, формулу (1) можно представить в виде

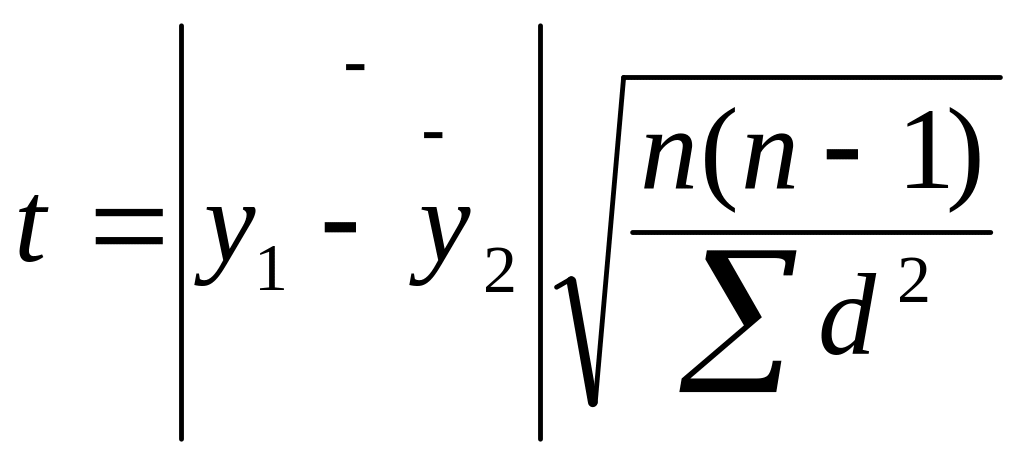, (4)

где ; − сумма квадратов отклонений от общей средней. По дан­ным нашего примера Следовательно,

Табличное значение при вероятности 0,95 равно 2,307. Таким образом, t_расч.>t_a и гипотеза об отсутствии тренда в средних отвер­гается (Приложение Б).

Рассмотренный выше метод в ряде случаев дает вполне прием­лемые результаты. Однако следует отметить, что ему свойственны весьма существенные дефекты. Прежде всего, он применим только для рядов с монотонной тенденцией. Если же ряд меняет общее направление развития, то точка поворота тенденции может ока­заться близкой к середине ряда, в силу этого средние двух отрез­ков ряда будут близки и проверка может не показать наличие тренда. Вместе с тем можно выдвинуть и более серьезное возраже­ние, основанное на том, что величина среднего квадратического отклонения, с которой сравнивается разность средних в (1), зави­сит в динамическом ряду не только от колеблемости уровней, но и от самого тренда. Иначе говоря, существование тренда сказы­вается на показателе среднего квадратического отклонения. Сама же разность средних в значительной мере будет определять­ся тем, какой угол наклона имеет тренд.