217

Мартьянова А.Е. Математические методы моделирования в геологии

АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

А.Е. МАРТЬЯНОВА

Математические методы моделирования в геологии

Часть I

Учебное пособие для студентов направления

650100 «Прикладная геология»

Астрахань

2008

УДК 518 : 55

ББК 26.3

Рецензент:

зав. каф. ГНГ АГТУ,

д.г.-м.н., проф. Н.Н. Гольчикова

Учебное пособие рассмотрено и рекомендовано к печати на заседании кафедры ____________ (протокол № от г.)

Мартьянова А.Е. Математические методы моделирования в геологии. Часть I: Учебное пособие для студентов направления 650100 «Прикладная геология». – Астрахань: АГТУ, 2008. – 218 с.

Настоящее учебное пособие подготовлено по материалам учебного курса, посвященного математическим методам в геологии, который читался автором для направления 650100 «Прикладная геология». В пособии рассмотрены сущность и условия применения одномерных, двумерных и многомерных статистических моделей, методы математического описания пространственных геологических закономерностей. В процессе освоения материала пособия предполагается выполнение рассматриваемых примеров и задач на компьютере в двух популярных программных пакетах: электронных таблицах Excel корпорации Microsoft и статистическом пакете STATISTICA фирмы StatSoft.

СОДЕРЖАНИЕ

ПРЕДИСЛОВИЕ 3

ВВЕДЕНИЕ 5

ЛАБОРАТОРНАЯ РАБОТА № I. ОДНОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. СУЩНОСТЬ И УСЛОВИЯ ПРИМЕНЕНИЯ. ПРОСТЕЙШИЕ ПРЕОБРАЗОВАНИЯ КОЛИЧЕСТВЕННОЙ ГЕОЛОГИЧЕСКОЙ ИНФОРМАЦИИ 21

ЛАБОРАТОРНАЯ РАБОТА № II. ОДНОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ, ИСПОЛЬЗУЕМЫЕ В ГЕОЛОГИИ. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ. ИНТЕРВАЛЬНЫЕ ОЦЕНКИ СВОЙСТВ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ 46

ЛАБОРАТОРНАЯ РАБОТА № III. ОДНОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГЕОЛОГИЧЕСКИХ ГИПОТЕЗ 81

ЛАБОРАТОРНАЯ РАБОТА № IV. ОДНОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. ОДНОФАКТОРНЫЙ И ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ В ГЕОЛОГИИ 154

ЛАБОРАТОРНАЯ РАБОТА № V. ДВУМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ. РЕГРЕССИОННЫЙ АНАЛИЗ 175

ПРЕДИСЛОВИЕ

Настоящее учебное пособие подготовлено по материалам учебного курса, который читался автором для студентов направления 650100 «Прикладная геология» по дисциплине «Математические методы моделирования в геологии». Пособие является уже вторым изданием и в значительной мере расширено и дополнено.

Пособие состоит из введения, списка литературы, приложений и десяти разделов: Лабораторная работа № I. «Одномерные статистические модели. Сущность и условия применения. Простейшие преобразования количественной геологической информации». Лабораторная работа № II. «Одномерные статистические модели. Статистические характеристики, используемые в геологии. Законы распределения. Интервальные оценки свойств геологических объектов». Лабораторная работа № III. «Одномерные статистические модели. Статистическая проверка геологических гипотез». Лабораторная работа № IV. «Одномерные статистические модели. Однофакторный и двухфакторный дисперсионный анализ в геологии». Лабораторная работа № V. «Двумерные статистические модели. Корреляционный анализ. Регрессионный анализ». Лабораторная работа № VI. «Многомерные статистические модели. Многомерный корреляционный анализ. Множественная регрессия». Лабораторная работа № VII. «Многомерные статистические модели. Кластерный анализ. Факторный анализ». Лабораторная работа № VIII. «Многомерные статистические модели. Задачи распознавания образов в геологии». Лабораторная работа № IX. «Моделирование пространственных переменных. Аппроксимация поверхностей тренда полиномами». Лабораторная работа № X. «Оптимизация». Каждый раздел содержит примеры, решение которых подробно рассматривается в пособии и задачи, для решения которых, как правило, приводятся необходимые указания и теоретические сведения. В основу учебного пособия положены материалы, подобранные из источников [1, 9 – 11, 17]. Обращение этим к источникам определяет круг используемых в пособии примеров и задач, решение которых рассматривается на основе использования современного программного обеспечения: электронных таблиц Excel корпорации Microsoft и статистического пакета STATISTICA 6.0 фирмы StatSoft, Inc. При рассмотрении теоретических вопросов широко использовались источники [4 – 6, 10 – 12, 19].

Для дополнительного изучения возможностей рассматриваемого программного обеспечения по обработке статистических данных можно порекомендовать обращение к источникам [2, 3, 7, 8, 16, 18, 20].

В конце пособия приводится список контрольных вопросов.

Из источника [3] в приложении XIII приводится англо-русский словарь терминов пакета STATISTICA и статистических терминов.

В приложении XIV приводится краткий справочник по основным функциям Excel, используемым в вычислениях, составленный по справочным материалам программы.

В приложении XV приводится краткий справочник по использованию пакета анализа Excel.

Учебное пособие адресовано студентам-геологам, изучающим математические методы моделирования в геологии, но также может быть полезно преподавателям и специалистам.

Хочу поблагодарить студентов потока ДХГ-III Астраханского государственного технического университета, во многом благодаря которым состоялось данное учебное пособие.

ВВЕДЕНИЕ

ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ

На современном этапе развития естественных наук, под влиянием научно-технического прогресса происходят существенные изменения методов научных экспериментов, анализа и обобщения получаемых результатов. Этому способствуют не только расширившиеся возможности фундаментальных наук, но также бурное развитие электронно-вычислительной техники и комплексной автоматизации самых разнообразных видов человеческой деятельности. В последние десятилетия наблюдается глубокое проникновение математических методов исследования во все отрасли естественных наук, что способствовало исключительным успехам некоторых из них, например биологии, метеорологии и др. Для успешного развития геологических наук необходимо также использовать полный арсенал существующих прогрессивных научных и технических средств, включая математические методы и ЭВМ.

Современная геология уже не может ограничиваться изучением лишь качественных сторон явлений и процессов, а должна выявлять их количественные характеристики, обеспечивая тем самым более высокий научный уровень исследования земных недр. Необходимость применять математические методы обработки, анализа и обобщения данных все острее ощущается не только при прогнозировании, поисках, разведках и оценках месторождений полезных ископаемых, но и вообще при проведении любых геологических исследований. Так, например, палеонтологические, стратиграфические, структурно-геологические, литологические, петрографические, минералогические, геохимические, геоморфологические и другие геологические исследования, которые в недавнем прошлом ограничивались чисто описательными приемами, требуют в настоящее время использования меры и числа.

Ежегодно в геологических организациях страны накапливается колоссальный эмпирический материал – миллионы количественных определений химического состава различных минералов и их агрегатов, химического и минерального составов горных пород и полезных ископаемых, их физических, горно-технологических и других свойств, требующих применения ЭВМ для обработки и обобщений с целью более полного извлечения содержащейся в них полезной информации.

Острую необходимость внедрения математических методов в практику геологоразведочных работ испытывают производственные геологические организации в связи с возросшими требованиями промышленности к конкретности и достоверности геологоразведочных данных. Так, в соответствии с действующими положениями количественные оценки прогнозных ресурсов полезных ископаемых должны быть обоснованы уже по данным геологических съемок с уточнениями цифр прогнозных ресурсов (а затем запасов) на каждой из последующих стадий геологоразведочных работ.

Резкое увеличение количественной информации, получаемой в процессе геологической съемки, поисков и разведки полезных ископаемых, вызвало необходимость разработки принципиально новых способов ее хранения, поиска, обработки и анализа с помощью ЭВМ.

С учетом все возрастающей роли математических методов и широкого использования ЭВМ во всех отраслях геологической науки становится очевидным значение данной дисциплины в образовании современного геолога, специалиста по геологической съемке, поискам и разведке месторождений полезных ископаемых.

Курс «Математические методы в геологии» имеет своей целью ознакомить студентов с особенностями геологических образований и процессов, как объектов математического изучения и моделирования, со спецификой геологических задач, решаемых с помощью математических методов, с возможностями различных математических методов и факторами, влияющими на эффективность их использования.

Задачи изучения дисциплины определяются требованиями геологоразведочной службы страны и квалификационной характеристикой молодого специалиста. После изучения курса он должен:

1) знать основные принципы геолого-математического моделирования, главные типы моделей и особенности их применения в различных областях геологии;

2) владеть методами математической обработки геологической, геохимической и геофизической информации;

3) уметь формулировать геологические задачи в виде, пригодном для их решения математическими методами, и выбирать наиболее эффективные методы их решения.

ХАРАКТЕР ГЕОЛОГИЧЕСКОЙ ИНФОРМАЦИИ

Многообразие геологических объектов и методов их изучения приводит к тому, что результатом геологических исследований является весьма разнородная по характеру информация – словесная (описательная), графическая (картографическая), цифровая.

Недоступность геологических объектов для непосредственного наблюдения служит причиной того, что геология, как теоретическая дисциплина, развивалась в условиях практически полного отсутствия экспериментальных данных и на протяжении многих лет считалась чисто описательной наукой.

До недавнего времени геологическая информация имела в основном качественный характер, то есть она заключалась в словесном описании и зарисовках, в то время как число и мера играли довольно скромную роль, выполняя главным образом иллюстративные функции. Теоретические выводы геологов, основанные на личном опыте и интуиции, отражали не только реальные свойства природных образований и явлений, но и, в определенной степени, субъективные представления авторов. Это привело к тому, что существующие в геологии понятия и определения часто неоднозначны, неконкретны, сформулированы на языке, полном образных выражений, сравнений, аналогий. В геологической литературе имеется несколько десятков определений понятий «минерал», «горная порода», «формация» и более ста определений понятия «фация».

Весьма распространенной формой обобщения знаний о свойствах геологических объектов являются классификации и группировки. Однако в основу большинства из них положены качественные признаки, причем набор этих признаков и количество групп в классификациях неодинаковы. Например, для разделения изверженных пород по минеральному и химическому составам используется, как минимум, пять различных классификаций, предложенных С. Мишель-Леви, Г. Розенбушем, Ф.Ю. Левинсоном-Лессингом, П. Ниггли и А.Н. Заварицким.

Неоднозначно определенные геологические понятия берутся за основу условных обозначений при составлении графических геологических документов – зарисовок, разрезов, планов, карт. В результате этого картографическая геологическая информация также является неоднозначной, и нередко геологические карты, составленные в одном и том же масштабе на одну и ту же территорию, но в разные годы и различными исследователями, существенно отличаются друг от друга.

Количественная (цифровая) геологическая информация, объем которой резко возрос в последние годы, также имеет некоторые специфические особенности. Ввиду выборочного метода изучения и сложности геологических объектов она отражает их свойства не полностью, а из-за технических погрешностей измерения – не всегда достаточно точно.

Определенная неоднозначность возникает также за счет того, что некоторые свойства геологических объектов иногда могут быть выражены различными числовыми характеристиками. Так, например, изучение степени окатанности песчаных зерен и галек позволяет судить о характере их транспортировки и расстояниях до источника сноса. Однако в качестве оценки степени окатанности могут быть использованы следующие величины: частное от деления радиуса кривизны самого острого конца песчинки или гальки на ее средний радиус; отношение среднего радиуса максимальных окружностей, описывающих вершины всех углов границы в ее проекции на плоскости, к радиусу наибольшего круга, вписанного в эту проекцию; и т.д.

При изучении полезных ископаемых могут анализироваться валовые содержания химических элементов, содержания их оксидов, сульфидов или других химических соединений, содержания минералов-носителей полезных компонентов или другие количественные показатели качества руд. Для большинства рудных месторождений чаще всего используются содержания химических элементов, для россыпных месторождений – содержания полезных минералов, а для некоторых месторождений – содержания различных соединений металлов, обладающих резко контрастными технологическими свойствами. Так, при переработке оловянных руд значительно легче извлекаются в концентраты оксиды олова по сравнению с сульфидами, в металлургических процессах железных руд силикаты железа не выплавляются, а уходят в шлаки и т.д., поэтому для выбора наиболее подходящего вида числовых измерений прежде всего следует установить, какая из возможных количественных характеристик наиболее полно выражает изменения интересующего нас свойства.

МОДЕЛИРОВАНИЕ В ГЕОЛОГИИ

Материальные системы, как объекты изучения, принято разделять на хорошо и плохо организованные.

Хорошо организованные системы состоят из ограниченного количества элементов, между которыми существуют строго определенные и однозначные зависимости. К этим системам можно отнести простейшие химические и физические процессы, механизмы, приборы и т.п. Их свойства и состояния могут быть количественно описаны с помощью законов физики и химии.

К плохо организованным системам относятся сложные природные объекты и явления, на состояние и свойства которых влияет множество факторов различной природы. Типичными плохо организованными системами являются живые организмы и их сообщества, а также большинство объектов, изучаемых науками о Земле. При изучении них систем в их структуре удается установить лишь отдельные закономерности, то есть тенденции, не поддающиеся строгому количественному выражению.

Основным методом изучения плохо организованных систем является моделирование, когда непосредственный объект изучения заменяется его упрощенным аналогом – моделью.

По характеру моделей выделяют предметное и знаковое (информационное) моделирование.

Предметным называется моделирование, в ходе которого исследование ведется на модели, воспроизводящей определенные геометрические, физические, динамические либо функциональные характеристики объекта.

При знаковом моделировании в качестве моделей выступают схемы, чертежи, формулы, мысли, высказанные или записанные на каком-либо языке.

В зависимости от того, какие особенности объекта изучаются, различают модели его структуры и поведения (функционирования). Первые используются для изучения статичных систем (то есть свойств материальных предметов), а вторые – для исследования динамичных систем (то есть процессов).

Рассмотренные выше свойства геологических образований и процессов исключают возможность широкого применения предметного моделирования в геологии, хотя в последние годы все чаще предпринимаются попытки воспроизведения в лабораторных условиях отдельных элементов геологических процессов. Появились такие научные направления, как экспериментальная геотектоника, петрология, геохимия. Большие успехи экспериментальной минералогии привели к разработке технологических процессов получения синтетического кристаллосырья в промышленных масштабах.

При промышленной оценке месторождений предметное моделирование применяется для изучения технологических свойств руд по лабораторным и полупромышленным пробам. При этом лабораторные установки, имитирующие процесс переработки руды, являются действующими моделями оборудования будущей обогатительной фабрики.

Однако ведущую роль в науках о Земле играют различные методы знакового (информационного) моделирования. По характеру информации их можно разделить на словесные, графические и математические.

К словесным моделям можно отнести многочисленные классификации, понятия и определения, которыми изобилуют все геологические дисциплины.

К графическим моделям следует отнести все разнообразные графические геологические документы – карты, планы, разрезы, проекции и т.п., в связи с тем, что они отражают свойства реальных объектов недр упрощенно и приблизительно.

В качестве математических моделей в геологии используются числа и формулы, описывающие взаимосвязи и закономерности изменения свойств геологических образований или параметров геологических процессов.

В последние годы в связи с широким внедрением в практику геологических исследований моделирования на ЭВМ с использованием разнородной геологической информации границы между этими видами моделей становятся в известной степени условными. Картографическая информация с помощью номинальной шкалы измерений переводится в цифровую, а результаты замеров при геохимических и геофизических съемках с помощью графопостроителей или графических дисплеев изображаются в виде карт изолиний.

ТИПЫ ГЕОЛОГО-МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

По принципу построения математической модели различают статическое и динамическое моделирование.

Статическое моделирование заключается в математическом описании свойств исследуемых объектов по результатам их изучения выборочным методом на основе индуктивного обобщения эмпирических данных.

Динамическое моделирование использует приемы дедуктивного метода, когда свойства конкретных объектов выводятся из общих представлений о его структуре и законах, определяющих его свойства.

В настоящее время в практике геологических исследований применяются главным образом статические модели. Это обусловлено сложностью и разнообразием геологических объектов и трудностью описания геологических процессов даже в самых общих чертах.

Статическое моделирование сводится к:

• преобразованию геологической информации в вид, удобный для анализа;

• выявлению закономерностей в массовых и в известной степени случайных замерах свойств изучаемых объектов;

• математическому описанию выявленных закономерностей (составлению математической модели);

• использованию полученных количественных характеристик для решения конкретных геологических задач – проверки геологических гипотез, выбору методов дальнейшего изучения объекта и т.п.;

• оценке вероятности возможных ошибок в решении поставленной задачи за счет выборочного метода изучения объекта.

Порядок решения геологических задач на основе динамического моделирования иной. Исходя из общих соображений о генезисе изучаемого объекта строится теоретическая математическая модель процесса его образования, учитывающая основные факторы, влияющие на конечный результат этого процесса, то есть на свойства объекта.

Такая модель обычно может быть предложена лишь в самом общем виде, поскольку параметры процесса неизвестны. Эти параметры определяют путем перебора различных вариантов и сравнения теоретических реализации процесса с фактическими свойствами изучаемого объекта, установленными эмпирическим путем. Динамическое моделирование сопряжено с большим объемом довольно сложных вычислений и возможно лишь на базе ЭВМ.

По характеру связи между параметрами и свойствами изучаемых объектов математические модели разделяются на детерминированные и статистические.

Детерминированные модели выражают функциональные связи между аргументом и зависимыми переменными. Они записываются в виде уравнений, в которых определенному значению аргумента соответствует только одно значение переменной. При моделировании геологических объектов детерминированные модели используются редко. Это объясняется тем, что они плохо согласуются с реальными явлениями, в которых функциональные связи сохраняются лишь в узких, весьма ограниченных областях.

Статистическими моделями называются математические выражения, содержащие, по крайней мере, одну случайную компоненту, то есть такую переменную, значение которой нельзя предсказать точно для единичного наблюдения. Их весьма широко используют для целей математического моделирования, поскольку они хорошо учитывают случайные колебания экспериментальных данных.

Многообразие геологических задач и объектов изучения вызвало необходимость использования при геолого-математическом моделировании методов из разных разделов математики: теории вероятностей и математической статистики, теории множеств, теории групп, теории информации, теории графов, теории игр, матричной и векторной алгебры, дифференциальной геометрии и др. При этом одна и та же задача может быть решена разными методами, а в некоторых случаях для решения одной задачи необходимо использовать комплекс методов из разных разделов математики. Это создает определенные трудности при систематизации математических методов, применяемых в геологии.

Вместе с тем по типу решаемых задач, набору используемых для этого математических методов и главным допущениям относительно свойств геологических объектов все геолого-математические модели отчетливо разделяются на две группы.

В первую группу объединяются модели, использующие главным образом математический аппарат теории вероятностей и математической статистики. В них геологические объекты предполагаются внутренне однородными, а изменения их свойств в пространстве – случайными, не зависящими от места замера. Такие модели можно условно назвать статистическими. В зависимости от количества одновременно рассматриваемых свойств они разделяются на одномерные, двумерные и многомерные.

Статистические модели обычно используются для:

• получения по выборочным данным наиболее надежных оценок свойств геологических объектов;

• проверки геологических гипотез;

• выявления и описания зависимостей между свойствами геологических объектов;

• классификации геологических объектов;

• определения объема выборочных данных, необходимого для оценки свойств геологических объектов с заданной точностью.

Во вторую группу можно объединить модели, рассматривающие свойства геологических объектов как пространственные переменные. В этих моделях предполагается, что свойства геологических объектов зависят от координат точки замера, а в изменении этих свойств в пространстве существуют определенные закономерности. При этом, наряду с некоторыми вероятностными методами (случайные функции, временные ряды, дисперсионный анализ), применяются также приемы комбинаторики (полиномы), гармонического анализа, векторной алгебры, дифференциальной геометрии и других разделов математики.

Для изучения пространственных геологических переменных используются приемы как статического, гак и динамического моделирования.

Модели пространственных геологических переменных используются для решения задач, связанных с:

• проверкой гипотез о закономерностях размещения геологических объектов относительно друг друга;

• проверкой гипотез о характере процессов формирования геологических образований;

• выделением аномалий в геологических и геофизических полях;

• классификацией геологических объектов по особенностям их внутреннего строения;

• разработкой приемов интерполяции и экстраполяции при оконтуривании геологических объектов;

• выбором оптимальной густоты и формы сети наблюдений при изучении геологических объектов.

ПРИНЦИПЫ И МЕТОДЫ ГЕОЛОГО-МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Применение математического моделирования в геологии сопряжено с рядом трудностей.

Математическая модель, как и любая другая, является упрощенным аналогом исследуемого объекта. Из-за сложности геологических объектов ни одна математическая модель не может воспроизвести все их свойства. Поэтому для описания различных свойств одного и того же объекта часто приходится использовать различные математические модели. При этом необходимо убедиться в том, что выбранная модель достаточно полно отражает именно те свойства объекта, которые непосредственно влияют на решение поставленной задачи.

Математические модели не могут исчерпывающе полно характеризовать изучаемые свойства. Они основаны на определенных допущениях о характере свойств объекта моделирования. Поэтому необходимо следить за тем, чтобы эти допущения не приводили к принципиальному искажению реальных свойств объекта в рамках поставленной задачи. В связи с тем, что встречающиеся в практике геологических исследований задачи также весьма разнообразны, может возникнуть ситуация, когда для моделирования одного и того же свойства объекта необходимо использовать различные модели.

Определенные сложности иногда возникают также из-за отсутствия четких границ геологических совокупностей и рассмотренных выше особенностей их изучения.

Итак, решение геологических задач на основе математического моделирования представляет собой довольно сложный процесс, в котором можно выделить следующие этапы:

1) формулировка геологической задачи;

2) определение геологической совокупности, то есть установление границ геологического объекта или временного интервала геологического процесса;

3) выявление главных свойств объекта или параметров процесса в рамках поставленной задачи;

4) переход от геологической совокупности к опробуемой и выборочной с учетом особенностей методов исследования;

5) выбор типа математической модели;

6) формулировка математической задачи в рамках выбранной математической модели;

7) выбор метода решения математической задачи;

8) решение математической задачи на основе вычисления параметров математической модели объекта;

9) интерпретация полученных результатов применительно к геологической задаче;

10) оценка вероятности и величины возможной ошибки за счет неадекватности модели и объекта.

Таким образом, этапу собственно математического моделирования предшествуют этапы создания геологической модели (опробуемой и выборочной геологической совокупности). Поэтому модели, используемые для решения геологических задач математическими методами, можно назвать геолого-математическими.

Справедливость конечного вывода при решении задач на основе геолого-математического моделирования зависит от правильности решений, принимаемых на каждом этапе. Нетрудно заметить, что решения на большинстве этапов принимаются исходя из особенностей геологических задач и свойств геологических объектов, поэтому они полностью находятся в компетенции геолога. Консультант математик может оказать существенную помощь геологу лишь при выборе метода решения математической задачи. Как показал многолетний опыт, большинство ошибок, допускавшихся при использовании математических методов в геологии, было обусловлено не слабой математической подготовкой геологов, а тем, что не учитывалась специфика геологических объектов и задач. Поэтому при изложении дальнейшего материала на эти аспекты геолого-математического моделирования обращено особое внимание.

МЕТОДЫ ИЗУЧЕНИЯ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ

Недоступность геологических образований и процессов для непосредственного наблюдения обусловила широкое распространение в практике геологических исследований выборочных методов изучения с помощью естественных и искусственных обнажений, в пределах которых отбираются образцы и пробы для различных исследований и анализов. Локальные площади наблюдений и отбираемые пробы несопоставимо малы, по сравнению с площадями и объемами недр, на которые распространяются наблюденные данные. В связи с этим возникают проблемы пространственного размещения пунктов локальных наблюдений, систематизации выборочных данных и их распространения на прилегающие объемы недр.

О свойствах всей геологической совокупности геолог судит по какой-то ее части, доступной для наблюдения и опробования, которую М. Розенфельд предложил назвать опробуемой совокупностью. Степень соответствия свойств опробуемой совокупности и изучаемой геологической совокупности зависит от расположения, густоты и общего количества точек наблюдений, а также от размеров, ориентировки, формы, объема отбираемых проб или способа измерения данного свойства.

Выделяют три основные системы расположения точек наблюдения: равномерное, случайное и многостадийное опробование.

Наибольшее распространение имеет равномерное опробование, при котором точки наблюдений в плоскости изучаемого объекта распределяются по правильной геометрической сети. Такое опробование позволяет с одинаковой детальностью изучить все части изучаемого объекта, поэтому оно является основным при поисках и разведке месторождений полезных ископаемых.

Случайное опробование обычно применяется в тех случаях, когда исследователя не интересуют закономерности изменения изучаемого свойства в пространстве или достоверно известно, что таких закономерностей нет, а также тогда, когда невозможно или затруднительно создать сеть равномерных наблюдений. Так, например, при геологическом картировании в гористой местности пробы берутся преимущественно из естественных обнажений, размещение которых в пределах изучаемой площади близко к случайному. Случайный способ рекомендуется также при отборе проб для контрольных анализов.

Многостадийное опробование применяется для изучения свойств сложных геологических объектов на разных масштабных уровнях их строения. Для этого объект разделяется на участки, соответствующие элементам его неоднородности, в которых, в свою очередь, выделяются более мелкие элементы неоднородности и т.д. В пределах каждого участка опробуется только определенная часть элементарных участков более высокого порядка. За счет этого общее количество наблюдений при многостадийном опробовании существенно сокращается по сравнению с равномерным. Многостадийное опробование применяется при составлении ландшафтных карт. Сначала по результатам дешифрирования космоснимков масштабов 1:500000–1:200000 производится районирование территории по типам ландшафтов, затем в пределах каждого из этих типов выделяются ландшафты водоразделов, склонов, речных долин и т. п.

Для определения границ элементарных ландшафтов используются аэрофотоснимки масштаба 1:50000, а их основные характеристики – состав и мощность рыхлых отложений, тип почвы и растительности – оцениваются путем изучения так называемых ключевых участков, то есть относительно небольших по площади участков, где проявлены все особенности данного ландшафта.

Каждой геологической совокупности может быть поставлен в соответствие набор числовых характеристик, полученных в результате измерения или анализа каких-либо свойств геологических объектов. Такие наборы числовых характеристик называются выборочными (статистическими) совокупностями.

Для правильного решения поставленных геологических задач принципиальное значение имеет однозначное и четкое определение соотношений геологической и выборочной совокупностей.

Для определения конкретной геологической совокупности необходимо, прежде всего, установить ее элементарные составляющие (то есть изучаемые объекты), границы и виды последующих числовых измерений.

Объекты (элементарные составляющие) и границы геологических совокупностей устанавливаются геологом в зависимости от целей и задач исследований. По мнению У. Крамбейна, элементарные составляющие геологических совокупностей можно разделить на две большие группы: образованные первичными индивидами (объектами) или наборами исходных объектов.

К совокупностям, образованным первичными индивидами (объектами), относятся совокупности ископаемых организмов, минералов в шлихах или шлифах и др. По каждому из таких объектов измеряется одно свойство, несколько свойств или оцениваются средние значения свойств в группировках изучаемых объектов. К совокупностям, образованным наборами исходных объектов, относятся совокупности образцов или проб, по которым определяют физико-химические свойства, их гранулометрический состав, содержания полезных или вредных компонентов и др. В таких наборах свойства каждого исходного объекта не измеряются, а оцениваются средние значения тех или иных свойств в объемах проб или образцов. Отличительной особенностью этой группы совокупностей является зависимость числовых характеристик свойств от размеров и объемов проб.

ЛАБОРАТОРНАЯ РАБОТА № I. ОДНОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. СУЩНОСТЬ И УСЛОВИЯ ПРИМЕНЕНИЯ. ПРОСТЕЙШИЕ ПРЕОБРАЗОВАНИЯ КОЛИЧЕСТВЕННОЙ ГЕОЛОГИЧЕСКОЙ ИНФОРМАЦИИ

СУЩНОСТЬ И УСЛОВИЯ ПРИМЕНЕНИЯ

Геологические исследования в большинстве случаев основаны на изучении свойств геологических образований путем замеров в отдельных точках непосредственно на месте их залегания или путем анализа образцов и проб, отобранных в отдельных участках. При этом выборочные наблюдения относятся к элементарно малым пространственно разобщенным объемам недр (в искусственном или естественном обнажении), а выводы, полученные по ним, распространяются на весь изучаемый объем.

Изучая сложные природные объекты выборочными методами, геологи всегда учитывали возможность получения ошибочных результатов по ограниченному количеству наблюдений. Поэтому первые попытки математического моделирования в геологии связаны с использованием математического аппарата теории вероятностей и математической статистики, который обеспечивает возможность получения наиболее надежных выводов по выборочным данным и позволяет оценить точность этих выводов.

В основе статистического моделирования лежат два понятия: о генеральной совокупности – множестве возможных значений определенного признака изучаемого объекта или явления и о выборке – совокупности наблюденных значений этого признака. Оба понятия фактически совпадают с понятиями геологической и опробуемой совокупности.

При использовании статистической модели геологические объекты рассматриваются как совокупности бесконечно большого количества элементарных участков, каждый из которых соответствует по размеру отдельной пробе или месту единичного замера изучаемого свойства. Такой подход вполне правомерен, поскольку размеры проб или сечения искусственных обнажений – скважин и горных выработок обычно неизмеримо малы по сравнению с изучаемыми геологическими объектами.

При статистическом моделировании предполагается, что выборочная совокупность отвечает требованиям массовости, однородности, случайности и независимости.

Условие массовости вызвано тем, что статистические закономерности проявляются лишь в массовых явлениях, поэтому объем выборочной совокупности должен быть достаточно большим. Эмпирическим путем установлено, что надежность статистических оценок резко снижается при уменьшении объема выборки в диапазоне от 60 до 30–20 значений, а при меньшем количестве наблюдений применять статистические методы в большинстве случаев вообще не имеет смысла. При проведении геологических, геохимических и геофизических съемок количество наблюдений, как правило, велико и условие массовости соблюдается. Однако, в процессе разведки месторождений полезных ископаемых, когда для каждого наблюдения обычно требуется проходка специальной горной выработки или скважины, геологу часто приходится иметь дело с малыми выборками. Это вызывает определенные трудности, так как свойства многих статистических оценок в данных условиях изучены недостаточно.

В связи с этим вопрос о минимально допустимом объеме выборки В дальнейшем будет рассматриваться применительно к решению отдельных конкретных задач.

Условие однородности заключается в том, что выборочная совокупность должна состоять из наблюдений, принадлежащих одному объекту и выполненных одинаковым способом, то есть при постоянном размере проб и методе анализа или измерения. Нарушения этого условия могут быть связаны с ошибками при определении границ изучаемой геологической совокупности или техническими и организационными сложностями проведения исследований.

Границы геологической совокупности обычно задаются исходя из поставленной задачи до получения массовых результатов исследования. При этом предполагается, что все объекты, включенные в геологическую совокупность, аналогичны и внутренне однородны. Однако это предположение подтверждается не всегда. Схожие по качественным признакам объекты могут иногда существенно отличаться по количественным характеристикам. К тому же большинство реальных геологических образований имеет сложное внутреннее строение, обусловленное зональностью и наличием элементов неоднородности разного масштаба.

При обобщении результатов геологических исследований часто приходится иметь дело с данными, полученными в разные годы с помощью различных технических средств.

В связи с тем, что условие однородности в практике геологических исследований соблюдается далеко не всегда, применение статистических методов должно сопровождаться анализом возможных последствий за счет нарушения данного условия. Для этого необходимо учитывать характер решаемой геологической задачи, а в ряде случаев использовать также специальные методы для проверки гипотезы об однородности выборки.

Условие случайности предусматривает непредсказуемость результата единичного выборочного наблюдения. Сложность и изменчивость геологических объектов, как правило, исключают возможность точной оценки их свойств до проведения наблюдения. Поэтому элемент случайности присутствует во всех геологических исследованиях. Однако условие случайности строго выполняется лишь тогда, когда расположение мест отбора проб или проведения замеров изучаемого свойства вообще не будет каким-либо образом связано с величиной, характеризующей это свойство. В практике проведения геологоразведочных работ это обычно достигается за счет проведения наблюдений по равномерной сети, когда все места наблюдений намечаются заранее до проведения работ и в процессе их выполнения не корректируются. Однако при изучении геологических образований по естественным обнажениям это условие может нарушаться. Так, например, на территориях со слабо расчлененным рельефом естественные обнажения преимущественно располагаются в бортах речных долин, которые, в свою очередь, часто совпадают с разрывными нарушениями или выходами пород, наиболее легко поддающихся процессам эрозии. В то же время прочностные свойства пород связаны с их текстурными особенностями и минеральным составом. Поэтому статистическая обработка результатов петрографических исследований или испытаний их физико-механических свойств по образцам, отобранным только из естественных обнажений, может дать искаженное представление о свойствах пород изученной территории в целом.

Условие случайности может нарушаться за счет субъективности при проведении замеров или отборе проб. Если при отборе образцов из толщи гнейсов один исследователь будет отдавать предпочтение прослоям более светлой окраски, а другой – прослоям более темной окраски, то полученные ими выборки будут существенно отличаться по среднему минеральному составу как друг от друга, так и от истинного среднего состава изучаемой толщи.

В процессе проведения геологоразведочных работ часто возникает необходимость в сгущении сети наблюдений на наиболее интересных или перспективных участках. Свойства геологических объектов в пределах этих участков и на всей остальной изучаемой территории могут существенно отличаться. Поэтому при статистической обработке данных для соблюдения условия случайности результаты наблюдений по участку детализации должны быть выделены в самостоятельную выборочную совокупность.

Условие независимости предполагает, что результаты каждого наблюдения не зависят от результатов предыдущих и последующих наблюдений, а при проведении наблюдений на площади или в объеме результаты не зависят от координат пространства. Для большинства геологических процессов и образований это условие не соблюдается. В изменчивости свойств геологических образований в пространстве и параметров геологических процессов во времени обычно наблюдаются определенные закономерности. Ввиду этого область применения статистических моделей ограничена объектами, для которых характерно отсутствие каких-либо закономерностей изменения в пространстве или во времени, или задачами, при решении которых эти закономерности можно не учитывать.

В геологической практике одномерные статистические модели используются для решения двух типов задач: оценки средних параметров геологических объектов и статистической проверки гипотез.

ПРОСТЕЙШИЕ ПРЕОБРАЗОВАНИЯ КОЛИЧЕСТВЕННОЙ ГЕОЛОГИЧЕСКОЙ ИНФОРМАЦИИ

В связи с возможными отклонениями условий изучения геологических объектов от строгих требований, предъявляемых к статистическому эксперименту, статистический анализ геологических данных целесообразно разделять на два этапа – разведочный и подтверждающий.

Цель первого этапа – преобразование наблюдаемых данных в более компактную и наглядную форму, позволяющую выявить имеющиеся в них закономерности. Это дает возможность более обоснованно подходить к выбору традиционных статистических методов решения геологических задач на втором этапе.

На первом этапе целесообразно применять методы, свободные от каких-либо априорных допущений относительно свойств выборочной совокупности и не требующие трудоемких расчетов. Предпочтение следует отдавать методам, где числовая информация преобразуется в графическую. Как отмечает Дж. Тьюки, график часто «вынуждает» нас заметить то, что мы совсем не ожидали увидеть.

Некоторые преобразования такого типа рассмотрим на ПРИМЕРЕ I.1.

ПРИМЕР I.1

Для определения петрографического типа пород из горизонта неогеновых лав отобрано и проанализировано на содержание SiO₂ 30 проб (табл. I.1). Содержание SiO₂ в отдельных пробах меняется от 56,6 (андезитобазальт) до 73,2% (риолит), что не позволяет оценить состав лав горизонта в целом по единичному наблюдению. Для получения усредненных характеристик приведенные в табл. I.1 данные необходимо каким-то способом преобразовать. Нетрудно заметить, что содержания SiO₂ по некоторым пробам близки и различаются лишь на десятые доли процента. Это позволяет заменить таблицу числовой диаграммой, которую американский статистик Дж. Тьюки образно назвал «стеблем с листьями». При построении диаграммы, часто повторяющиеся части чисел, в данном случае целые проценты содержаний SiO₂, записываются в порядке возрастания в виде вертикального столбца («стебля»), а оставшиеся части, в нашем примере десятые доли процента, записываются около соответствующей начальной части в горизонтальную строчку («листья»). Такая запись более компактна, наглядна, позволяет оценить частоту встречаемости значений в разных диапазонах, а также легко найти некоторые важные характеристики совокупности выборочных данных.

Таблица I.1. Содержание SiO₂ (в %) в неогеновых лавах

№ пробы	SiO2	№ пробы	SiO2	№ пробы	SiO2	№ пробы	SiO2
1	59,5	9	73,2	17	69,3	24	61,1
2	66,8	10	64,6	18	64,6	25	63,8
3	60,5	11	62,9	19	67,8	26	67,5
4	63,7	12	62,4	20	56,6	27	65,3
5	72,5	13	71,6	21	71,4	28	69,9
6	69,2	14	65,8	22	67,7	29	73,2
7	61,2	15	63,1	23	63,6	30	60,7
8	66,3	16	61,2

По рис. I.1, а легко определить, что из 30 проб по содержанию SiO₂ одна соответствует андезитобазальту, шесть – андезиту, две – андезит-дациту, тринадцать – дациту, три – риолит-дациту и пять – риолиту. Следовательно, определения, соответствующие дациту, явно преобладают. По числовой диаграмме легко находится также центр распределения – медиана. Для этого с любого конца «стебля» нужно отсчитать количество чисел («листьев»), равное половине общего количества замеров изучаемого свойства. В данном примере количество проб четное, поэтому центр распределения попадает в интервал между значениями 64,6 и 65,3%, то есть соответствует примерно 65%, что отвечает содержанию SiO₂ в даците. Таким образом, по числовой диаграмме можно сделать вывод о том, что средний состав лав изученного горизонта соответствует дациту.

Рис. I.1. Изображение содержаний SiO₂ (в %) в неогеновых лавах: а—числовая диаграмма «стебель с листьями»; б—схематическая диаграмма «ящик с усами»

Основные особенности числовых массивов могут быть также отображены на схематической диаграмме, названной Дж. Тьюки «ящиком с усами». На эти диаграммы в определенном масштабе выносятся минимальные и максимальные значения признака, медиана и так называемые «сгибы» – середины распределений в интервалах от медианы до минимального и максимального значения. Положение «сгибов» определяется по числовой диаграмме путем отсчета от медианы в сторону больших и меньших значений количества «листьев», равного 1/4 от их общего количества. Интервал между сгибами изображается в виде прямоугольника («ящика»), а интервалы от сгибов до максимального и минимального значения – в виде прямых линий («усов»). Иногда единичные значения на числовой диаграмме отделены от основной совокупности значительными интервалами – участками «стебля» без «листьев». Такие интервалы на схематической диаграмме целесообразно показывать пунктиром. По длине «ящика» и «усов» можно судить о характере разброса данных относительно медианы, оценивать степень асимметричности распределения, выявлять резкие отклонения по отдельным замерам от общей совокупности, оценивать однородность числового массива.

В приведенном примере в «ящик» попадают все определения, соответствующие дациту, а пробы с содержанием SiO₂, характерным для других пород, приходятся на «усы» (рис. I.1, б). При этом проба № 20, где содержание SiO₂ соответствует андезитобазальту, может рассматриваться как резкое отклонение, нетипичное для горизонта в целом.

Визуальное сравнение числовых и схематических диаграмм, построенных для нескольких геологических объектов, нередко позволяет произвести их предварительную группировку по принципу близости средних значений и степени изменчивости изучаемых свойств, а также выявить отличительные индивидуальные особенности каждого объекта.

Требуется

1)определить средний состав лав изученного горизонта методом построения диаграммы «стебель с листьями»;

2) определить средний состав лав;

3) определить преобладающий состав для большинства проб;

4) определить разброс значений.

Указание

Построение числовой диаграммы «стебель с листьями» удобно осуществить с помощью электронных таблиц Excel.

Задача решается с использованием процедур программы Statistica построением схематической диаграммы «ящик с усами», а затем путем анализа полученной графической информации.

Решение

1. Открыть электронные таблицы Excel. Ввести в столбец A порядковые номера проб (№ пробы). В столбец B – содержание (в %) SiO₂ в неогеновых лавах по табл. I.1. В ячейку A31 – формулу =СЧЕТ(A1:A30), в ячейку B31 – формулу =МАКС(B1:B30), в ячейку B32 – формулу =МИН(B1:B30) – см. рис. I.2.

Рис. I.2. Использование электронных таблиц Excel для построения диаграммы «стебель с листьями»

По этим данным можно построить диаграмму «стебель с усами». В диапазон D7:D24 через меню Правка/Заполнить/Прогрессия… ввести числовой ряд от 56 до 73 (см. рис. I.2). А оставшиеся части, в нашем примере десятые доли процента, записать около соответствующей начальной части в горизонтальную строчку («листья») – столбцы E – H. Для контроля общего числа проб в ячейку E25 ввести формулу =СЧЕТ(E7:E24), эту формулу методом автозаполнения скопировать в ячейки F25, G25, H25. В ячейку I25 кнопкой Автосумма подсчитать общее количество проб – 30. Заливка цветом столбца B была использована для самоконтроля при вводе десятых долей процента при построении диаграммы «стебель с листьями». Запись наглядна, позволяет оценить частоту встречаемости значений в разных диапазонах.

2. В системе STATISTICA создается файл данных, используя числовую табл. I.1.

В системе STATISTICA данные организованы в виде наблюдений и переменных. Наблюдения можно рассматривать как эквивалент записей в программе управления базами данных (или строк электронной таблицы), а переменные - как эквивалент полей (столбцов электронной таблицы). Каждое наблюдение состоит из набора значений переменной.

Через меню Data/Cases/Add… вызвать диалоговое окно Add Cases (см. рис. I.3) добавить 20 записей к существующим по умолчанию десяти. Через меню Data/Vars/Delete… удалить столбцы, начиная со второго по десятый (см. рис. I.4). Далее привести документ к виду, показанному на рис. I.5, заполнив столбец данными табл. I.1. Сохранить файл.

Рис. I.3. Заполнение диалогового окна Add Cases

Рис. I.4. Заполнение диалогового окна Delete Variables

Рис. I.5. Заполнение столбца Var1 данными табл. I.1

3. В меню программы Statistica выбирается Basic Statistics/Tables и подпункт Descriptive statistics – расчет описательных статистик (рис. I.6). В диалоговом окне Descriptive Statistics нажимается кнопка Box & whisker plot for all variables – график «ящик с усами» (рис. I.7). В появившемся новом окне вводится имя переменной для исследования (рис. I.8). В результате появится необходимая диаграмма (рис. I.9).

Рис. I.6. Выбор подпункта Descriptive statistics

Рис. I.7. Выбор кнопки Box & whisker plot for all variables

Рис. I.8. Ввод имени переменной для исследования

Рис. I.9. Окончательный вид диаграммы «ящик с усами»

4. Для определения петрографического типа пород можно использовать классификацию магматических пород Ф.Ю. Левинсон-Лессинга: к средним породам (группа диорита–андезита) относятся породы с содержанием SiO₂ от 52 до 65%, к кислым породам (группа гранита–риолита) относятся породы с содержанием SiO₂ больше 65%. (По классификации Левинсон-Лессинга существуют две магмы – кислая и основная).

Примечание

В электронных таблицах Excel так же можно построить диаграмму «ящик с усами». В ячейке D31 определена медиана с помощью формулы =МЕДИАНА(B1:B30). Руководствуясь описанием построения этой диаграммы в настоящей работе и рис. I.10, постройте диаграмму «ящик с усами» в электронных таблицах Excel. Цветом на рис. I.10 выделены «листья» диаграммы, которые следует отсчитать от медианы вверх и вниз по восемь «листьев».

Рис. I.10. Построение диаграммы «ящик с усами» в Excel

Границы ящика можно найти с помощью функций Excel =НАИБОЛЬШИЙ(массив;k) и =НАИМЕНЬШИЙ(массив;k). Для этого скопируем ячейки B1:B30 на лист 2 в столбец B, выделим диапазон скопированных ячеек и отсортируем его с помощью пункта меню Данные/Сортировка…, указав в пределах указанного диапазона – по возрастанию, после чего, учитывая, что всего 30 проб – четное число, в ячейку C15 введем формулу =НАИБОЛЬШИЙ(B1:B15;8), а в ячейку C16 – формулу =НАИМЕНЬШИЙ(B16:B30;8). Тогда в ячейках C15 и C16 соответственно отобразятся числа 62,4 и 69,2 – границы ящика (рис. I.11).

Рис. I.11. Построение границ ящика диаграммы «ящик с усами»

Сравнить диаграммы на рис. I.9 и рис. I.10 и сделать выводы об области применимости пакетов Excel и STATISTICA при построении диаграммы «ящик с усами».

ЗАДАЧА I.1

На месторождении редких металлов с целью количественного описания морфологии рудных тел были замерены их площади по разведочным разрезам, ориентированным вкрест простирания рудовмещающих структур. По результатам замеров, приведенным в табл. I.2, можно заключить, что для всех изученных рудных тел характерна сильная изменчивость данного параметра. Это затрудняет сравнение рудных тел непосредственно по табличным данным.

Таблица I.2. Площади рудных тел в поперечных разрезах (в м²)

№ разреза	№ рудного тела				№ разреза	№ рудного тела
	525	518	501	509		525	518	501	509
1	232	119	137	25	14		451	260	77
2	293	120	177	56	15		627	68	195
3	87	130	98	101	16		597	254	234
4	121	417	25	634	17		726	211	219
5	422	355	115	340	18		686	254	75
6	1580	198	360	195	19		683	82	43
7	835	567	195	158	20		525	100
8	204	504	493	24	21		605	9
9	218	574	487	210	22		1042	30
10	243	404	379	50	23		504
11	146	502	247	228	24		648
12	49	697	116	335	25		220
13	174	579	629	153

Рис. I.12. Схематические диаграммы площадей рудных тел по разрезам

В то же время числовые и схематические диаграммы (табл. I.3, рис. I.12) позволяют увидеть некоторые интересные особенности:

• рудные тела 501 и 509 весьма схожи как по среднему значению площади в поперечном сечении, так и по степени изменчивости этого параметра;

• рудное тело 525 отличается от рудных тел 501 и 509 лишь наличием резких увеличений площади по единичным разрезам;

• рудное тело 525 явно отличается от остальных рудных тел большей площадью в поперечных сечениях.

Таблица I.3. Числовые диаграммы площадей рудных тел в поперечных разрезах

Сотни, м2	м2
0	87,49		98, 25, 68, 82, 09,30	25, 56, 24, 50, 77, 75, 43
1	21,46,74	19, 20, 30, 98	37, 77, 15,95, 16,00	01,95,58,53, 95
2	32, 93, 04, 18,43	20	47,60,54, 11, 54	10, 28, 34, 19
3		55	60,79	40 35
4	22	17, 04, 51	93,87
5		67, 04, 74, 02, 79, 97, 25, 04
6		97, 27, 86, 83, 05, 48	29	34
7		26
8		35
9
10		42
11
12
13
14
15	80
№ рудного тела	525	518	501	509

Требуется

1) определить средние значения площадей рудных тел в поперечных разрезах;

2) определить преобладающие значения площадей рудных тел в поперечных разрезах;

3) определить разброс значений.

Указание

Построение числовых диаграмм «стебель с листьями» и «ящик с усами» можно осуществить с помощью электронных таблиц Excel. Например, для рудного тела № 518 вид диаграмм представлен на рис. I.13.

Рис. I.13. Построение диаграмм «стебель с листьями» и «ящик с усами» в Excel

Задача может быть решена с использованием процедур программы Statistica построением схематической диаграммы «ящик с усами». Для каждого рудного тела данные следует заносить в свой столбец (создать 4 столбца и 25 строк). В меню программы Statistica выбрать Basic Statistics/Tables и его подпункт «Descriptive statistics». В диалоговом окне Descriptive Statistics нажать кнопку Box & whisker plot for all variables. В появившемся новом окне ввести имена переменных для исследования. Здесь нужно выбрать пункт Select All. Таким образом, на один график будут помещены диаграммы, характеризующие разные рудные тела. Результат представлен на рис. I.14.

Рис. I.14. Построение диаграммы «ящик с усами» в Statistica

ЗАДАЧА I.2

Месторождение силикатного никеля приурочено к латеритной коре выветривания ультрамафитов. По минеральному составу и текстурным особенностям в вертикальном разрезе коры выветривания сверху вниз выделяются шесть зон:

Зона 1. Железистых стяжений;

Зона 2. Бесструктурных охр;

Зона 3. Конечных структурных охр;

Зона 4. Структурных полуохр;

Зона 5. Выщелоченных материнских пород;

Зона 6. Дезинтегрированных материнских пород.

Для изучения химического состава коры выветривания и поведения различных химических элементов в процессе корообразования на одном из участков месторождения из каждой зоны были отобраны пробы, по которым выполнены анализы на Fe₂O₃, NiO, CoO, SiO₂, MgO, Al₂O₃, Cr₂O₃ (табл. I.4 – I.10).

Требуется

1) выявить отличительные особенности химического состава различных зон;

2) установить характер поведения различных химических элементов в процессе корообразования;

3) выделить ассоциации химических элементов, сходных по характеру поведения в процессе корообразования.

Задание можно выполнять бригадами.

Указание

Для выявления различий химического состава коры выветривания разных зон необходимо результаты анализов на каждый химический элемент представить в виде, удобном для сравнения. Исходные данные можно преобразовать в графические диаграммы «ящик с усами». Задача решается с использованием процедур программы Statistica, а затем путем анализа полученной графической информации.

1. Создается файл данных, используя одну из числовых таблиц I.4 – I.10.

2. В меню программы Statistica выбирается Basic Statistics/Tables и его подпункт «Descriptive statistics». В диалоговом окне Descriptive Statistics нажимается кнопка Box & whisker plot for all variables. В появившемся новом окне вводятся имена переменных для исследования. Здесь нужно выбрать пункт Select All. Таким образом, на один график будут помещены диаграммы, характеризующие разные зоны (рис. I.15).

3. Диаграммы можно использовать для анализа поведения химических элементов в процессе породообразования. Уменьшение значения медианы при переходе от нижней зоны к верхней указывает на вынос данного элемента, а увеличение – на его малую подвижность и накопление в коре выветривания. Увеличение размаха варьирования (длины «усов») без заметного смещения медианы указывает на локальное перераспределение данного элемента в пределах зоны.

Таблица I.4. Содержание Fe₂O₃ в различных зонах коры выветривания

№ проб	Зона 1	Зона 2	Зона 3	Зона 4	Зона 5	Зона 6
1	56,26	68,78	65,90	52,08	13,11	5,95
2	57,20	71,21	69,70	54,31	14,05	5,79
3	61,06	63,49	61,01	48,85	20,28	6,24
4	58,63	65,49	67,72	33,07	21,37	5,09
5		70,04	59,60	32,08
6		70,13	61,32	33,41
7		70,38	61,92	28,18
8				28,58
9				32,17
10				40,19
11				27,51
12				29,83

Таблица I.5. Содержание NiO в различных зонах коры выветривания

№ проб	Зона 1	Зона 2	Зона 3	Зона 4	Зона 5	Зона 6
1	0,35	1,65	1,36	1,23	0,42	0,27
2	0,38	1,36	0,90	2,59	1,33	0,41
3	0,50	1,06	1,35	3,63	1,22	0,44
4	0,29	1,44	1,30	2,32	1,12	0,32
5		1,35	0,66	1,17
6		1,12	1,65	1,41
7		1,10	2,69	1,16
8				2,58
9				2,09
10				3,28
11				1,50
12				2,55

Таблица I.6. Содержание CoO в различных зонах коры выветривания

№ проб	Зона 1	Зона 2	Зона 3	Зона 4	Зона 5	Зона 6
1	0,089	0,200	0,197	0,206	0,019	0,090
2	0,073	0,046	0,056	0,213	0,027	0,013
3	0,013	0,143	0,320	0,078	0,037	0,015
4	0,027	0,255	0,085	0,108	0,039	0,013
5		0,028	0,039	0,091
6		0,016	0,076	0,104
7		0,095		0,067
8				0,069
9				0,059
10				0,080
11				0,045
12				0,070

Таблица I.7. Содержание SiO₂ в различных зонах коры выветривания

№ проб	Зона 1	Зона 2	Зона 3	Зона 4	Зона 5	Зона 6
1	6,73	2,30	3,98	12,48	36,00	37,52
2	7,91	3,27	2,32	13,26	38,77	38,96
3	4,40	7,92	6,32	18,99	33,44	41,30
4	5,28	4,21	2,02	26,19	34,15	38,21
5		1,97	6,37	24,20
6		3,09	10,89	26,51
7		2,00	11,26	27,04
8				28,36
9				26,10
10				21,94
11				37,86
12				31,12

Таблица I.8. Содержание MgO в различных зонах коры выветривания

№ проб	Зона 1	Зона 2	Зона 3	Зона 4	Зона 5	Зона 6
1	2,85	0,75	1,00	8,78	32,66	38,96
2	0,95	1,05	0,50	8,26	28,54	38,22
3	0,80	1,25	2,60	7,72	27,69	37,28
4	1,10	1,00	0,85	17,64	26,74	39,18
5		0,75	2,85	18,25
6		1,75	3,15	18,35
7		1,05	2,70	19,68
8				20,58
9				19,54
10				15,20
11				12,92
12				18,25

Таблица I.9. Содержание Al₂O₃ в различных зонах коры выветривания

№ проб	Зона 1	Зона 2	Зона 3	Зона 4	Зона 5	Зона 6
1	14,45	10,62	9,95	7,91	1,88	0,92
2	15,99	6,26	6,53	5,52	2,16	0,66
3	14,14	10,05	6,94	4,32	2,51	0,66
4	14,17	10,35	6,55	4,08	1,77	0,39
5		7,63	10,88	8,08
6		6,81	6,43	4,18
7		7,55	4,54	7,13
8				3,42
9				3,98
10				3,14
11				5,10
12				2,63

Таблица I.10. Содержание Cr₂O₃ в различных зонах коры выветривания

№ проб	Зона 1	Зона 2	Зона 3	Зона 4	Зона 5	Зона 6
1	2,70	2,36	2,32	2,49	1,22	0,40
2	2,24	2,97	2,76	2,42	0,49	0,36
3	2,80	2,34	2,03	0,24	0,94	0,28
4	3,28	2,19	2,62	1,79	1,12	0,28
5		3,53	3,11	1,58
6		2,81	2,31	1,81
7		2,69	2,06	1,72
8				1,28
9				1,68
10				1,88
11				1,23
12				1,50

Рис. I.15. Построение по табл. I.4 диаграммы «ящик с усами» в Statistica

ЛАБОРАТОРНАЯ РАБОТА № II. ОДНОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ, ИСПОЛЬЗУЕМЫЕ В ГЕОЛОГИИ. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ. ИНТЕРВАЛЬНЫЕ ОЦЕНКИ СВОЙСТВ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ

На рис. II.1 изображены гистограмма и кумулята распределения SiO₂ в неогеновых лавах (см. ЛАБОРАТОРНУЮ РАБОТУ № I. ПРИМЕР I.1). Для построения графиков распределений выборочные данные первоначально целесообразно представить в виде числовой диаграммы «стебель с листьями». Это позволяет правильно выбрать длину классового интервала и быстро подсчитать количество значений в каждом классе (табл. II.1).

Рис. II.1. Графики частотного распределения содержания SiO₂ в неогеновых лавах: а—гистограмма; б—кумулята

Таблица II.1. Частотное распределение содержаний SiO₂ в неогеновых лавах

Содержание SiO2		Класс, от – до	Частота	Частость, %	Накопленная частость, %
целые числа	десятые доли
56	6
57		56,0–58,9	1	3	3
58
59	5
60	5,7	59,0–61,9	6	20	23
61	2,2,1
62	9,4
63	7,1,6,8	62,0–64,9	8	27	50
64	6,6
65	8,3
66	8,3	65,0–67,9	7	23	73
67	8,7,5
68
69	2,3,9	68,0–70,9	3	10	83
70
71	6,4
72	5	71,0–73,9	5	17	100
73	2,2

ВЫБОРОЧНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

В Excel для построения выборочных функций распределения используются специальная функция ЧАСТОТА и процедура пакета анализа Гистограмма.

• Функция ЧАСТОТА вычисляет частоты появления случайной величины в интервалах значений и выводит их как массив цифр. Функция задается в качестве формулы массива. ЧАСТОТА(массив_данных; массив_карманов). Здесь:

• массив_данных – это массив или ссылка на множество данных, для которых вычисляются частоты.

• массив_карманов – это массив или ссылка на множество интервалов, в которые группируются значения аргумента массив_данных. Отметим, что количество элементов в возвращаемом массиве на единицу больше числа элементов в массив_карманов. Дополнительный элемент в возвращаемом массиве содержит количество значений, больших, чем максимальное значение в интервалах.

• Процедура Гистограмма используется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. Процедура выводит результаты в виде таблицы и гистограммы.

Параметры диалогового окна Гистограмма:

• во Входной диапазон вводится диапазон исследуемых данных;

• в поле Интервал карманов (необязательный параметр) может вводиться диапазон ячеек или необязательный набор граничных значений, определяющих выбранные интервалы (карманы). Эти значения должны быть введены в возрастающем порядке. В Excel вычисляется число попаданий данных между началом интервала и соседним большим по порядку. При этом включаются значения на нижней границе интервала и не включаются значения на верхней границе. Если диапазон карманов не был введен, то набор интервалов, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически;

• рабочее поле Выходной диапазон предназначено для ввода ссылки на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически;

• переключатель Интегральный процент позволяет установить режим генерации интегральных процентных отношений и включения в гистограмму графика интегральных процентов;

• переключатель Вывод графика позволяет установить режим автоматического создания встроенной диаграммы на листе, содержащем выходной диапазон.

ПРИМЕР II.1

Требуется

Построить эмпирическое распределение содержания SiO₂ в неогеновых лавах для выборки (см. табл. I.1.).

Решение

1. В ячейку А1 введите заголовок Наблюдения, а в диапазон А2:A31 – значения (в %) содержания SiO₂ в неогеновых лавах. В ячейке A32 подсчитайте максимальное значение, в ячейке A33 – минимальное значение.

2. Выберите ширину интервала 1%. Тогда при крайних значениях 56% и 74% получится 18 интервалов. В ячейку D1 введите название Границы интервалов. В диапазон D2:D20 введите через меню Правка/Заполнить/Прогрессия… числовой ряд от 56 до 74 (56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74).

3. Введите заголовки создаваемой таблицы: в ячейки E1 – Абсолютные частоты, в ячейки F1 – Относительные частоты, в ячейки G1 – Накопленные частоты.

4. Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек E2:E20 (используемая функция ЧАСТОТА задается в виде формулы массива). С панели инструментов Стандартная вызовите Мастер функций (кнопка f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ЧАСТОТА, после чего нажмите кнопку OK. Появившееся диалоговое окно ЧАСТОТА необходимо за серое поле мышью отодвинуть вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши в рабочее поле Массив_данных введите диапазон данных наблюдений (А2:A31). В рабочее поле Двоичный_массив мышью введите диапазон интервалов (D2:D20). Последовательно нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце E2:E20 появится массив абсолютных частот.

5. В ячейке E21 найдите общее количество наблюдений. Табличный курсор установите в ячейку E21. На панели инструментов Стандартная нажмите кнопку Автосумма. Убедитесь, что диапазон суммирования указан правильно (E2: E20), и нажмите клавишу Enter. В ячейке E21 появится число 30.

6. Заполните столбец относительных частот. В ячейку F2 введите формулу для вычисления относительной частоты: =E2/E$21. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон F3:F20. Получите массив относительных частот.

7. Заполните столбец накопленных частот. В ячейку G2 скопируйте значение относительной частоты из ячейки F2. В ячейку G3 введите формулу: =G2+F3. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон G3:G20. Получите массив накопленных частот.

8. В результате, после форматирования получим таблицу, представленную на рис. II.2.

9. Постройте диаграмму относительных и накопленных частот. Щелчком указателя мыши по кнопке на панели инструментов вызовите Мастер диаграмм. В появившемся диалоговом окне выберите вкладку Нестандартные и тип диаграммы График/гистограмма2. После нажатия кнопки Далее укажите диапазон данных – F1:G20 (с помощью мыши). Проверьте положение переключателя Ряды в: столбцах. Выберите вкладку Ряд и с помощью мыши введите в рабочее поле Подписи оси Х диапазон подписей оси Х: D2:D20. Нажав кнопку Далее, введите названия осей Х и Y в рабочее поле. Ось Х (категорий) – Наблюдения, Ось Y (значений) – Относ.частота, Вторая ось Y (значений) – Накоплен.частота. Нажмите кнопку Готово.

Рис. II.2. Результат вычислений относительных и накопленных частот

Диаграмма будет иметь такой вид, как на рис. II.3.

Рис. II.3. Диаграмма относительных и накопленных частот

ПРИМЕР II.2

Требуется

Для данных из предыдущего примера построить эмпирические распределения, воспользовавшись процедурой Гистограмма.

Решение

1. В ячейку А1 введите заголовок Наблюдения, а в диапазон в диапазон А2:A31 – значения содержания SiO₂ в неогеновых лавах.

2. Для вызова процедуры Гистограмма выберите из меню Сервис подпункт Анализ данных и в открывшемся окне в поле Инструменты анализа укажите процедуру Гистограмма.

3. В появившемся окне Гистограмма заполните рабочие поля:

• во Входной диапазон введите диапазон исследуемых данных (А2:A31);

• в Выходной диапазон – ссылку на левую верхнюю ячейку выходного диапазона (C2). Установите переключатели в положение Интегральный процент и Вывод графика;

После этого нажмите кнопку OK. В результате появляется таблица и диаграмма, представленные на рис. II.4.

Рис. II.4. Таблица и диаграмма

Как видно, эта диаграмма несколько отличается от диаграммы предыдущего примера. Это объясняется тем, что диапазон карманов не был введен. Количество и границы интервалов определялись в процедуре Гистограмма автоматически. Если бы в рабочее поле Интервал карманов был бы введен диапазон ячеек, определяющих выбранные интервалы, как в предыдущем примере (56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74), то полученная диаграмма была бы идентична предыдущей.

ОПРЕДЕЛЕНИЕ ОСНОВНЫХ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК

В результате наблюдений или эксперимента получаются наборы данных, называемые выборками. Для проведения их анализа данные подвергаются статистической обработке. Первое, что всегда делается при обработке данных, это вычисление элементарных статистических характеристик выборок (как минимум: среднего, среднеквадратичного отклонения, ошибки среднего) по каждому параметру и по каждой группе. Полезно также вычислить эти характеристики для объединения родственных групп и суммарно по всем данным.

ИСПОЛЬЗОВАНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ

В мастере функций Excel имеется ряд специальных функции, предназначенных для вычисления выборочных характеристик. Прежде всего, это функции, характеризующие центр распределения.

• Функция СРЗНАЧ вычисляет среднее арифметическое из нескольких массивов (аргументов) чисел. Аргументы число 1, число2, ... – это от 1 до 30 массивов, для которых вычисляется среднее. Например, если ячейки А1:А7 содержат числа 10, 14, 5, 6, 10, 12 и 13, то средним арифметическим СРЗНАЧ(A1:А7) является 10.

• Функция МЕДИАНА позволяет получать медиану заданной выборки. Медиана – это элемент выборки, число элементов выборки со значениями больше которого и меньше которого равно. Например, МЕДИАНА(10;14;5;6;10;12;13) равняется 10.

• Функция МОДА вычисляет наиболее часто встречающееся значение в выборке. Например, МОДА(10;14;5;6;10;12;13) равняется 10.

К специальным функциям, вычисляющим выборочные характеристики, характеризующие рассеяние вариант, относятся ДИСП, СТАНДОТКЛОН.

• Функция ДИСП позволяет оценить дисперсию по выборочным данным. Например, ДИСП(10;14;5;6:10;12;13) равняется 11,667.

• Функция СТАНДОТКЛОН вычисляет стандартное отклонение. Например, СТАНДОТКЛОН(10;14;5;6;10;12;13) равняется 3,416.

Форму эмпирического распределения позволяют оценить специальные функции ЭКСЦЕСС и СКОС.

• Функция ЭКСЦЕСС вычисляет оценку эксцесса по выборочным данным. Например, ЭКСЦЕСС(10;14;5;6;10;12;13) равняется -1,169.

• Функция СКОС позволяет оценить асимметрию выборочного распределения. Например, СКОС(10;14;5;6;10;12;13) равняется -0,527.

Серия функций отличается наличием или отсутствием на конце названия буквы А (начиная с Excel 7.0). Если буква А отсутствует, то из блока для расчета выбираются только числовые значения, а текстовые игнорируются. Если имя итоговой функции заканчивается на букву А, то считается, что текстовая строка имеет нулевое значение (если в диапазон входит слово ИСТИНА, то оно считается эквивалентным значению 1).

Помимо среднего значения, важной характеристикой набора точек является разброс точек вокруг среднего значения. Для измерения степени разброса служат дисперсия и квадратный корень из дисперсии – среднеквадратичное отклонение. Но здесь есть одна тонкость. В математической статистике различают генеральную совокупность наблюдений (все возможные наблюдения) и выборку из генеральной совокупности. Для расчета дисперсии выборки и дисперсии генеральной совокупности используются разные формулы. Формула для дисперсии выборки реализована в функции ДИСП, а для расчета дисперсии генеральной совокупности используется несколько отличная формула – она реализована в функции ДИСПР (рис. II.5).

	A	B	C	D
1	7		3	=СЧЕТ($A1$:$A$4)
2	1		4	=СЧЕТЗ($A1$:$A$4)
3	куб		1	=МИН($A1$:$A$4)
4	4		0	=МИНА($A1$:$A$4)
5			7	=МАКС($A1$:$A$4)
6			7	=МАКСА($A1$:$A$4)
7			4	=СРЗНАЧ($A1$:$A$4)
8			3	=СРЗНАЧА($A1$:$A$4)
9			9	=ДИСП($A1$:$A$4)
10			10	=ДИСПА($A1$:$A$4)
11			6	=ДИСПР($A1$:$A$4)
12			7,5	=ДИСПРА($A1$:$A$4)
13			3	=СТАНДОТКЛОН($A1$:$A$4)
14			3,162	=СТАНДОТКЛОНА($A1$:$A$4)
15			2,449	=СТАНДОТКЛОНП($A1$:$A$4)
16			2,738	=СТАНДОТКЛОНПА($A1$:$A$4)
17			2	=СРОТКЛ($A1$:$A$4)

Рис. II.5. Фрагмент таблицы для расчета функций

Сами формулы можно найти в Справке, а также в любом курсе математической статистики. Для больших размеров генеральной совокупности и выборки значения, вычисленные по обеим формулам, различаются незначительно. Чаще всего применяется ДИСП, и поэтому функция СТАНДОТКЛОН – это квадратный корень из ДИСП. Функция СТАНДОТКЛОНП – квадратный корень из дисперсии генеральной совокупности – ДИСПР. Окончание А в этих функциях означает, что в расчет включаются текстовые величины, которые полагаются равными нулю.

Для измерения разброса изредка применяется функция СРОТКЛ, которая вычисляется как среднее арифметическое абсолютных величин отклонений от среднего значения.

ПРИМЕР II.3

Требуется

Используя исходные данные ПРИМЕРА II.1 настоящей работы, найти характеристики распределения этих данных.

Решение

1. В ячейку А1 введите заголовок Наблюдения, а в диапазон А2:A31 – значения содержания SiO₂ в неогеновых лавах. Отметим, что рассматриваемая группа данных со статистической точки зрения являются выборкой.

2. При статистическом анализе прежде всего необходимо определить характеристики выборки, и важнейшей характеристикой является среднее значение. Для определения среднего значения в контрольной группе необходимо установить табличный курсор в свободную ячейку (А34). На панели инструментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию СРЗНАЧ, после чего нажмите кнопку OK. Появившееся диалоговое окно СРЗНАЧ за серое поле мышью отодвиньте вправо на 1-2 см отданных (при нажатой левой кнопке). Указателем мыши введите диапазон данных группы для определения среднего значения (А2:А31). Нажмите кнопку OK. В ячейке А34 появится среднее значение выборки – 65,5667.

3. Следующей по важности характеристикой выборки является мера разброса элементов выборки от среднего значения. Такой мерой является среднее квадратичное или стандартное отклонение. Для определения стандартного отклонения в контрольной группе необходимо установить табличный курсор в свободную ячейку (А35). На панели инструментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию СТАНДОТКЛОНП, после чего нажмите кнопку OK. Появившееся диалоговое окно СТАНДОТКЛОНП за серое поле мышью отодвиньте вправо на 1-2 см отданных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы для определения стандартного отклонения (А2:А31). Нажмите кнопку OK. В ячейке А35 появится стандартное отклонение выборки – 4,307. В ячейке B35 по формуле =3*СТАНДОТКЛОНП(A2:A31) подсчитайте значение 3*σ: 12,922, где σ – стандартное отклонение. Существует правило, согласно которому для распределения близкого к нормальному данные должны лежать в диапазоне (в примере 65,567±12,922). Это правило называется правилом трех сигм. Сущность этого правила: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения [6]. Согласно этому правилу, в пределах находится 99,7% всех вариант.

4. В свободных ячейках A36 – A40 рассчитайте выборочную дисперсию, медиану, моду, асимметрию, эксцесс.

ИСПОЛЬЗОВАНИЕ ИНСТРУМЕНТОВ ПАКЕТА АНАЛИЗА

В пакете Excel помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками и углубленного анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.

Для установки раздела Анализ данных в пакете Excel сделайте следующее:

• в меню Сервис выберите команду Надстройки;

• в появившемся списке установите флажок Пакет анализа.

Ввод данных. Исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. При создании таблицы Excel информация вводится в отдельные ячейки. Совокупность ячеек, содержащих анализируемые данные, называется входным диапазоном.

Последовательность обработки данных. Для использования статистического пакета анализа данных необходимо:

• указать курсором мыши на пункт меню Сервис и щелкнуть левой кнопкой мыши;

• в раскрывающемся списке выбрать команду Анализ данных (если команда Анализ данных отсутствует в меню Сервис, то необходимо установить в Excel пакет анализа данных);

• выбрать необходимую строку в появившемся списке Инструменты анализа;

• ввести входной и выходной диапазоны и выбрать необходимые параметры.

Нахождение основных выборочных характеристик. Для определения характеристик выборки используется процедура Описательная статистика. Процедура позволяет получить статистический отчет, содержащий информацию о центральной тенденции и изменчивости входных данных. Для выполнения процедуры необходимо:

• выполнить команду Сервис/Анализ данных;

• в появившемся списке Инструменты анализа выбрать строку Описательная статистика и нажать кнопку OK;

• в появившемся диалоговом окне указать входной диапазон, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

• указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной диапазон (навести указатель мыши и щелкнуть левой клавишей), далее навести указатель мыши в поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши;

• в разделе Группировка переключатель установить в положение по столбцам;

• установить флажок в поле Итоговая статистика;

• нажать кнопку OK.

В результате анализа в указанном выходном диапазоне для каждого столбца данных выводятся следующие статистические характеристики: среднее, стандартная ошибка (среднего), медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумма, счет, наибольшее, наименьшее, уровень надежности.

ПРИМЕР II.4

Требуется

По данным ПРИМЕРА II.1 настоящей работы, определить основные статистические характеристики распределения этих данных, используя Пакет анализа электронных таблиц Excel.

Решение

1. В ячейку А1 введите заголовок Наблюдения, а в диапазон в диапазон А2:A31 – значения содержания SiO₂ в неогеновых лавах.

2. Далее необходимо провести элементарную статистическую обработку Для этого, указав курсором мыши на пункт меню Сервис, выберите команду Анализ данных. Затем в появившемся списке Инструменты анализа выберите строку Описательная статистика.

3. В появившемся диалоговом окне в рабочем поле Входной интервал укажите входной диапазон – A1:A32. Активировав переключателем рабочее поле Выходной интервал, укажите выходной диапазон – ячейку C14. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в поле Итоговая статистика и флажок Метки в первой строке, чтобы вывести заголовок из ячейки A1, нажмите кнопку OK.

В результате анализа в указанном выходном диапазоне для столбца данных получим соответствующие результаты – см. рис. II.6. Если бы столбцов было несколько, то получили результаты для каждого столбца.

Все полученные характеристики были рассмотрены ранее в разделе «Выборочные характеристики», за исключением последних четырех:

• минимум – значение минимального элемента выборки;

• максимум – значение максимального элемента выборки;

• сумма – сумма значений всех элементов выборки;

• счет – количество элементов в выборке.

Среди этих характеристик наиболее важными являются показатели Среднее, Стандартная ошибка (среднего) и Стандартное отклонение.

Ошибка среднего (стандартная ошибка) рассчитывается как отношение выборочного стандартного отклонения (среднеквадратичного отклонения) к корню квадратному из числа наблюдений выборки.

Рис. II.6. Результаты работы инструмента Описательная статистика

ПРИМЕР II.5

Требуется

Используя исходные данные ПРИМЕРА II.1 настоящего учебного пособия, определить основные статистические характеристики распределения этих данных, построить график, кумулятивный график и гистограмму частот. Решение задач дескриптивной статистики следует осуществить в пакете STATISTICA.

Решение

В системе STATISTICA создается файл данных, используя числовую таблицу I.1. Через меню Data/Cases/Add… вызвать диалоговое окно Add Cases (см. рис. II.7) добавить 20 строк к существующим по умолчанию десяти. Через меню Data/Vars/Delete… удалить столбцы, начиная со второго по десятый (см. рис. II.8). Далее привести документ к виду, показанному на рис. II.9, заполнив столбцы данными табл. I.1. Сохранить файл.

Рис. II.7. Заполнение диалогового окна Add Cases

Рис. II.8. Заполнение диалогового окна Delete Variables

Рис. II.9. Заполнение столбца Var1 исходными данными

Первой задачей обработки является вычисление числовых характеристик выборки. В меню Statistics программы Statistica выбирается пункт Basic Statistics/Tables и далее раздел Descriptive statistics – расчет описательных статистик (рис. II.10). В диалоговом окне Descriptive Statistics выбирается вкладка Advanced, где отметим показатели, которые требуется вычислить (рис. II.11): Valid N (объем выборки), Mean (среднее), Sum (Сумма), Median (медиана), Mode (Мода), Standart Deviation (среднее квадратическое отклонение), Variance (дисперсия), Std.err.of mean (ошибка среднего), Minimum & maximum (минимум и максимум), Range (размах варьирования), Lower & upper quartiles (нижняя и верхняя четверть), Skewness (асимметрия), Std.err., Skewness (ошибка асимметрии), Kurtosis (эксцесс), Std.err., Kurtosis (ошибка эксцесса). Затем нажимается кнопка Variables (переменная) (рис. II.12). Укажите переменную Var 1. Нажмите одну из кнопок Summary (итог). Результаты расчета показаны на рис. II.13

Рис. II.10. Выбор подпункта Descriptive statistics

Рис. II.11. Выбор вкладки Advanced диалогового окна Descriptive statistics

Рис. II.12. Ввод имени переменной для исследования

Рис. II.13. Результаты расчета числовых характеристик выборки

Следующей задачей обработки является построение таблицы и графиков частот. В левом нижнем углу нажмите кнопку свернутого диалогового окна Descriptive statistics и вернитесь в диалоговое окно. Откройте вкладку Quick и нажмите на кнопку Frequency tables, в результате получите таблицу частот, представленную на рис. II.14. В первом столбце таблицы заданы интервалы для переменной, причем последняя строка содержит пропущенные (Missing) значения. Второй столбец содержит число попаданий переменной в интервалы (Count), третий столбец – кумулятивное число попаданий (Cumul. Count), четвертый и шестой столбцы – частоты в процентах соответственно для имеющихся в наличии (не пропущенных) наблюдений (Percent of Valid) и для всех наблюдений (% of Cases), пятый и седьмой столбцы – кумулятивные частоты в процентах, соответственно для имеющихся в наличии (не пропущенных) наблюдений (Cumul.% of Valid) и для всех наблюдений (Cumul.% of All).

Для построения графиков частот и кумулятивных частот выделите два столбца таблицы Percent of Valid и Cumul.% of Valid и выполните команду контекстного меню Graphs of Block Data/Line Plot: Entire Columns. В результате получите графики, представленные на рис. II.15.

Для построения гистограммы частот в левом нижнем углу нажмите кнопку свернутого диалогового окна Descriptive statistics и вернитесь в диалоговое окно. Откройте вкладку Quick и нажмите на кнопку Histograms (Гистограммы), получите гистограмму, представленную на рис. II.16. Кроме гистограммы частот на рисунке показана теоретическая кривая плотности распределения наблюдаемой случайной величины в случае нормального закона.

Рис. II.14. Таблица частот

Рис. II.15. Графики частот и кумулятивных частот

Рис. II.16. Гистограмма частот

ЗАДАЧА II.1

Характеристики положения и разброса угловых величин имеют некоторые специфические особенности. В этом нетрудно убедиться на следующем примере. В табл. II.2 и на рис. II.17 приведены результаты замеров азимутов падения швов тектонических брекчий в пределах минерализованной зоны трещиноватости. Если оценивать математическое ожидание азимутов падения прожилков по формуле , то получим =162°, что соответствует падению на юго-юго-восток. В то же время, по диаграмме розы наблюдений (см. рис. II.17) отчетливо видно, что основная масса прожилков имеет падение в северных румбах.

Таблица II.2. Замеры азимутов (в градусах) падения швов тектонических брекчий в пределах минерализованной зоны дробления

Азимут	Частота nj	Частость (nj/n)x100%	Азимут	Частота nj	Частость (nj/n)x100%
0–10	85	12,5	180–190	4	0,6
10–20	72	10,7	190–200	–	–
20–30	67	9,9	200–210	–	–
30–40	42	6,2	210–220	7	1,0
40–50	24	3,5	220–230	–	–
50–60	13	1,9	230–240	8	1,2
60–70	27	4,0	240–250	–	–
70–80	7	1,0	250–260	8	1,2
80–90	13	1,9	260–270	8	1,2
90–100	–	–	270–280	20	2,9
100–110	3	0,4	280–290	–	–
110–120	1	0,1	290–300	21	3,1
120–130	1	0,1	300–310	22	3,4
130–140	–	–	310–320	20	2,9
140–150	2	0,3	320–330	16	2,3
150–160	13	2,9	330–340	43	6,3
160–170	5	0,7	340–350	46	6,7
170–180	1	0,1	350–360	78	11,5

Рис. II.17. Диаграмма розы наблюдений азимутов падения швов тектонических брекчий в пределах минерализованной зоны дробления

В качестве характеристик положения угловых величин удобно использовать выборочное круговое среднее направление, выборочную круговую медиану и моду.

Если представить замеры угла (i=1, 2, ..., n) в виде точек на окружности – B_i, (см. рис. II.17), то выборочное круговое среднее направление определяется как направление суммы единичных векторов OB₁, …, OB_n. Если всем этим точкам приписать одинаковую «массу», равную , то координаты «центра масс» будут определяться формулами

и (II.1)

Длина суммарного вектора будет равна где , а направление этого вектора, то есть выборочное круговое среднее направление т, определяется из системы уравнений:

; (II.2)

Для сгруппированных данных формулы (II.1) принимают следующий вид: ; , где θ – средняя точка j-го интервала группировки (предполагается, что все интервалы имеют одинаковые длины , k–целое число), а n_j – частота, соответствующая j-му интервалу.

Расчеты выборочного кругового среднего направления для примеров, изображенных на рис. II.17 приведены в табл. II.3. Под таблицей приведен расчет кругового среднего по формулам (II.1) и (II.2).

Таблица II.3. Расчет выборочного кругового среднего направления азимутов падения швов тектонических брекчий (исходные данные в табл. II.2)

1	2	3	4	5	6
5	85	0,996	84,68	0,087	7,41
15	72	0,966	69,55	0,259	18,63
25	67	0,906	60,72	0,423	28,32
35	42	0,819	34,40	0,574	24,11
45	24	0,707	16,97	0,707	16,97
55	13	0,574	7,46	0,819	10,65
65	27	0,423	11,41	0,906	24,47
75	7	0,259	1,81	0,966	6,76
85	13	0,087	1,13	0,996	12,95
105	3	-0,259	-0,78	0,966	2,90
115	1	-0,423	-0,42	0,906	0,91
125	1	-0,574	-0,57	0,819	0,82
145	2	-0,819	-1,64	0,574	1,15
155	13	-0,906	-11,78	0,423	5,49
165	5	-0,966	-4,83	0,259	1,29
175	1	-0,996	-1,00	0,087	0,09
185	4	-0,966	-3,98	-0,087	-0,35
215	7	-0,819	-5,73	-0,574	-4,02
235	8	-0,574	-4,59	-0,819	-6,55
255	8	-0,259	-2,07	-0,966	-7,73
265	8	-0,087	-0,70	-0,966	-7.97
275	20	0,087	1,74	-0,996	-19,92
295	21	0,423	8,87	-0.906	-19,03
305	22	0,574	12,62	-0,819	-18,02

Продолжение таблицы II.3

1	2	3	4	5	6
315	20	0,707	14,14	-0,707	-14,14
325	16	0,819	13,11	-0,574	-9,18
335	43	0,906	38,97	-0,423	-18,17
345	46	0,966	44,43	-0,259	-11,91
355	78	0,996	77,70	-0,087	-6,80
Σ	677		461,63		19,11

; ;

; ;

; m = 2,37°.

Выборочной круговой медианой называется точка В на окружности, обладающая двумя свойствами:

– половина точек выборки лежит по одну сторону от диаметра BQ;

– большинство точек выборки ближе к В, чем к Q (см. рис. II.18).

Рис. II.18. Изображение замеров азимутов углов падения прожилков в виде точек на окружности

При малом количестве замеров эту характеристику можно легко найти по графику распределения точек на окружности. Так, например, очевидно, что для случая, приведенного на рис. II.18, свойствам выборочной круговой медианы удовлетворяет точка В₂,соответствующая азимуту падения 10°.

Для угловых измерений, наряду с модой, используют также характеристику, называемую антимодой. Она соответствует значению с минимальной частотой.

Для некоторых угловых величин (например, для азимутов падения пород в областях развития линейной складчатости) свойственны распределения с двумя модами, отстоящими друг от друга на 180°.

В качестве выборочной характеристики рассеяния угловых величин удобно использовать выборочную круговую дисперсию направлений, которая рассчитывается по формуле , где .

Указание

Решение произвести в электронных таблицах Excel.

В ячейку A1 введите название столбца «Азимут», в диапазон A2:A37 через меню Правка/Заполнить/Прогрессия… – числовой ряд от 5 до 355 – серединами интервалов, соответственно для каждого значения азимута в столбце B поместите значения частот из табл. II.3, в столбце C – рассчитайте значения частостей (относительных частот) в процентах. В столбце D следует рассчитать значения , в столбце E – , в столбце F – , в столбце G – . В ячейках B38, C38, E38, G38 – следует рассчитать суммы по соответствующим столбцам (см. рис. II.19). В ячейках B40:B42 по формулам (II.1) и (II.2) следует рассчитать координаты , , , в ячейках B43:B44 – значения cos(m) и sin(m) для расчета кругового среднего m, в ячейках B45:C46 – круговое среднее m, которое равно примерно 2,37°. Обратите внимание, что аргументы тригонометрических функций в электронных таблицах Excel задаются в радианах, поэтому для преобразования радианов в градусы при расчете кругового среднего использовать функцию ГРАДУСЫ. В ячейке B47 следует рассчитать выборочную круговую дисперсию направлений.

Рис. II.19. Расчет характеристик угловых величин

По данным столбцов A и B постройте гистограмму и лепестковую диаграмму (рис. II.20).

Рис. II.20. Построение гистограммы и диаграммы розы наблюдений

ИНТЕРВАЛЬНЫЕ ОЦЕНКИ СВОЙСТВ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ

Большинство геологических объектов отличается сильной изменчивостью свойств, определяемых по единичным замерам. Поэтому в практике геологических исследований часто возникает необходимость в оценке средних значений этих свойств и количественном выражении степени их изменчивости. Эти числовые характеристики используются при решении весьма широкого круга задач в различных областях геологии.

Статистические оценки могут быть точечными и интервальными. При точечной оценке неизвестная характеристика случайной величины оценивается некоторым числом, а при интервальной – некоторым интервалом значений. В пределах последнего с заданной вероятностью должно находиться истинное значение оцениваемой величины.

Точечная оценка не содержит информации о точности полученного результата. Чем меньше выборка и чем сильнее изменчивость признака, тем большей может оказаться ошибка. Поэтому в условиях малых выборок всегда желательно знать интервал значений признака, в который с заданной вероятностью попадает его неизвестное истинное среднее значение.

Пусть найденная по данным выборки статистическая характеристика Θ* служит оценкой неизвестного параметра Θ. Будем считать Θ постоянным числом (Θ может быть и случайной). Ясно, что Θ* тем точнее определяет параметр Θ, чем меньше абсолютная величина разности |Θ – Θ*|. Другими словами, если δ>0 и |Θ – Θ*|< δ, то тем меньше δ, тем оценка точнее. Таким образом, положительное число δ характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка Θ* удовлетворяет неравенству |Θ – Θ*|< δ; можно лишь говорить о вероятности γ, с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки Θ по Θ* называют вероятность γ, с которой осуществляется неравенство |Θ – Θ*|< δ. Обычно надежность оценки задается наперед, причем в качестве γ берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что |Θ – Θ*| < δ, равна γ:

P[ |Θ – Θ*| < δ ] = γ.

Заменив неравенство |Θ – Θ*|< δ равносильным ему двойным неравенством – δ < Θ – Θ* < δ, или Θ* – δ < Θ < Θ* + δ, имеем

P[ Θ* – δ < Θ < Θ* + δ ] = γ.

Это соотношение следует понимать так: вероятность того, что интервал (Θ* – δ, Θ* + δ) заключает в себе (покрывает) неизвестный параметр Θ, равна γ.

Доверительным называют интервал (Θ* – δ, Θ* + δ), который покрывает неизвестный параметр с заданной надежностью γ.

Замечание. Интервал (Θ* – δ, Θ* + δ) имеет случайные концы (их называют доверительными границами). Действительно, в разных выборках получаются различные значения Θ*. Следовательно, от выборки к выборке будут изменяться и концы доверительного интервала, т.е. доверительные границы сами являются случайными величинами – функциями от x₁, x₂, … , x_n.

Так как случайной величиной является не оцениваемый параметр Θ, а доверительный интервал, то более правильно говорить не о вероятности попадания Θ в доверительный интервал, а о вероятности того, что доверительный интервал покроет Θ.

Способ построения доверительного интервала для математического ожидания зависит от того, известно ли значение дисперсии σ². Если значение дисперсии известно, то доверительный интервал, соответствующий заданной надежности (доверительной вероятности) p, имеет вид

,

где – выборочная средняя, число t определяется из равенства 2Φ(t)=p, или Φ(t)= p/2; по таблице функции Лапласа находят аргумент t, которому соответствует значение функции Лапласа, равное p/2, n – объем выборки.

Достаточно малую вероятность, при которой (в данной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости. Обычно уровень значимости обозначают буквой α. Между доверительной вероятностью и уровнем значимости существует следующее соотношение

γ = 1 – α.

В Excel для построения доверительного интервала можно воспользоваться функцией ДОВЕРИТ, которая по заданным значениям уровня значимости α, σ и n вычисляет величину .

Функция ДОВЕРИТ(альфа; станд_откл; размер) определяет полуширину доверительного интервала и содержит следующие параметры:

• Альфа – уровень значимости, используемый для вычисления доверительной вероятности. Доверительная вероятность равняется 100*(1 - алъфа)% процентам, или, другими словами, альфа, равное 0,05, означает 95%-ный уровень доверительной вероятности;

• Станд_откл – стандартное отклонение генеральной совокупности для интервала данных, предполагается известным;

• Размер – это размер выборки.

В геологической практике дисперсия σ² изучаемой случайной величины обычно неизвестна, и вместо нее используется ее выборочная оценка s². Поэтому задача нахождения доверительных интервалов имеет лишь приближенные решения.

Когда значение дисперсии σ² неизвестно, для определения границ доверительного интервала для среднего можно воспользоваться формулой

,

где – выборочная средняя, s – стандартное отклонение, t_n,p – табличное значение распределения Стьюдента с числом степеней свободы k = n–1 и доверительной вероятностью p, n – количество элементов в выборке.

В Excel для более точного вычисления границ доверительного интервала и при числе элементов в выборке п < 30 можно воспользоваться функцией Уровень надежности: X% процедуры Описательная статистика, которая вычисляет границы доверительного интервала для неизвестного математического ожидания с доверительным уровнем X%; доверительный интервал строится как выборочное среднее плюс-минус данное значение. Граница вычисляется с помощью распределения Стьюдента, то есть здесь неявно используется предположение о нормальности распределения генеральной совокупности.

Одним из важных вопросов, возникающих при анализе выборки, является вопрос: относится та или иная варианта к данной статистической совокупности? Если распределение совокупности является нормальным, можно использовать правило трех сигм. Согласно этому правилу, как уже говорилось выше, в пределах находится 99,7% всех вариант. Поэтому, если варианта попадает в этот интервал, то она считается принадлежащей к данной совокупности. Если не попадает, то она может быть отброшена.

Примечание. Практически при n > 30 можно вместо распределения Стьюдента пользоваться нормальным распределением. Важно подчеркнуть, что для малых выборок (n < 30), в особенности для малых значений n, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, то есть к повышению точности оценки. Например, если n = 5 и γ = 0,99, то, пользуясь распределением Стьюдента, найдем t_γ = 4,6, а используя функцию Лапласа, найдем t_γ = 2,58, то есть доверительный интервал в последнем случае окажется более узким. Чем найденный по распределению Стьюдента. То обстоятельство, что распределение Стьюдента при малой выборке дает не вполне определенные результаты (широкий доверительный интервал), вовсе не свидетельствует о слабости метода Стьюдента, а объясняется тем, что малая выборка, разумеется, содержит малую информацию об интересующем нас признаке.

ПРИМЕР II.6

Вернемся к задаче определения петрографического типа породы из горизонта неогеновых лав (см. табл. I.1). Более корректно допрос о названии данной породы можно решить путем расчета интервальной оценки среднего содержания. Расчеты оценок асимметрии и эксцесса показывают, что гипотеза о соответствии эмпирических данных нормальному закону распределения не отвергается. Это позволяет для расчета интервальной оценки среднего содержания SiO₂ в лавах воспользоваться функцией ДОВЕРИТ.

Требуется

Найти границы 95%-ного доверительного интервала для среднего значения по данным табл. I.1.

Решение

1. Откройте новую рабочую таблицу. Установите табличный курсор в ячейку А1. Столбец A заполнить значениями содержаний SiO₂ (в %) в неогеновых лавах (ячейки A1:A30). В ячейку A31 введите функцию =СЧЕТ(A1:A30), в ячейку A32 введите функцию =СТАНДОТКЛОН(A1:A30), в ячейку A33 введите формулу =1–0,95, в ячейку A34 введите функцию =СРЗНАЧ(A1:A30).

2. Установите табличный курсор в ячейку C32. Для определения границ доверительного интервала необходимо на панели инструментов Стандартная нажать кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ДОВЕРИТ, после чего нажмите кнопку OK.

3. В рабочие поля появившегося диалогового окна ДОВЕРИТ введите условия задачи: Альфа – A33; Станд_откл – A32; Размер – A31. Нажмите кнопку OK. Имеем значение полуширины интервала (1,567726).

4. В ячейке C32 появится полуширина 95%-ного доверительного интервала для среднего значения выборки – 1,567726. В ячейку С34 введите формулу =A34–C32, в ячейку D34 введите формулу =A34+C32. Таким образом, с вероятностью 0,95 истинное среднее содержание SiO₂ в породах данного горизонта находится в интервале от 63,99% до 67,13%, то есть не выходит за пределы, установленные для дацита: 63,0 – 68,5%.

ПРИМЕР II.7

Требуется

По результатам предыдущего примера необходимо определить границы 95%-ного доверительного интервала для среднего значения с использованием пакета анализа.

Решение

1. Продолжим вычисления на листе предыдущего примера.

2. Далее вызовите процедуру Описательная статистика. Для этого, указав курсором мыши на пункт меню Сервис, выберите команду Анализ данных. Затем в появившемся списке Инструменты анализа выберите строку Описательная статистика.

3. В появившемся диалоговом окне в рабочем поле Входной интервал: укажите входной диапазон – А1:А30. Переключателем активизируйте Выходной интервал и укажите выходной диапазон – ячейку F32. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в левое поле Уровень надежности: и в правом поле (%) – 95. Затем нажмите кнопку OK.

4. В результате анализа в указанном выходном диапазоне для доверительной вероятности 0,95 получаем значения доверительного интервала.

Уровень надежности – это половина доверительного интервала для генерального среднего арифметического. Из полученного результата следует, что с вероятностью 0,95 среднее арифметическое для генеральной совокупности находится в интервале 65,56 ± 1,63. Здесь 65,56 – выборочное среднее для рассматриваемого примера, которое находится обычно процедурой Описательная статистика одновременно с доверительным интервалом.

Для вычисления доверительного интервала можно воспользоваться формулой . Допустимое значение распределения Стьюдента t_n,p с числом степеней свободы k = n–1 и доверительной вероятностью p может быть определено по приложению II. Для объема выборки п = 30 и уровня значимости α=0,05 значение распределения Стьюдента t_n,p = 2,04. Введем это число в свободную ячейку A41. Тогда в ячейке A42 можно рассчитать по формуле =B41*A32/(A31)^(1/2) значение . Допустимое значение распределения Стьюдента t_n,p для п = 30 и α =0,05 может быть определено с помощью формулы Excel =СТЬЮДРАСПОБР(0,05;30), которую введем в ячейку B41. Тогда в ячейку B42 введем формулу =B41*A32/(A31)^(1/2) для расчета .

5. Для нахождения доверительных границ для «выскакивающей» варианты необходимо полученный выше доверительный интервал умножить на (в примере – , то есть 1,63* = 9,975). В Excel это можно выполнить следующим образом. Табличный курсор установите в свободную ячейку H47; введите с клавиатуры знак =; мышью укажите на ячейку в которой находится результат вычислений половины доверительного интервала для генерального среднего арифметического – G47; введите с клавиатуры знак *; с панели инструментов Стандартная вызовите Вставка функции (f_x); выберите категорию Математические, тип функции Корень; нажмите OK, введите с клавиатуры число п = 30 и нажмите OK. В результате получим в ячейке С4 значение доверительного интервала – 8,96.

Таким образом, варианта, попадающая в интервал 65,56 ± 8,96, считается принадлежащей данной совокупности с вероятностью 0,95. Выходящая за эти границы варианта может быть отброшена с уровнем значимости α = 0,05.

Проверьте и убедитесь, что все варианты входят в указанный интервал доверительных границ.

Способы построения доверительных интервалов не только позволяют найти величины возможных ошибок при оценке средних значений изучаемых свойств по выборочным данным, но могут также использоваться для решения обратной задачи, то есть для нахождения объема выборки, обеспечивающей получение оценок с заданной точностью. Задача определения оптимального числа выборочных данных при исследовании геологических объектов возникает постоянно и является весьма важной, особенно при разведке месторождений, когда каждое выборочное наблюдение требует проходки специальной горной выработки или бурения скважины.

Для решения обратной задачи в случае нормального распределения исследуемой случайной величины можно воспользоваться формулой .

При малом объеме выборки (n < 60) величина t зависит от n, поэтому для решения обратной задачи используется способ последовательного приближения. Первоначально в формулу подставляется значение распределения Стьюдента t для n = ∞.

Если полученное п₁ окажется меньше 60, в формулу подставляется значение t для полученного п₁, и эта операция повторяется до тех пор, пока полученное в результате очередного расчета значение п_i, не совпадет с величиной п_i-1, принятой для определения t при ее расчете.

ПРИМЕР II.8

Требуется

В ПРИМЕРАХ II.6 – II.7 расчет интервальной оценки среднего содержания SiO₂ в эффузивных породах по 30 пробам показал, что с вероятностью 0,95 возможная ошибка составляет приблизительно ±1,6% SiO₂. Определим число проб, необходимое для того, чтобы с той же вероятностью ошибка в определении среднего содержания не превысила 1% SiO₂.

1. Продолжим вычисления на листе предыдущих ПРИМЕРОВ II.6 – II.7.

2. В свободной ячейке A45 запишем формулу =СТЬЮДРАСПОБР(0,05;10^10) для определения значение распределения Стьюдента t для n = ∞. В ячейке A46 запишем =(A45*A32)^2. Получим около 74. То есть n₁ = 74. В ячейке A47 запишем формулу =СТЬЮДРАСПОБР(0,05;74) для определения значение распределения Стьюдента t для n₁ = 74. В ячейке A48 запишем =(A47*A32)^2. Получим около 77. То есть n₂ = 77. В ячейке A49 запишем формулу =СТЬЮДРАСПОБР(0,05;77) для определения значение распределения Стьюдента t для n₂ = 77. Значения и практически совпадают, поэтому в дальнейших расчетах нет необходимости.

ЛАБОРАТОРНАЯ РАБОТА № III. ОДНОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГЕОЛОГИЧЕСКИХ ГИПОТЕЗ

Решение многих геологических задач основано на принципе аналогии, когда для объяснения особенностей строения слабо изученных объектов используют закономерности, установленные при изучении аналогичных объектов. Для правильного выбора объекта-аналога необходимо оценить степень его сходства с исследуемым объектом.

В других случаях (например, при интерпретации многих геофизических данных) возникает необходимость оценить степень различия геологических объектов по тем или иным физическим свойствам.

Для объективного решения вопроса о сходстве или различии, геологических объектов используются статистические методы проверки гипотез о равенстве числовых характеристик их свойств. В геологической практике чаще всего эти методы применяются для суждения:

• о равенстве средних значений изучаемого признака, полученных разными методами для одного и того же объекта или одним методом для различных объектов;

• о равенстве дисперсий двух случайных величин по выборочным данным;

об однородности изучаемого объекта.

Статистическая проверка гипотез производится с помощью критериев согласия.

Критерием согласия называется значение некоторой функции K=f(X₁, X₂, ..., X_n), где X₁, X₂, ..., X_n – случайные величины, характеризующие проверяемую гипотезу. Функция выбирается таким образом, чтобы в случае правильности проверяемой гипотезы ее значения представляли бы собой случайную величину с заранее известным распределением.

Проверяемая гипотеза принимается, если значение K, вычисленное через выборочные значения величин X₁, X₂, ..., X_n, окажется меньше или больше (в зависимости от формулировки гипотезы) теоретического значения K для аналогичных условий и заданной вероятности α, которое берется по известному распределению. Вероятность α при этом соответствует уровню вероятности практически невозможного события и называется уровнем значимости.

Соответственно вероятность (1 – α), определяющая область, в пределах которой правильность принятого решения будет практически достоверным событием, называется доверительной.

Ошибка, заключенная в непринятии гипотезы, в действительности являющейся справедливой, называется ошибкой первого рода, а принятие ложной гипотезы – ошибкой второго рода.

Если вероятность ошибки второго рода обозначить через β, то (1 – β), то есть вероятность отсутствия такой ошибки, будет величиной, называемой мощностью данного критерия относительно конкурирующей гипотезы.

Увеличение доверительной вероятности (уменьшение уровня значимости) снижает вероятность ошибки первого рода, но увеличивает вероятность ошибки второго рода.

Область применения определенных критериев согласия обычно ограничивается некоторыми условиями, а их мощность зависит от характера конкурирующей (альтернативной) гипотезы и объема выборки.

Для решения задач на основе статистической проверки гипотез геолог должен выполнить следующие операции:

• четко сформулировать проверяемую (Н₀) и альтернативную (Н₁) гипотезу исходя из существа поставленной геологической задачи;

• выбрать наиболее мощный при данном объеме выборки критерий, условия применения которого не противоречат свойствам изучаемых случайных величин;

• оценить последствия ошибки первого и второго рода в условиях решаемой геологической задачи и выбрать уровень значимости исходя из требования минимизации ущерба в результате неправильного решения;

• рассчитать эмпирическое значение критерия согласия K по выборочным данным, сравнить его с теоретическим значением K для принятого уровня значимости и принять решение относительно гипотезы Н₀,

• интерпретировать полученный результат применительно к поставленной геологической задаче.

При формулировке проверяемой гипотезы Н₀ трудностей обычно не возникает, однако вопрос о том, какую гипотезу принять в качестве альтернативной не всегда решается однозначно, так как для одной и той же гипотезы Н₀ может существовать несколько альтернативных гипотез Н₁. Например, при расчете интервальных оценок гипотеза Н₀ заключается в том, что неизвестное математическое ожидание Mx находится в определенном интервале значений, то есть

.

В то же время в качестве альтернативных могут выступать разные гипотезы:

• математическое ожидание меньше нижней границы доверительного интервала, то есть

;

• математическое ожидание больше верхней границы доверительного интервала, то есть

;

• математическое ожидание больше верхней или меньше нижней границы доверительного интервала, то есть

.

В качестве альтернативной гипотезы может быть принята гипотеза . Однако при подсчете запасов месторождений часто целесообразнее пользоваться альтернативной гипотезой , так как вопрос возможности промышленного использования определенных объемов руды решается путем сравнения полученных данных оценок среднего содержания полезного компонента с минимальным промышленным содержанием.

Неправильная формулировка альтернативной гипотезы может вызвать ошибки при пользовании статистическими таблицами, поскольку существуют таблицы для критериев двух типов – односторонних и двусторонних. В таблицах односторонних критериев приводятся доверительные вероятности или уровни значимости, соответствующие простым альтернативным событиям типа или . Таблицы двусторонних критериев построены для сложных альтернатив типа , когда учитывается вероятность сразу двух событий.

Интегральная функция Лапласа (см. приложение I) относится к таблицам первого типа, поэтому при нахождении по ней вероятностного критерия Z для построения двустороннего доверительного интервала, то есть при альтернативе , уровень значимости необходимо уменьшать и два раза. Таблицы второго типа строятся только для симметрично распределенных критериев. Они более компактны и удобны для построения доверительных интервалов и проверки гипотез при альтернативах типа . Примером таблиц этого типа является таблица двустороннего t-критерия Стьюдента (см. приложение II). Используя эту таблицу для построения односторонних доверительных интервалов или проверки гипотез при альтернативах типа или значения функции принимаются для уровня значимости 2α.

Статистические критерии согласия разделяются на параметрические и непараметрические. Параметрические критерии выводятся из свойств тех или иных статистических законов распределения и могут использоваться лишь в том случае, если распределение выборочных данных согласуется с этим законом. Непараметрические критерии могут применяться даже в том случае, если закон распределения изучаемых величин неизвестен или их распределения не соответствуют никакому из известных законов. Непараметрические критерии обычно обладают несколько меньшей мощностью по сравнению с параметрическими аналогами, но область их применения значительно шире. Фактические распределения свойств геологических объектов часто отклоняются от теоретических, поэтому геологи проявляют большой интерес к непараметрическим критериям.

Выбор уровня значимости при статистической проверке гипотез является весьма важным, но отнюдь не всегда простым вопросом. Он решается исключительно исходя из особенностей геологической задачи на основе анализа возможных последствий от ошибок первого и второго рода. Для правильного выбора уровня значимости геологу необходимо четко представлять себе конечную цель проводимых исследований, а иногда даже выполнять укрупненные технико-экономические расчеты для оценки возможного ущерба за счет принятия неправильного решения. В случае затруднения с выбором уровня значимости гипотезу целесообразно проверить при разных его значениях.

При интерпретации полученных результатов необходимо следить за тем, чтобы вывод по геологической задаче строго логически соответствовал проверяемой гипотезе Н₀.

ПРОВЕРКА ГИПОТЕЗ О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ

Большинство статистических методов решения геологических задач основано на использовании свойств тех или иных законов распределения. Однако геолог обычно не может заранее знать, какими свойствами будут обладать полученные в результате исследования выборочные совокупности. Поэтому решению конкретных задач предшествует этап сравнения эмпирических распределений с известными теоретическими.

Проверка соответствия теоретическому распределению. В большинстве случаев при решении реальных задач закон распределения и его параметры неизвестны. В то же время применяемые статистические методы в качестве предпосылок часто требуют определенного закона распределения. Отсюда, важной задачей, возникающей при анализе одной выборки, является оценка меры соответствия (расхождения) полученных эмпирических данных и каких-либо теоретических распределений. Наиболее часто проверяется предположение о нормальном распределении генеральной совокупности, поскольку большинство статистических процедур ориентировано на выборки, полученные из нормально распределенной генеральной совокупности.

Для оценки соответствия имеющихся экспериментальных данных нормальному закону распределения обычно используют графический метод, выборочные параметры формы распределения и критерии согласия.

Графический метод позволяет давать ориентировочную оценку расхождения или совпадений распределений.

При большом числе наблюдений (п > 100) неплохие результаты дает вычисление выборочных параметров формы распределения: эксцесса и асимметрии. Принято говорить, что предположение о нормальности распределения не противоречит имеющимся данным, если асимметрия близка к нулю, то есть лежит в диапазоне от -0,2 до 0,2, а эксцесс – от -1 до 1.

Наиболее убедительные результаты дает использование критериев согласия. Критериями согласия называют статистические критерии, предназначенные для проверки согласия опытных данных и теоретической модели. Здесь нулевая гипотеза Н₀ представляет собой утверждение о том, что распределение генеральной совокупности, из которой получена выборка, не отличается от нормального. Среди критериев согласия большое распространение получил непараметрический критерий χ² (хи-квадрат). Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитанными по формулам нормального распределения.

Отметим, что сколько-нибудь уверенно о нормальности закона распределения можно судить, если имеется не менее 50 результатов наблюдений. В случаях меньшего числа данных можно говорить только о том, что данные не противоречат нормальному закону, и в этом случае обычно используют графические методы оценки соответствия. При большем числе наблюдений целесообразно совместное использование графических и статистических (например, тест хи-квадрат или аналогичные) методов оценки, естественно дополняющих друг друга.

Использование критерия согласия хи-квадрат. Для применения критерия желательно, чтобы объем выборки п ≥ 40, выборочные данные были сгруппированы в интервальный ряд с числом интервалов не менее 7, а в каждом интервале находилось не менее 5 наблюдений (частот).

Отметим, что сравниваться должны именно абсолютные частоты, а не относительные (частости). При этом, как и любой другой статистический критерий, критерий хи-квадрат не доказывает справедливость нулевой гипотезы (соответствие эмпирического распределения нормальному), а лишь может позволить ее отвергнуть с определенной вероятностью (уровнем значимости).

Для критерия хи-квадрат как и в случае с критерием Стьюдента, принимается нулевая гипотеза о том, что выборки принадлежат к одной генеральной совокупности. Кроме того, определяется ожидаемое значение результата. Обычно это среднее значение между выборками рассматриваемого показателя. Затем оценивается вероятность того, что ожидаемые значения и наблюдаемые принадлежат к одной генеральной совокупности.

В Excel критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2ТЕСТ вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что наблюдаемые значения не соответствуют нормальному закону распределения. Если вычисленная вероятность близка к 1, то можно говорить о высокой степени соответствия экспериментальных данных нормальному закону распределения.

Функция имеет следующие параметры: ХИ2ТЕСТ(фактический_интервал; ожидаемый_интервал). Здесь:

• фактический_интервал – это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями;

• ожидаемый_интервал – это интервал данных, который содержит теоретические (ожидаемые) значения для соответствующих наблюдаемых.

Принятие гипотезы о соответствии изучаемого свойства определенному закону не исключает возможного соответствия этих же выборочных данных другому теоретическому распределению. В геологической практике нередки случаи, когда по выборочным данным не отвергается гипотеза о их соответствии как нормальному, так и логнормальному закону, а распределения дискретных случайных величин могут удовлетворительно аппроксимироваться как биномиальным, так и нормальным законами и т.п. В этих случаях при выборе теоретической модели распределения необходимо учитывать характер решаемой геологической задачи, свойства оценок параметров распределений различного типа по выборкам имеющегося объема и наличие соответствующих статистических таблиц. При этом предпочтение следует отдавать наиболее простым и хорошо изученным распределениям.

ПРИМЕР III.1

Требуется

Проверить соответствие выборочных данных эмпирического распределения содержания SiO₂ в неогеновых лавах для выборки (см. табл. I.1) нормальному закону распределения, используя пакет Excel.

Решение

Решение данного примера до п. 7 совпадает с решением ПРИМЕРА II.1.

1. В ячейку А1 введите заголовок Наблюдения, а в диапазон А2:A31 – значения (в %) содержания SiO₂ в неогеновых лавах. В ячейке A32 подсчитайте максимальное значение, в ячейке A33 – минимальное значение.

2. Выберите ширину интервала 1%. Тогда при крайних значениях 56% и 74% получится 18 интервалов. В ячейку D1 введите название Границы интервалов. В диапазон D2:D20 введите через меню Правка/Заполнить/Прогрессия… числовой ряд от 56 до 74 (56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74).

3. Введите заголовки создаваемой таблицы: в ячейки E1 – Абсолютные частоты, в ячейки F1 – Относительные частоты.

4. Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек E2:E20 (используемая функция ЧАСТОТА задается в виде формулы массива). С панели инструментов Стандартная вызовите Мастер функций (кнопка f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ЧАСТОТА, после чего нажмите кнопку OK. Появившееся диалоговое окно ЧАСТОТА необходимо за серое поле мышью отодвинуть вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши в рабочее поле Массив_данных введите диапазон данных наблюдений (А2:A31). В рабочее поле Двоичный_массив мышью введите диапазон интервалов (D2:D20). Последовательно нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце E2:E20 появится массив абсолютных частот.

5. В ячейке E21 найдите общее количество наблюдений. Табличный курсор установите в ячейку E21. На панели инструментов Стандартная нажмите кнопку Автосумма. Убедитесь, что диапазон суммирования указан правильно (E2: E20), и нажмите клавишу Enter. В ячейке E21 появится число 30.

6. Заполните столбец относительных частот. В ячейку F2 введите формулу для вычисления относительной частоты: =E2/E$21. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон F3:F20. Получите массив относительных частот.

7. Найдите теоретические частоты нормального распределения. Для этого предварительно необходимо найти среднее значение и стандартное отклонение выборки.

В ячейке A34 с помощью функции СРЗНАЧ найдите среднее значение для данных из диапазона А2:A31 (65,57). В ячейке A35 с помощью функции СТАНДОТКЛОН найдите стандартное отклонение для этих же данных (4,38). В ячейки G1 введите название столбца – Теоретические частости. Затем с помощью функции НОРМРАСП найдите теоретические частости. Установите курсор в ячейку G2, вызовите указанную функцию и заполните ее рабочие поля: х– D2; Среднее - $A$34; Стандартное_откл – $A$35. Интегральный – 0. Получим в ячейке G2 – 0,0083. Далее протягиванием скопируйте содержимое ячейки G2 в диапазон ячеек G3:G20. Затем в ячейки H1 введите название нового столбца – Теоретические частоты. Установите курсор в ячейку H2 и введите формулу =E$21*G2. Далее протягиванием скопируйте содержимое ячейки H2 в диапазон ячеек H3:H20. В ячейке H21 с помощью функции СУММ найдите среднее значение для данных из диапазона Н2:H20 (29,07). В результате у вас получится как на рис. III.1.

8. С помощью функции ХИ2ТЕСТ определите соответствие данных нормальному закону распределения. Для этого установите табличный курсор в свободную ячейку I21. На панели инструментов Стандартная нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ХИ2ТЕСТ, после чего нажмите кнопку OK. Появившееся диалоговое окно ХИ2ТЕСТ отодвиньте вправо на 1–2 см от данных. Указателем мыши в рабочие поля введите фактический E2:E20 и ожидаемый H2:H20 диапазоны частот. Нажмите кнопку OK. В ячейке I21 появится значение вероятности того, что выборочные данные соответствуют нормальному закону распределения – 0,56.

9. Поскольку полученная вероятность соответствия экспериментальных данных р = 0,56 много больше, чем уровень значимости α =1 – р = 0,05, то можно утверждать, что нулевая гипотеза не может быть отвергнута и, следовательно, данные не противоречат нормальному закону распределения.

Рис. III.1. Результат вычислений относительных и теоретических частот

ЗАДАЧА III.1

Требуется

По результатам предыдущего примера построить гистограммы абсолютных и теоретических частот (см. рис. III.2).

Рис. III.2. Гистограммы абсолютных и теоретических частот

ПРИМЕР III.2

Требуется

Проверить соответствие выборочных данных эмпирического распределения содержания SiO₂ в неогеновых лавах для выборки (см. табл. I.1) нормальному закону распределения, используя пакет STATISTICA.

Решение

В системе STATISTICA создается файл данных, используя числовую таблицу I.1. Через меню Data/Cases/Add… вызвать диалоговое окно Add Cases (см. рис. III.3) добавить 20 строк к существующим по умолчанию десяти. Через меню Data/Vars/Delete… удалить столбцы, начиная со второго по десятый (см. рис. III.4). Далее привести документ к виду, показанному на рис. III.5, заполнив столбцы данными табл. I.1. Сохранить файл.

Рис. III.3. Заполнение диалогового окна Add Cases

Рис. III.4. Заполнение диалогового окна Delete Variables

Рис. III.5. Заполнение столбца Var1 исходными данными

В меню Statistics программы STATISTICA выбирается пункт Basic Statistics/Tables и далее раздел Descriptive statistics – расчет описательных статистик (рис. III.6). В диалоговом окне Descriptive Statistics нажимается кнопка Variables (переменная) (рис. III.7). Укажите переменную Var1.

Рис. III.6. Выбор подпункта Descriptive statistics

Рис. III.7. Ввод имени переменной для исследования

В диалоговом окне Descriptive Statistics выбирается вкладка Advanced, где отметим показатели, которые требуется вычислить: Valid N (объем выборки), Mean (среднее), Standart Deviation (среднее квадратическое отклонение), Conf. limits for means interval (доверительный предел для среднего) – по умолчанию установлен 95,00%, Minimum & maximum (минимум и максимум). Нажмите одну из кнопок Summary (итог). Результаты расчета показаны на рис. III.8. Доверительный интервал на 5 % уровне значимости имеет границы: (63,93074;67,20260).

Рис. III.8. Результаты расчета числовых характеристик выборки

Рассмотрим проверку гипотезы о виде распределения по критерию χ² (хи-квадрат). Запустите в меню Statistics программы STATISTICA Distribution Fitting. Далее в Continuous Distributions (непрерывное распределение) выберите Normal (нормальное распределение) – рис. III.9. Нажмите OK.

Рис. III.9. Выбор вида распределения

В диалоговом окне Fitting Continuous Distributions нажмите на кнопку Variables (переменная). Укажите переменную Var1.

Число интервалов группировки определяется автоматически. Пользователь может изменить число интервалов группировки или принять значение, предлагаемое программой. На вкладке Parameters введем для Number of categories (число категорий) число 11 вместо установленного по умолчанию значения (Set to default) 21 – см. рис. III.10. Нижний предел (Lower limit) установлен по умолчанию – 54. Верхний предел (Upper limit) – 75. Среднее (Mean) – 65,56666667. Дисперсия (Variance) – 19,19402299.

Рис. III.10. Задание числа категорий

На вкладке Options установим флажок для Chi-Square test (хи-квадрат тест), который позволяет изменять ожидаемые частоты интервалов для расчета хи-квадрат тест: If expected bin-frequency is less than or equal 5, then combine with adjacent bins (Если ожидаемая частота интервала меньше или равная чем 5, их следует объединять со смежными интервалами) – рис. III.11. Нажмите Summary (итог). Результаты расчета показаны на рис. III.12.

Рис. III.11. Установка ожидаемых частот для расчета теста хи-квадрат

Рис. III.12. Результаты расчета числовых характеристик интервалов

В полученной таблице (рис. III.12) в столбце Observed Frequency – наблюдаемые частоты, Cumulative Observed – наблюдаемые накопленные частоты, Percent Observed – наблюдаемые проценты, Cumul. % Observed – наблюдаемые накопленные проценты, Expected Frequency – ожидаемые частоты, Cumulative Expected – ожидаемые накопленные частоты, Percent Expected – ожидаемые проценты, Cumul. % Expected – ожидаемые накопленные проценты, Observed-Expected – разность между наблюдаемыми и ожидаемыми частотами.

В верхней части таблицы указана величина рассчитанного значения теста хи-квадрат (Chi-Square test) – 1,29523, число степеней свободы для объединенных интервалов (d.f. = 1(adjusted)), вычисленный уровень значимости – p=0,25509. Поскольку вычисленный уровень значимости значительно превышает установленный уровень значимости α =1 – р = 0,05, то можно утверждать, что нулевая гипотеза не может быть отвергнута и, следовательно, данные не противоречат нормальному закону распределения.

Для построения графиков частот в левом нижнем углу нажмите кнопку свернутого диалогового окна Fitting Continuous Distributions и вернитесь в диалоговое окно. Откройте вкладку Quick и нажмите на кнопку Plot of observed and expected distribution (график наблюдаемого и ожидаемого распределений). Получите график, представленный на рис. III.13.

Рис. III.13. Результаты построения графиков частот

ПРИМЕР III.3

На месторождении алмазоносных кимберлитов отобрано 200 проб массой 2 т. В каждой пробе обнаружено от 0 до 4 алмазов размером больше 1 мм. Число проб п_i, с разным количеством i алмазов класса +1 мм приведено в табл. III.1.

Таблица III.1. Проверка гипотезы о соответствии распределения количества алмазов в пробах по закону Пуассона

i	ni	λi	Pi		ni –
0	123	0	0,589	117,7	5,279	27,87	0,237
1	53	53	0,312	62,39	-9,39	88,21	1,414
2	20	40	0,083	16,53	3,466	12,01	0,727
3	3	9	0,015	2,921	0,079	0,006	0,002
4	1	4	0,002	0,387	0,613	0,376	0,971

Требуется

Проверить гипотезу о соответствии распределения количества алмазов по закону Пуассона.

Решение

Если число испытаний велико, а вероятность появления случайного события в каждом испытании очень мала, то для описания вероятностей того, что событие А в серии из п испытаний произойдет Х раз, используется распределение Пуассона: (где λ=пр, то есть среднее число появления события А в п испытаниях).

Гипотезу о соответствии распределения закону Пуассона также можно проверить с помощью критерия χ².

В серии из N испытаний случайное событие может реализоваться в каждом испытании i раз. При этом i = 0, 1, 2, ..., r, где r – максимальное число наблюдавшихся событий в одном испытании, а n_i – количество испытаний, когда случайное событие наблюдалось i раз. По выборочным данным находят оценку средней вероятности случайного события:

(III.1)

Подставив ее в формулу распределения Пуассона

(III.2)

рассчитывают теоретические вероятности P_i, появления ровно i событий в одном испытании в серии из N испытаний. Теоретические частоты таких случаев в серии из испытаний находят по формуле . Затем по разнице теоретических ( ) и фактических (n_i) частот определяют эмпирическое значение критерия χ², которое сравнивают с табличным для заданного уровня значимости α и числа степеней свободы K=s–2, где s – число различных групп выборки, обычно совпадающее с количеством наблюдавшихся различных вариантов реализации случайного события в одном испытании, то есть s=r+1. Исключение составляют случаи, когда теоретические частоты для некоторых значений i очень малы (меньше 5). Обычно это группы наблюдений, где i близко к r. Тогда теоретические и фактические частоты для соседних групп наблюдений суммируются, и общее количество групп уменьшается.

1. Вычисления следует располагать так, как показано на рис. III.14.

Рис. III.14. Проверка гипотезы о соответствии распределения количества алмазов в пробах по закону Пуассона

В ячейки A2:A6 поместите значения i событий из табл. III.1, в ячейки B2:B6 – значения n_i из табл. III.1. В ячейке B7 рассчитайте сумму столбца B – 200 проб. В ячейках C2:C6 следует рассчитать оценку средней вероятности случайного события λ_i по формуле (III.1), которая будет выглядеть для ячейки С2 как =A2*B2. В ячейке С7 рассчитайте сумму по формуле , для чего введите в ячейку =B2*A2+B3*A3+B4*A4+B5*A5+B6*A6.

Средняя вероятность ( ) попадания кристалла в пробу равна:

и может быть рассчитана в ячейке C8 делением ячейки С7 на B7.

Следовательно, формула закона Пуассона принимает вид

.

Рассчитанные по этой формуле значения теоретических вероятностей приведены на рис. III.14 в ячейках D2:D6 – теоретические вероятности P_i по формуле (III.2), которая будет выглядеть для ячейки D2 как =(($C$8^A2)*(EXP(1)^(-$C$8))/ФАКТР(A2)).

Теоретические частоты получают путем умножения значений P_i, на объем выборки равный 200 (столбец E, рис. III.14): в ячейку E2 вводится формула =D2*$B$7.

В столбце F рассчитывается разность между эмпирическими и теоретическими частотами: в ячейку F2 вводится формула =B2–E2, в столбце G эта разность возводится в квадрат: в ячейку G2 вводится формула =F2^2, а в столбце H этот квадрат делится на значение соответствующей теоретической частоты: в ячейку H2 вводится формула =G2/E2. В ячейке H7 вводится с помощью кнопки Автосумма панели инструментов формула =СУММ(H2:H6). Это и есть эмпирическое значение критерия для данной выборки.

Эмпирическое значение критерия для данной выборки примерно равно 3,35. По таблицам распределения (см. приложение III) при α=0,05 и числе степеней свободы K=4 – 2 = 2 находится критическое значение: .

Критическое значение критерия при α=0,05 и числе степеней свободы K = 2 может быть найдено в пакете Excel с помощью функции ХИ2ОБР. В ячейку A10 введите формулу =ХИ2ОБР(0,05;2). Критическое значение критерия по этой формуле равно примерно 5,991.

Так как , то нет оснований отвергать гипотезу о соответствии распределения алмазов класса +1 мм в пробах массой 2 т закону Пуассона.

2. Этот пример может быть решен проще с помощью функции ПУАССОН, позволяющей рассчитать теоретические вероятности P_i, и функции ХИ2ТЕСТ, позволяющей установить соответствие данных заданному закону распределения.

В ячейку J1 введите название столбца – Теоретические вероятности. В ячейку J2 введите формулу =ПУАССОН(A2;$C$8;0), которую затем скопируйте в диапазон J2:J6. В ячейку K1 введите название столбца – Теоретические частоты. В ячейку K2 введите формулу =J2*$B$7, которую затем скопируйте в диапазон K2:K6.

С помощью функции ХИ2ТЕСТ определите соответствие данных заданному закону распределения. Для этого установите табличный курсор в свободную ячейку H9. На панели инструментов Стандартная нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ХИ2ТЕСТ, после чего нажмите кнопку OK. Появившееся диалоговое окно ХИ2ТЕСТ отодвиньте вправо на 1-2 см от данных. Указателем мыши в рабочие поля введите фактический B2:B6 и ожидаемый K2:K6 диапазоны частот. Нажмите кнопку OK. В ячейке H9 появится значение вероятности того, что выборочные данные соответствуют нормальному закону распределения – 0,501.

Поскольку полученная вероятность соответствия экспериментальных данных р = 0,501 много больше, чем уровень значимости α =1 – р = 0,05, то можно утверждать, что нулевая гипотеза не может быть отвергнута и, следовательно, данные не противоречат закону распределения Пуассона.

ЗАДАЧА III.2

Случайная угловая величина называется равномерно распределенной, если ее плотность распределения вероятностей выражается формулой .

Для этого случая характерно отсутствие концентрации значений около какого-нибудь направления. Выборочные значения имеют максимальный разброс, поскольку угловая дисперсия при этом распределении равна 1.

Это распределение характерно, например, для замеров ориентировки обломков в делювиальных отложениях и эруптивных брекчиях.

Проверка гипотезы о равномерном распределении угловой величины при малом объеме выборки осуществляется с помощью критерия равномерности Релея. По выборочным данным вычисляется статистика , где , a , которая сравнивается с ее критическим значением для этого объема выборки п и принятого уровня значимости α (см. приложение IV.).

При п > 100 можно воспользоваться тем, что величина распределена приближенно по закону с двумя степенями свободы.

Критические значения этой величины для различных уровней значимости также приведены в приложении IV.

На месторождении бокситов, отработка которого ведется открытым способом, за 5 лет произошло 19 случаев оползания бортов карьера. Распределение этих случаев по различным месяцам приведено в графе 2 табл. III.2. На основании этих данных высказано предположение, что устойчивость бортов карьера снижается в весенний период.

Требуется

Оценить обоснованность того, что устойчивость бортов карьера снижается в весенний период путем проверки гипотезы о равномерном распределении случаев оползания бортов карьера в течение года.

Указание

Рассматривая год как цикл с периодом 2π, определить, что каждому месяцу будет соответствовать интервал на окружности, равный 2π/12, то есть 30°. Середины интервалов, соответствующих каждому месяцу начиная с января, приведены в графе 3 табл. III.2.

Таблица III.2. Проверка гипотезы о равномерном распределении случаев оползания бортов карьера в течение года

Месяц	Количество случаев оползания пi,	Средняя точка ,	sin	пi sin	cos	пi cos
1	2	3	4	5	6	7
I	0	15	0,2588	0	0,9659	0
II	0	45	0,7071	0	0,7071	0
III	3	75	0,9659	2,8978	0,2588	0,7765
IV	6	105	0,9659	5,7956	-0,259	-1,553
V	2	135	0,7071	1,4142	-0,707	-1,414
VI	1	165	0,2588	0,2588	-0,966	-0,966
VII	2	195	-0,259	-0,518	-0,966	-1,932
VIII	1	225	-0,707	-0,707	-0,707	-0,707
IX	2	255	-0,966	-1,932	-0,259	-0,518
X	0	285	-0,966	0	0,2588	0
XI	2	315	-0,707	-1,414	0,7071	1,4142
XII	0	345	-0,259	0	0,9659	0
Σ	19			5,7956		-4,899

.

Выполнив необходимые расчеты (табл. III.2, графы 4 – 7), получили, что = 0,399 и превышает критическое значение = 0,394 для n =19 и α=0,05 (приложение IV). Таким образом, гипотеза о равномерном распределении случаев оползания бортов карьера в течение года отвергается. Следовательно, нет оснований отрицать возможность сезонного изменения устойчивости бортов карьера.

Вычисления можно организовать так, как это показано на рис. III.15.

Рис. III.15. Проверка гипотезы о равномерном распределении угловой величины

ЗАДАЧА III.3

Для распределения Мизеса плотность распределения вероятностей выражается формулой

при и k > 0, где

Распределение Мизеса, так же как и нормальное распределение, определяется двумя параметрами – μ и k. Причем μ – круговое среднее направление случайной угловой величины – схоже с математическим ожиданием Mx, а параметр k можно рассматривать как характеристику концентрации распределения около μ. Распределение Мизеса при k=0 превращается в равномерное, а при , с параметрами μ и k оно асимптотически ведет себя как нормальное с параметрами Mx=μ и σ² = 1/k. Таким образом, параметр 1/k в распределении Мизеса играет ту же роль, что и дисперсия в случае нормального распределения.

Требуется

Проверить гипотезы о соответствии распределения случайной угловой величины распределению Мизеса.

Указание

Выборочные значения случайной угловой величины группируются в класс-интервалы так, чтобы для большинства классов количество замеров составляло не менее 2 – 5.

По выборочным данным с помощью формул (II.1), (II.2) рассчитываются оценки т и . Оценка параметра используется для нахождения по специальным таблицам (приложение V) оценки параметра концентрации k распределения Мизеса. Получив оценки μ и k по таблицам распределения Мизеса (приложение VI) можно найти теоретические вероятности, соответствующие границам класс-интервалов. Таблицы Мизеса составлены для распределения с параметрами μ =180° и k=0; 0,2; ...; 10. Поэтому значения изучаемой угловой величины необходимо центрировать, то есть как бы «сдвинуть» на величину 180° – m или m – 180°, чтобы выборочное угловое среднее направление т совпало с направлением 180°. Для упрощения пользования таблицей Мизеса выборочные данные целесообразно перегруппировать таким образом, чтобы выборочное значение m совпало с границей одного из класс-интервалов.

Теоретическая вероятность попадания случайной угловой величины в каждый класс-интервал определяется как разница между вероятностями, соответствующими верхней и нижней границам данного класс-интервала: , а теоретическая частота рассчитывается путем умножения на объем выборки:

(III.3)

Проверка гипотезы о соответствии выборочных данных распределению Мизеса производится путем сравнения теоретических и фактических частот по критерию Пирсона χ² при числе степеней свободы K = k – 3, где k – число классов группирования.

В табл. III.3 приведены замеры азимутов падения кварцевых прожилков по документации канав на рудопроявлении золота. Количество замеров невелико, поэтому ширину класс-интервалов при группировании целесообразно принять равной 20°. По сгруппированным данным с помощью расчетов (табл. III.4) найдено, что выборочное среднее направление азимутов падения прожилков равно 173,5°. По приложению V имеем, что для =0,33 оценка параметра концентрации k равна 0,7. В таблице Мизеса значения параметра k приведены с точностью до 0,1, поэтому вычислять оценку k с большой точностью нецелесообразно.

Таблица III.3. Замеры азимутов (в градусах) падения кварцевых прожилков

№ п/п	Азимут	№ п/п	Азимут	№ п/п	Азимут	№ п/п	Азимут
1	132	13	330	25	178	37	105
2	302	14	88	26	335	38	130
3	304	15	191	27	110	39	144
4	162	16	198	28	112	40	177
5	130	17	325	29	200	41	42
6	58	18	214	30	257	42	190
7	159	19	211	31	270	43	169
8	144	20	199	32	171	44	41
9	315	21	124	33	141	45	205
10	162	22	84	34	260	46	225
11	318	23	181	35	185	47	270
12	92	24	3	36	15	48	260

Таблица III.4. Оценка параметров m и азимутов падения кварцевых прожилков

Азимут, градусы	Частота пi,	Средний азимут	sin	пi sin	cos	пi cos
1	2	3	4	5	6	7
0–20	2	10	0,174	0,348	0,985	1,970
20–40	0	30	0	0	0	0
40–60	3	50	0,766	2,298	0,643	1,929
60–80	0	70	0	0	0	0
80–100	3	90	1,000	3,000	0	0
100–120	3	110	0,940	2,820	-0,342	-1,026
120–140	4	130	0,766	3,064	-0,643	-2,572
140–160	4	150	0,500	2,000	-0,866	-3,464
160–180	6	170	0,174	1,044	-0,985	-5,910
180–200	7	190	-0,174	-1,218	-0,985	-6,895
200–220	3	210	-0,500	-1,500	-0,866	-2,598
220–240	1	230	-0,766	-0,766	-0,643	-0,643
240–260	3	250	-0,940	-2,820	-0,342	-1,026
260–280	2	270	-1,000	-2,000	0	0
280–300	0	290	0	0	0	0
300–320	4	310	-0,766	-3,064	0,643	2,572
320–340	3	330	-0,500	-1,500	0,866	2,598
340–360	0	350	0	0	0	0
Σ	48			1,706		-15,065

Для упрощения дальнейших расчетов границы класс-интервалов смещаются таким образом, чтобы одна из них совпадала со средним круговым направлением, то есть с 173,5° (табл. III.5, графа 1), и определяются частоты для новых класс-интервалов (табл. III.5, графа 2). Для нахождения по приложению VI теоретических вероятностей р_i попадания замеров азимутов в каждый класс-интервал следует сдвинуть границы этих интервалов на 180° – 173,5° = 6,5°, чтобы выборочное среднее направление (173,5°) совпало со средним направлением теоретического распределения Мизеса.

Таблица III.5. Проверка гипотезы о соответствии распределения азимутов (в градусах) падения кварцевых прожилков распределения Мизеса

Азимут θ	ni	Азимут θ + (180° – m)	pi		ni		ni –
1	2	3	4	5	6	7	8	9
353,5–13,5	1	0 – 20	0,025	1,20	5	5,904	-0,904	0,138417
13,5–33,5	1	20 – 40	0,027	1,30
33,5–53,5	2	40 – 60	0,032	1,54
53,5–73,5	1	60 – 80	0,039	1,87
73,5–93,5	3	80 – 100	0,049	2,35	6	5,376	0,624	0,072429
93,5–113,5	3	100 – 120	0,063	3,02
113,5–133,5	4	120 – 140	0,077	3,70	7	8,016	-1,016	0,128774
133,5–153,5	3	140 – 160	0,090	4,32
153,5–173,5	5	160 – 180	0,098	4,70	5	4,704	0,296	0,018626
173,5–193,5	6	180 – 200	0,098	4,70	6	4,704	1,296	0,357061
193,5–213,5	5	200 – 220	0,090	4,32	7	8,016	-1,016	0,128774
213,5–233,5	2	220 – 240	0,077	3,70
233,5–253,5	–	240 – 260	0,063	3,02	5	5,376	-0,376	0,026298
253,5–273,5	5	260 – 280	0,049	2,35
273,5–293,5	–	280 – 300	0,039	1,87	7
293,5-313,5	2	300 – 320	0,032	1,54
313,5–333,5	4	320 – 340	0,027	1,30
333,5–353,5	1	340 – 360	0,025	1,20
Σ	48		1	48	48	48	0	1,074

Значения теоретических вероятностей р_i находят по разности значений распределения Мизеса для верхней и нижней границ класса.

Например, при концентрации k равной 0,7 для класса-интервала 13,5° – 33,5° по приложению VI приблизительно имеем значения функции распределения Мизеса: для верхней границы 33,5° – 0,045 и нижней границы 13,5° – 0,018. Таким образом, теоретическая вероятность равна разности значений распределения Мизеса для верхней и нижней границ класса 0,045–0,018=0,027.

Так как распределение Мизеса симметрично относительно среднего направления, в приложении VI вероятности приведены только для интервала 0° – 180°. Теоретические вероятности для углов θ больше 180° равны вероятности для углов 360° – θ.

В связи с тем, что рассчитанные по формуле (III.3) теоретические чистоты , в данном примере для большинства классов, оказались меньше 5 (см. табл. III.5, графа 5), ширину класс-интервалов для дальнейших расчетов целесообразно увеличить, просуммировав значения теоретических и фактических частот по соседним классам (см. табл. III.5, графа 6 и 7).

Число класс-интервалов после их объединения равно 8, поэтому полученное значение критерия χ² = 1,074 сравнивается с табличными для числа степеней свободы, равного 5. По приложению III критическое значение критерия χ² при K=5 и доверительной вероятности 0,95 равно 1,15. Следовательно, гипотеза о соответствии распределения азимутов падения прожилков закону Мизеса не отвергается. Критическое значение критерия χ² может быть также вычислено с помощью функции пакета Excel ХИ2ОБР. Соответствие данных заданному закону распределения можно определить также с помощью функции ХИ2ТЕСТ. Размещение расчетов на рабочем листе электронных таблиц Excel и порядок расчетов задачи – см. рис. III.16.

Рис. III.16. Фрагмент решения с использованием критерия Мизеса

ПРОВЕРКА ГИПОТЕЗ О РАВЕНСТВЕ СРЕДНИХ (МАТЕМАТИЧЕСКИХ ОЖИДАНИЙ)

Выявление достоверности различий. Следующей задачей статистического анализа, решаемой после определения основных выборочных характеристик и анализа одной выборки, является совместный анализ нескольких выборок. Важнейшим вопросом, возникающим при анализе двух выборок, является вопрос о наличии различий между этими выборками. Обычно для этого проводят проверку статистических гипотез о принадлежности обеих выборок одной генеральной совокупности или о равенстве генеральных средних. Для решения задач такого типа используются так называемые критерии различия. Для проверки одной и той же гипотезы могут быть использованы разные статистические критерии. Правильный выбор критерия определяется как спецификой данных и проверяемых гипотез, так и уровнем статистической подготовки исследователя.

Необходимость сравнения средних значений изучаемых свойств геологических объектов возникает при решении широкого круга задач во всех отраслях геологических наук. Так, например, по мнению многих петрологов, средний химический состав лав вулканов и интрузивных пород отражает в общих чертах особенности состава породивших их глубинных магматических очагов. Путем сравнения различных эффузивных и интрузивных пород по среднему содержанию в них химических элементов можно судить о комагматичности (то есть генетическом родстве) эффузивных и интрузивных образований, о принадлежности интрузивных образований к определенному магматическому комплексу или двух вулканических построек к одному глубинному магматическому очагу.

Известно, что метаморфические породы характеризуются устойчивыми парагенетическими ассоциациями с небольшим (2–4) числом породообразующих минералов. Различия в наборе и процентных соотношениях этих минералов отражают различия в химическом составе исходных пород, претерпевших метаморфизм. Статистические методы проверки гипотезы о равенстве средних содержаний породообразующих минералов используются для стратиграфического расчленения метаморфических комплексов и корреляции их разрезов при детальном геологическом картировании.

В палеонтологии статистические методы проверки гипотезы о равенстве средних способствуют объективному разделению семейств ископаемых организмов на виды. Для выделения нового вида необходимо доказать, что данная группа ископаемых организмов существенно отличается по среднему значению какого-либо морфологического признака, например, по степени сферичности или углу между линиями замкового шва и краем вентрального синуса.

В процессе разведки месторождения о надежности выбранного способа отбора проб обычно судят по контрольным пробам, которые отбираются другим, более надежным способом, но, как правило, более трудоемким и дорогим. Проверка гипотезы о равенстве средних содержаний полезного компонента, рассчитанных по рядовым и контрольным пробам, позволяет объективно решить вопрос о наличии или отсутствии систематических ошибок в результатах рядового опробования. Число подобных примеров можно было бы увеличить. Общим во всех перечисленных случаях является невозможность уверенного решения задач такого типа путем визуального сравнения средних значений свойств, так как эти свойства характеризуются большой изменчивостью, а объем выборок часто бывает невелик. Как правило, выборочные оценки средних обладают значительными дисперсиями и могут заметно различаться даже для совершенно аналогичных объектов.

Для решения перечисленных задач используются параметрические и непараметрические критерии согласия.

Параметрические критерии. Параметрические критерии служат для проверки гипотез о положении и рассеивании. Из параметрических критериев наибольшей популярностью при проверке гипотез о равенстве генеральных средних (математических ожиданий) пользуется t-критерий Стьюдента (t-критерий различия). Критерий Стьюдента наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности». Критерий позволяет найти вероятность того, что оба средних относятся к одной и той же совокупности. Если эта вероятность р ниже уровня значимости (р < 0,05), то принято считать, что выборки относятся к двум разным совокупностям.

При использовании t-критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и опытная группа. Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными.

В обоих случаях в принципе должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп и равенства дисперсий в сравниваемых совокупностях. Однако на практике по большому счету корректное применение t-критерия Стьюдента для двух групп часто бывает затруднительно, поскольку достоверно проверить эти условия удается далеко не всегда.

Для оценки достоверности отличий по критерию Стьюдента принимается нулевая гипотеза, что средние выборок равны между собой. Затем вычисляется значение вероятности того, что изучаемые события (например, количества реализованных путевок в обеих выборках) произошли случайным образом.

В Excel для оценки достоверности отличий по критерию Стьюдента используются специальная функция ТТЕСТ и процедуры пакета анализа.

Все перечисленные инструменты вычисляют вероятность, соответствующую критерию Стьюдента, и используются, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.

Функция ТТЕСТ использует следующие параметры: ТТЕСТ(массив1;массив2;хвосты;тип). Здесь:

• массив 1 – это первое множество данных;

• массив2 – это второе множество данных;

• хвосты – число хвостов распределения. Обычно число хвостов равно 2; если хвосты = 1, то функция ТТЕСТ использует одностороннее распределение. Если хвосты = 2, то функция ТТЕСТ использует двустороннее распределение.

• тип – это вид исполняемого t-теста. Возможны 3 варианта выбора: 1 – парный тест, 2 – двухвыборочный тест с равными дисперсиями, 3 – двухвыборочный тест с неравными дисперсиями.

ПРИМЕР III.4

Требуется

Сравнить интрузии 1 и 2 – см. табл. III.6 и III.7. Выявить, достоверны ли отличия при сравнении данных геохимических проб по содержанию: 1) оксида Na₂O; 2) оксида K₂O.

Так как химический состав каждой интрузии определялся по совокупности геохимических проб (то есть по выборочным данным), объективно вопрос о сходстве или различии интрузий может быть решен только с помощью статистических критериев согласия. Отсюда необходимо получить оценки средних значений для содержания каждого оксида в интрузиях 1 и 2.

Решение

1. Введите данные: в ячейки A2:A81 – содержание оксида Na₂O (в %) для интрузии 1, в ячейки D2:D81 – содержание оксида Na₂O (в %) для интрузии 2, в ячейки B2:B81 – содержание оксида K₂O (в %) для интрузии 1, в ячейки E2:E81 – содержание оксида K₂O (в %) для интрузии 2.

Таблица III.6. Содержание оксидов (в %) по данным опробования 1 гранитной интрузии

№ п/п	Na2O	K2O	№ п/п	Na2O	K2O
1	2,40	3,60	41	4,32	3,36
2	2,31	3,75	42	2,91	3,01
3	6,99	3,30	43	4,90	3,11
4	6,24	4,46	44	5,03	4,30
5	5,36	2,84	45	2,70	2,43
6	4,06	1,42	46	3,34	1,82
7	5,51	3,52	47	5,31	2,48
8	3,63	2,10	48	3,57	3,84
9	4,14	3,41	49	4,01	3,58
10	3,96	3,30	50	1,49	2,57
11	3,30	1,44	51	3,55	2,86
12	5,32	4,38	52	3,67	2,27
13	1,08	1,15	53	3,40	4,05
14	4,35	4,97	54	4,38	5,04
15	2,96	2,07	55	4,39	3,12
16	3,57	3,71	56	4,53	1,38
17	3,68	3,20	57	4,34	4,38
18	4,92	0,95	58	2,65	2,61
19	4,47	1,26	59	5,12	3,65
20	5,00	3,86	60	4,70	2,71
21	2,68	2,79	61	2,83	3,19
22	4,74	4,42	62	4,26	3,78
23	3,08	2,88	63	3,48	3,19
24	3,01	2,75	64	3,72	2,74
25	3,34	1,37	65	5,55	4,58
26	4,26	2,88	66	4,59	4,09
27	3,16	1,86	67	4,34	3,45
28	3,35	1,67	68	3,22	2,54
29	4,21	1,60	69	2,82	3,96
30	4,14	2,87	70	4,90	2,51
31	2,04	2,90	71	5,08	3,22
32	3,69	3,42	72	3,80	2,68
33	5,30	3,60	73	4,62	4,10
34	3,00	3,24	74	4,67	4,21
35	3,94	4,22	75	3,45	2,85
36	3,46	2,54	76	4,91	1,30
37	3,23	4,29	77	3,22	1,96
38	3,32	3,54	78	4,31	4,62
39	4,41	1,34	79	5,16	4,05
40	2,79	3,66	80	3,34	3,09

Таблица III.7.Содержание оксидов (в %) по данным опробования 2 гранитной интрузии

№ п/п	Na2O	K2O	№ п/п	Na2O	K2O
1	4,34	3,73	41	5,00	1,81
2	4,82	4,16	42	2,98	4,30
3	5,13	2,50	43	4,09	1,81
4	3,34	4,01	44	3,24	2,34
5	4,64	5,88	45	4,12	4,19
6	2,56	3,20	46	4,48	3,41
7	4,00	1,73	47	2,51	3,16
8	5,42	4,26	48	4,06	2,37
9	3,46	2,72	49	4,25	3,75
10	5,24	4,71	50	3,62	2,78
11	3,33	3,58	51	4,35	1,47
12	4,44	3,24	52	3,71	1,02
13	4,83	3,08	53	3,12	3,78
14	5,30	2,15	54	3,94	3,31
15	2,90	2,50	55	4,76	3,48
16	3,54	3,44	56	5,44	0,43
17	2,11	1,12	57	4,84	2,61
18	4,14	2,75	58	4,63	0,17
19	4,63	2,68	59	3,56	3,36
20	4,69	3,86	60	2,78	1,26
21	4,29	2,74	61	2,99	2,91
22	3,95	0,17	62	4,88	3,08
23	3,04	3,95	63	5,02	2,62
24	3,92	2,03	64	3,16	2,10
25	4,02	1,31	65	6,20	2,66
26	3,90	2,44	66	5,30	3,51
27	5,30	2,37	67	3,09	3,00
28	3,86	1,89	68	2,41	1,72
29	4,04	1,27	69	4,28	1,31
30	3,16	3,52	70	3,27	2,01
31	4,86	2,43	71	3,55	1,64
32	4,08	3,47	72	4,34	2,18
33	3,16	2,69	73	3,34	2,85
34	4,80	3,60	74	3,59	2,17
35	5,22	2,78	75	4,28	2,19
36	4,69	3,74	76	4,90	1,66
37	3,00	0,98	77	4,80	3,50
38	2,08	2,36	78	4,84	2,68
39	5,00	2,30	79	2,84	2,57
40	2,64	3,48	80	2,78	4,05

2. Для выявления достоверности отличий по содержанию оксида Na₂O (в %) табличный курсор установите в свободную ячейку (C85). На панели инструментов необходимо нажать кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ТТЕСТ, после чего нажмите кнопку OK. Появившееся диалоговое окно ТТЕСТ за серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы в поле Массив 1 (A2:A81). В поле Массив 2 введите диапазон данных исследуемой группы (D2:D81). В поле Хвосты введите с клавиатуры цифру 2, а в поле Тип с клавиатуры введите цифру 3. Нажмите кнопку OK. В ячейке C85 появится значение вероятности – 0,612.

3. Для выявления достоверности отличий по содержанию оксида K₂O (в %) табличный курсор установите в свободную ячейку (C86). На панели инструментов необходимо нажать кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ТТЕСТ, после чего нажмите кнопку OK. Появившееся диалоговое окно ТТЕСТ за серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы в поле Массив 1 (B2:B81). В поле Массив 2 введите диапазон данных исследуемой группы (E2:E81). В поле Хвосты введите с клавиатуры цифру 2, а в поле Тип с клавиатуры введите цифру 3. Нажмите кнопку OK. В ячейке C86 появится значение вероятности – 0,025.

4. Поскольку величина вероятности случайного появления анализируемых выборок по содержанию оксида Na₂O (0,612) больше уровня значимости (α = 0,05), то нулевая гипотеза не отвергается. Следовательно, различия между выборками случайные и средние выборок считаются достоверно не отличающимися друг от друга.

Величина вероятности случайного появления анализируемых выборок по содержанию оксида K₂O (0,025) меньше уровня значимости (α = 0,05), то нулевая гипотеза отвергается. Следовательно, различия между выборками случайные и средние выборок считаются достоверно отличающимися друг от друга.

ЗАДАЧА III.4

Как указывалось выше, при использовании t-критерия выделяют два основных случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть две различных выборки, количество элементов в которых может быть также различно. При заполнении диалогового окна ТТЕСТ при этом указывается Тип 3.

Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными (при заполнении диалогового окна ТТЕСТ указывается Тип 1).

Требуется

Рассмотреть пример по данным геохимических проб по содержанию оксида Na₂O и оксида K₂O. Определить достоверность различия между группами при двух вариантах постановки задачи:

• группы состоят из различных интрузий (тип 3) – см. табл. III.6 и III.7;

• две группы составлены по итогам исследования одной и той же интрузии: первая – составлена по предварительным исследованиям, а вторая – по результатам – полученным позже (тип 1) – см. табл. III.6 и III.8.

Таблица III.8. Содержание оксидов (в %) по данным вторичного опробования 1 гранитной интрузии

№ п/п	Na2O	K2O	№ п/п	Na2O	K2O
1	3,12	3,78	41	2,73	2,29
2	2,76	3,34	42	3,90	3,84
3	2,13	4,71	43	1,57	4,32
4	1,98	5,15	44	4,33	4,63
5	3,42	4,16	45	2,75	2,84
6	3,06	3,46	46	2,60	4,14
7	3,56	4,18	47	3,34	2,06
8	0,64	4,97	48	3,82	3,50
9	4,96	4,02	49	4,38	4,92
10	2,72	5,14	50	2,64	2,96
11	3,93	2,62	51	3,08	4,74
12	1,97	3,14	52	3,13	2,83
13	3,48	5,09	53	2,76	3,94
14	5,71	3,60	54	2,12	4,33
15	2,94	4,18	55	3,47	4,80
16	2,70	2,42	56	3,04	2,43
17	2,61	3,82	57	4,42	3,04
18	1,95	3,87	58	1,97	1,61
19	1,65	2,80	59	4,81	3,64
20	4,00	4,02	60	2,42	3,96
21	1,98	3,78	61	3,44	4,19
22	3,55	4,89	62	2,15	3,79
23	3,42	3,91	63	3,49	3,45
24	3,07	3,56	64	3,68	2,54
25	3,52	2,56	65	1,78	4,42
26	3,48	4,01	66	3,89	3,52
27	3,83	2,09	67	2,22	3,41
28	4,11	2,65	68	2,81	4,80
29	4,27	2,31	69	2,07	3,36
30	3,23	3,68	70	1,42	3,53
31	2,70	3,41	71	3,08	2,66
32	4,06	2,63	72	4,60	3,66
33	3,16	2,76	73	0,10	3,56
34	2,87	3,91	74	4,12	4,72
35	1,80	3,37	75	4,21	4,19
36	4,70	3,13	76	4,17	2,50
37	2,09	3,50	77	3,28	1,58
38	4,22	2,82	78	3,04	4,14
39	1,35	3,92	79	3,11	3,34
40	4,30	4,29	80	3,20	1,26

ИСПОЛЬЗОВАНИЕ ИНСТРУМЕНТА ПАКЕТ АНАЛИЗА ДЛЯ ВЫЯВЛЕНИЯ РАЗЛИЧИЙ МЕЖДУ ВЫБОРКАМИ

Для анализа двух выборок с помощью t-теста Стьюдента могут быть использованы следующие процедуры: Парный двухвыборочный t-тест для средних; Двухвыборочный t-тест с одинаковыми дисперсиями и Двухвыборочный t-тест с различными дисперсиями. В общем случае необходимо воспользоваться процедурой Двухвыборочный t-тест с различными дисперсиями, так как процедуры Парный двухвыборочный t-тест для средних и Двухвыборочный t-тест с одинаковыми дисперсиями относятся к частным, специальным случаям.

Для выполнения процедуры анализа необходимо:

• выполнить команду Сервис/Анализ данных;

• в появившемся списке Инструменты анализа выбрать строку Двухвыборочный t-тест с различными дисперсиями, щелкнуть левой кнопкой мыши и нажать кнопку OK;

• в появившемся диалоговом окне указать Интервал переменной 1, то есть ввести ссылку на первый диапазон анализируемых данных, содержащий один столбец данных. Для этого следует навести указатель мыши на верхнюю ячейку первого столбца данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

• указать Интервал переменной 2, то есть ввести ссылку на второй диапазон анализируемых данных, содержащий один столбец данных. Для этого следует навести указатель мыши в поле ввода Интервал переменной 2 и щелкнуть левой кнопкой мыши, затем навести указатель мыши на верхнюю ячейку второго столбца данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

• указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить флажок в левое поле Выходной диапазон (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные.

• нажать кнопку OK.

Результаты анализа. В выходной диапазон будут выведены: средняя, дисперсия и число наблюдений для каждой переменной, гипотетическая разность средних, df (число степеней свободы), значение t-статистики, Р(Т <= t) одностороннее, t критическое одностороннее, Р(Т <= t) двухстороннее, t критическое двухстороннее.

Интерпретация результатов. Если величина вероятности случайного появления анализируемых выборок (Р(Т <= t) двухстороннее) меньше уровня значимости (α = 0,05). принято считать, что различия между выборками не случайные, то есть различия достоверные.

ЗАДАЧА III.5

Требуется

По условию ПРИМЕРА III.4 (см. табл. III.6 и III.7), решить, используя пакет анализа, задачу о равенстве средних при сравнении данных геохимических проб по содержанию: 1) оксида Na₂O; 2) оксида K₂O.

Указание

Выбор процедуры осуществляется из трех вариантов t-теста. Поскольку данные не имеют попарного соответствия, и говорить о равенстве дисперсий затруднительно, выберите процедуру Двухвыборочный t-тест с различными дисперсиями.

Итак, наиболее часто для проверки гипотезы о равенстве средних в геологической практике употребляется параметрический критерий Стьюдента t. Его применение основано на том, что если из нормально распределенной совокупности отобраны выборки X₁, X₂, ..., X_k объемом в п₁ значений и выборки Y₁, Y₂, ..., Y_k объемом в п₂ значений, то величина

, (III.4)

где , – выборочные оценки среднего, a , – выборочные оценки дисперсии, подчиняется закону распределения Стьюдента с п₁+п₂–2 степенями свободы. Проверка гипотезы о равенстве двух выборочных средних заключается в подстановке в формулу (III.4) оценок и по первой и и по второй выборке и сравнении полученного значения критерия t с табличным для данного числа степеней свободы и заданной доверительной вероятности. Если расчетное значение критерия превышает табличное, то гипотеза о равенстве выборочных средних отвергается.

В случае соответствия выборочных данных логнормальной модели для проверки гипотезы о равенстве средних рекомендуется использовать критерий Родионова. Д.А. Родионовым было установлено, что величина

(III.5)

распределена асимптотически нормально с математическим ожиданием 0 и дисперсией 1. Поэтому при проверке гипотезы о равенстве средних с помощью этого критерия теоретическое значение величины Z находим по таблице значений интегральной функции Лапласа (см. приложение I).

В некоторых геологических задачах, например при проверке гипотезы о комагматичности пород, гипотезу о равенстве математических ожиданий можно заменить гипотезой о равенстве центров распределения, то есть медиан. В этом случае можно воспользоваться критерием Стьюдента даже при логнормальном распределении изучаемых величин, использовав оценки средних значений и дисперсий логарифмов:

.

ЗАДАЧА III.6

В районе широко развиты интрузии гранитов средне- и поздне-палеозойского возраста. Со среднепалеозойскими гранитами связаны месторождения редкометалльных пегматитов. Среднепалеозойские граниты отличаются от нерудоносных верхнепалеозойских повышенным содержанием Na₂O и Тi₂O и пониженным содержанием K₂О (табл. III.9). Распределение содержаний Na₂O и K₂О в гранитах обоих комплексов соответствует нормальном закону, а содержание Тi₂O – логнормальному.

Требуется

Использовать эти различия для определения возраста интрузии и оценки перспектив их рудоносности и тех случаях, когда эту задачу нельзя решить по возрастным взаимоотношениям гранитов и осадочных пород.

Таблица III.9. Исходные даяние оценки рудоносности гранитов неизвестного возраста (в %)

Возраст гранитов	Число проб	Na2O		K2О		Тi2O
Средний палеозой	100	3,90	1,21	4,51	1,42	-0,886	0,268
Поздний палеозой	100	3,46	1,52	5,02	1,65	-1,426	0,321
Неизвестен	30	3,38	1,83	4,83	1,88	-1,352	0,225

Указание

В нижней строке табл. III.9 приведены числовые характеристики содержания оксидов по одной из интрузий неизвестного возраста. Ее сопоставление с интрузиями определенного возраста по содержанию Na₂O и K₂О можно провести с помощью критерия Стьюдента, а по содержанию Тi₂O с помощью критерия Родионова.

В данной задаче проверяемая гипотеза Н₀ состоит в том, что и равны, то есть , при альтернативе , то есть или . Поэтому уровень значимости α принимается для двусторонних критериев t_α и .

При сравнении интрузий неизвестного возраста с рудоносными среднепалеозойскими гранитами ошибка первого рода будет состоять в том, что фактически перспективная интрузия того же возраста будет признана нерудоносной, и поисковые работы на этом участке будут прекращены, что может привести к пропуску месторождения. Ошибка второго рода произойдет, если фактически нерудоносная интрузия другого возраста будет отнесена к рудоносному комплексу, поисковые работы будут продолжены, но не дадут положительного результата. Экономический ущерб от этой ошибки в данном случае заключается в непроизводительных затратах на поисковые работы в пределах оцениваемой локальной площади. Определить ущерб от ошибки первого рода сложнее, но он может быть гораздо значительнее, так как пропуск месторождения обычно можно восполнить только путем изучения гораздо больших по площади территорий в другом районе. Поэтому при проверке данной гипотезы уровень значимости, то есть вероятность ошибки первого рода, целесообразно принять довольно низким – 0,05, несмотря на то, что при этом увеличивается вероятность ошибки второго рода.

Сравнивая ту же интрузию с заведомо нерудоносными верхнепалеозойскими гранитами, наоборот следует стремиться снизить вероятность ошибки второго рода. Поэтому уровень значимости целесообразно увеличить до 0,1.

Сравнение интрузий неизвестного возраста со среднепалеозойскими гранитами производится по формулам (III.4) и (III.5):

по Na₂O ;

по K₂О ;

по Тi₂O .

Для уровня значимости α = 0,05 критическое значение критерия Стьюдента при числе степеней свободы п₁+п₂–2 =128 равно 1,98 (см. приложение II).

Таким образом, гипотеза об идентичности средних содержаний Na₂O отвергается, в то время как различие по содержанию K₂О можно признать несущественным. Критическое значение Z для тех же условий равно 1,96 (см. приложение I), поэтому гипотеза о равенстве содержаний также отвергается. Последняя гипотеза отвергается даже в том случае если уровень значимости снизить до 0,001 ( ).

Критическое значение Z может быть найдено с помощью формулы =НОРМСТОБР(0,025).

Сравнение гранитов неизвестного возраста с верхнепалеозойскими гранитами производится по формулам (III.4) и (III.5):

по Na₂O ;

по K₂О ;

по Тi₂O .

Критическое значение критерия Стьюдента (t) и критерия Z для уровня значимости α = 0,1 равны: (см. приложения I и II).

Поэтому гипотеза об идентичности химического состава изучаемой интрузии с верхнепалеозойскими гранитами принимается для всех трех компонентов.

По совокупности проверенных гипотез можно достаточно уверенно дать отрицательную оценку перспектив рудоносности в пределах данной интрузии.

Вычисления следует организовать в электронных таблицах Excel. Для вычисления модуля числа используйте формулу =ABS(число), которая возвращает модуль (абсолютную величину) числа. Абсолютная величина числа – это число без знака.

Непараметрические критерии (критерий Ван-дер-Вардена, Вилкоксона, критерий согласия χ²) используются обычно при малом объеме выборок или в тех случаях, когда средние значения рассчитаны по полуколичественным данным – например по результатам полуколичественного спектрального анализа. Непараметрические критерии используются в тех случаях, когда закон распределения данных отличается от нормального или неизвестен.

Проверка гипотезы о равенстве средних, определенных по двум выборкам (А и Б) с помощью X-критерия Ван-дер-Вардена, начинается с того, что все значения по обеим выборкам ранжируются, то есть записываются в один ряд в порядке возрастания. X-критерий представляет собой величину

,

где п – общее число значений по двум выборкам; h – число наблюдений в выборке ; i – порядковый номер каждого значения выборки Б в общем ряду; ψ(...) – функция, обратная функции нормального распределения.

При п>20 величина Х распределена асимптотически нормально с математическим ожиданием 0 и дисперсией . Процедура проверки гипотезы сводится к расчету всех значений аргумента i/(n+1), нахождению по таблицам обратной функции нормального распределения значений функции ψ для этих аргументов, суммированию значений функции ψ и сравнению полученного значения критерия Х с табличным для заданного уровня значимости, общего числа наблюдений п и разницы между объемами выборок А и Б. Если расчетное значение Х по абсолютной величине больше табличного, гипотеза о равенстве выборочных средних отвергается.

Для функции ψ(...) существуют специальные таблицы. Однако ее значения можно найти и с помощью обычных таблиц интегральной функции нормального распределения с параметрами 0,1 (см. приложение I), используя ее в обратном порядке. При этом значения аргумента i/(n+1) приравниваются к вероятностям р, а величина ψ(i/(n+1)) находится по значениям Z, соответствующим этим вероятностям.

Для i/(n+1) значения ψ(i/(n+1)) будут отрицательными, а для i/(n+1) > 0,5 – положительными.

Вместо обычных таблиц интегральной функции нормального распределения можно воспользоваться функцией Excel НОРМСТОБР.

Если систематических расхождений между выборками А и Б нет, то в ранжированном ряду значения каждой выборки будут располагаться симметрично относительно середины этого ряда, соответствующей i=n/2 и i/(n+1) = 0,5, число отрицательных и положительных значений ψ(i/(n+1)) для каждой выборки будет примерно равным, а их алгебраические суммы, то есть значения X-критерия, близки к нулю.

ПРИМЕР III.5

Требуется

Для снижения затрат на разведку на одном из участков россыпного месторождения золота часть шурфов (примерно каждый второй) была заменена скважинами ударно-канатного бурения. Необходимо убедиться в том, что результаты опробования скважин не имеют систематической ошибки. Так как число скважин и шурфов на опытном участке невелико – 13 и 10, для сопоставления вычисленных по ним содержаний золота можно использовать непараметрический критерий Ван-дер-Вардена. Результаты опробования шурфов и скважин приведены в табл. III.10. По этим данным составлен общий вариационный ряд (табл. III.11).

Таблица III.10. Результаты опробования разведочных выработок на россыпном месторождении золота

Выработка А (скважины)		Выработка А (скважины)		Выработка Б (шурфы)		Выработка Б (шурфы)
№п/п	Содержание Au, м2/м3	№ п/п	Содержание Au, м2/м3	№п/п	Содержание Au, мг/м3	№ п/п	Содержание Au, мг/м3
1	322	7	192	1	431	6	221
2	250	8	375	2	397	7	548
3	225	9	381	3	462	8	478
4	315	10	538	4	457	9	299
5	399	11	198	5	251	10	541
6	348	12	317
		13	293

Проверяемая гипотеза Н₀ в данной задаче заключается в том, что систематических расхождений в определении содержаний золота по шурфам и скважинам нет (то есть Н₀: Х=0, А=Б), при альтернативе Н₁: Х≠0, А≠Б (то есть А>Б или А<Б). Поэтому для нахождения критического значения Х нужно воспользоваться таблицами двустороннего критерия Ван-дер-Вардена (см. приложение VII).

Таблица III.11. Проверка гипотезы о равенстве средних содержаний золота по критерию Ван-дер-Вардена

№ п/п	Содержание	Выборка	i/(n+1)	ψ(i/(n+1))
1	192	А
2	198	А
3	221	Б	0,125	-1,15
4	225	А
5	250	А
6	251	Б	0,250	-0,67
7	293	А
8	299	Б	0,333	-0,43
9	315	А
10	317	А
11	322	А
12	348	А
13	375	А
14	381	А
15	397	Б	0,625	0,32
16	399	А
17	431	Б	0,708	0,55
18	457	Б	0,750	0,67
19	462	Б	0,792	0,81
20	478	Б	0,833	0,97
21	538	А
22	541	Б	0,917	1,39
23	548	Б	0,958	1,73

Х=4,19

Ошибка первого рода в данной задаче заключается в том, что правильная гипотеза об отсутствии систематического расхождения между результатами опробования шурфов и скважин будет отвергнута, а это не позволит снизить затраты на дальнейшую разведку за счет использования более дешевых скважин. Ошибка второго рода, то есть принятие неверной гипотезы Н₀, состоит в признании несущественным (случайным) расхождения между данными по шурфам и скважинам, в то время как на самом деле оно носит систематический характер. Ошибка второго рода в данной ситуации может привести к неправильной геолого-экономической оценке месторождения, что нанесет гораздо больший экономический ущерб по сравнению с дополнительными затратами за счет ошибки первого рода. Поэтому для уменьшения риска ошибки второго рода уровень значимости при проверке гипотезы Н₀ целесообразно принять не слишком высоким, например 0,1.

Решение

В столбец B введите значения порядковых номеров скважины А: от 1 до 13 (ячейки B1:B13), в столбец C – содержание Au (м²/м³ ) скважины А (ячейки C1:C13) – см. табл. III.11, затем значения порядковых номеров скважины Б: от 1 до 10 (ячейки B14:B23), в столбец C – содержание Au (м²/м³ ) скважины Б (ячейки C14:C23) – см. табл. III.11. В ячейки A1:A13 введите символ А, в ячейки A14:A23 – символ Б. Выделите диапазон A1:C23 и через пункт меню Данные/Сортировка… в диалоговом окне Сортировка диапазона укажите Сортировать по «Столбец C» – по возрастанию. Нажмите кнопку OK. Столбец D заполните через пункт меню Правка/Заполнить/Прогрессия… значениями от 1 до 23. В ячейке B24 запишите формулу =СЧЕТ(B1:B23). В ячейке B24 появится значение 23. В ячейку E1 запишите логическую функцию =ЕСЛИ(A1="Б";D1/($B$24+1);0). Скопируйте ее во все ячейки диапазона E1:E23. Для скважины Б в столбце E получите аргумента i/(n+1). В ячейку G15 введите формулу =1–E15. Скопируйте ее в ячейки G17:G20, G22:G23. Это вспомогательные значения для определения значений функции ψ(i/(n+1)) для положительных Z. По приложению I для скважины Б найдите значения функции ψ(i/(n+1)) при этих значениях аргумента i/(n+1) (см. также примечание к приложению I). Введите их в столбец F. В ячейке F24 подсчитайте сумму записанных значений функции ψ(i/(n+1)) – число 4,19.

Может быть предложен другой порядок расчета. В ячейку F3 ввести формулу =НОРМСТОБР(E3). Эту формулу следует скопировать в ячейки F6, F8, F15, F17–F20, F22–F23 для определения значений функции ψ(i/(n+1)).

Допустимое значение X-критерия Ван-дер-Вардена для уровня значимости 0,1, числа наблюдений 23 и разности между объемами сравниваемых выборок 3, равно 3,12 (см. приложение VII).

Таким образом, гипотеза о равенстве средних значений содержания золота по скважинам и шурфам отвергается. До выяснения причин систематического занижения содержания золота по скважинам использовать их для разведки данного месторождения не рекомендуется.

Непараметрический критерий Вилкоксона (W) также основан на процедуре ранжирования и представляет собой сумму рангов R_i членов меньшей выборки в общем ранжированном ряду из обеих выборок:

.

Если гипотеза о равенстве средних по совокупностям А и Б верна, то есть , математическое ожидание статистики Вилкоксона (MW) и величины возможных отклонений от нее выборочных оценок (W) зависят только от объемов выборок п₁ и п₂.

Для случаев, когда п₁ и п₂ < 25 значения удвоенного математического ожидания критерия Вилкоксона (2МW) и его нижнего критического значения W₁ для заданного уровня значимости α приведены в специальных таблицах (см. приложение VIII). Верхнее критическое значение критерия W₂ определяется из уравнения W₂ = 2MW – W₁. Уровень значимости для W₁ в этих таблицах дан для альтернативы . Поэтому при альтернативе или уровень значимости для нахождения W₁ необходимо уменьшить в два раза.

Если n₁ или n₂ >25, критические значения критерия Вилкоксона можно определить по следующим приближенным формулам:

где – значения функции нормального распределения с параметрами 0,1.

При наличии в объединенной выборке совпадающих значений им дается одинаковый средний ранг, равный среднему арифметическому из всех рангов, приходящихся на данную группу повторяющихся значений, а формула принимает следующий вид:

,

где k – число групп из повторяющихся значений, принадлежащих разным выборкам; t_i – число совпавших значений в группе с номером i (i = 1, 2, 3, …, k).

Группы повторяющихся значений, состоящие полностью из значений выборки А или Б, можно не учитывать при введении поправки.

ЗАДАЧА III.7

Требуется

Выполняя расчеты в электронных таблицах Excel, для приведенного выше ПРИМЕРА III.5 (см. табл. III.10), используя непараметрический критерий Вилкоксона, проверить гипотезу о равенстве средних содержаний золота по шурфам и скважинам.

Указание

Результаты расчетов должны выглядеть так, как это показано на рис. III.17.

Рассчитанное значение критерия Вилкоксона равно 151. По приложению VIII для уровня значимости α/2=0,05 и n₁ = 10, n₂ = 13 с находим: W₁ = 92, 2MW = 240, W₂ = 148. Таким образом, эмпирическое значение критерия Вилкоксона превышает его верхнее критическое значение, следовательно, с вероятностью 0,9 гипотеза о равенстве средних содержаний золота по шурфам и скважинам отвергается.

Рис. III.17. Проверка гипотезы о равенстве средних значений с использованием критерия Вилкоксона

ПРИМЕР III.6

Требуется

Выполняя расчеты в программе STATIATICA, для приведенного выше ПРИМЕРА III.5 (см. табл. III.10), используя непараметрический критерий Вилкоксона, проверить гипотезу о равенстве средних содержаний золота по шурфам и скважинам.

Решение

В системе STATISTICA создается файл данных, используя числовую таблицу III.10. Через меню Data/Cases/Add… вызвать диалоговое окно Add Cases и добавить 3 строки к существующим по умолчанию десяти. Через меню Data/Vars/Delete… удалить столбцы, начиная с третьего по десятый. Далее привести документ к виду, показанному на рис. III.18, заполнив столбцы данными табл. III.10. Сохранить файл.

Рис. III.18. Заполнение столбца Var1 исходными данными

В меню Statistics программы STATISTICA выбирается пункт Nonparametrics и далее раздел Comparing two dependent samples (variables) – расчет для проверки нулевой гипотезы Н₀ об однородности двух генеральных совокупностей по попарно связанным выборкам (рис. III.19). Нажмите OK.

Рис. III.19. Выбор раздела Comparing two dependent samples (variables)

В открывшемся диалоговом окне Comparing two variables нажимается кнопка Variables (переменная). Укажите переменные Var1 и Var2 так как это показано на рис. III.20. Нажмите OK.

Рис. III.20. Ввод имен переменных для исследования

В открывшемся опять диалоговом окне Comparing two variables в поле p-level for highlighting (уровень значимости для указания) по умолчанию установлено значение уровня значимости α/2=0,05. Кнопка Sign test позволяет производить вычисление критерия знаков. Кнопка Box & whisker plot for all variables позволяет строить график «ящик с усами». Здесь следует нажать кнопка Wilcoxon matched pairs test (согласованный парный тест по критерию Вилкоксона) – рис. III.21.

Рис. III.21. Диалоговое окно Comparing two variables

Результирующая таблица приведена на рис. III.22. Объем (Valid) – 10. Значение T-статистики – 15,0; значение Z-статистики – приблизительно 1,274; p-level=P(|Z|>1,274) – приблизительно 0,203. В верхней части таблицы указано Marked test are significant at p < ,05000 – это означает, что отмеченное испытание существенно в пределах уровня значимости.

Рис. III.22. Таблица результатов расчета критерия Вилкоксона

T-статистика – число, равное наименьшему значению суммы рангов отрицательных и положительных разностей. Z-статистика при n > 25 рассчитывается как

.

При условии, что гипотеза гипотезы Н₀ верна, Z имеет (приближенно) стандартное нормальное распределение N(0,1). Гипотеза Н₀ отклоняется на уровне значимости α (при двухсторонней альтернативе), если , где z_в – выборочное значение статистики Z, – квантиль стандартного нормального распределения N(0,1) порядка .

При сравнении двух случайных угловых величин обычно проверяется гипотеза о равенстве круговых средних направлений μ. В случае соответствия обеих выборочных распределений закону Мизеса гипотезу при альтернативе можно проверить с помощью параметрического критерия Ватсона-Вилъямса. Для этого по приведенным выше (см. ЛАБОРАТОРНУЮ РАБОТУ № II. ЗАДАЧА II.1) формулам (II.1, II.2) по выборкам рассчитываются суммарные величины R₁ и R₂, результирующие длины и выборочные круговые средние направления т₁ и т₂ а также общая векторная величина

. (III.6)

С помощью этих параметров вычисляется средняя общая результирующая длина

R=R/(n₁+n₂) (III.7)

и статистика Ватсона-Вильямса

R'= (R₁+ R₂)/(n₁+ n₂). (III.8)

По значению с помощью таблиц функции (см. приложение V) определяется общая оценка параметра концентрации . Предполагается, что параметры концентрации k₁ и k₂ сравниваемых угловых величин равны.

Если 0< <0,7, а n₁ отличается от n₂ не более чем в два раза, критическое значение статистики Ватсона-Вильямса для уровня значимости α = 0,05 можно определить с помощью номограмм, приведенных в приложении IX. Если , гипотеза о равенстве средних круговых направлений отвергается.

При >0,7 для проверки данной гипотезы можно использовать критерий Фишера. В случае 0,7 < < 0,98 эмпирическое значение F-критерия рассчитывается по формуле

а если > 0,98, по более простой формуле

.

Гипотеза H₀ отвергается, если рассчитанное значение F превышает табличное значение критерия Фишера для заданного уровня значимости α при степенях свободы f₁ = l и f₂ = n₁ + n₂ – 2.

ЗАДАЧА III.8

Требуется

Выполняя расчеты в электронных таблицах Excel, проверить в случае соответствия обеих выборочных распределений закону Мизеса гипотезу о равенстве круговых средних направлений μ. На рудопроявлении золота были замерены азимуты падения кварцевых прожилков (см. табл. III.4) и неминерализованных трещин. Для обеих выборок гипотеза о соответствии распределений закону Мизеса не отвергается. Параметры распределения азимутов падения кварцевых прожилков R₁ = 15,16, = 0,316, m₁ = 173,5º, n₁ = 48, = 0,7 (см. ЛАБОРАТОРНУЮ РАБОТУ № III. ЗАДАЧА III.3) и неминерализованных трещин R₂ =16,41, = 0,328, m₂ =166º, n₂ =50, = 0,7.

Указание

По формулам (III.6 – III.8) рассчитаем параметры , , и :

;

; ;

По таблицам приложения V определяем:

.

Так как <0,4, a для нахождения критического значения критерия Ватсона-Вильямса воспользуемся номограммой (см. приложение IX). Для равного 0,32 , следовательно, гипотеза о равенстве круговых средних направлении азимутов падения кварцевых прожилков и неминерализованных трещин не отвергается с доверительной вероятностью 0,95.

Непараметрическим аналогом критерия Ватсона-Вильямса является ранговый критерий равномерных меток Вилера-Ватсона-Ходжеса, применение которого не ограничивается условием соответствия выборочных данных какому-либо определенному закону распределения.

Построение этого критерия основано на объединении двух сравниваемых выборок объемом n₁ (меньшая выборка) и n₂ в общую выборку объемом n= n₁ + n₂ и ранжировании всех замеров в порядке возрастания угловых величин. Фактические замеры заменяются величинами , где R_i – ранг, то есть порядковый номер замера в общем ранжированном ряду. Эта операция соответствует размещению замеров по двум выборкам на окружности 2π в порядке их возрастания на одном расстоянии друг от друга, равном 2π/n. Ранговый критерий равномерных меток представляет собой величину , где

,

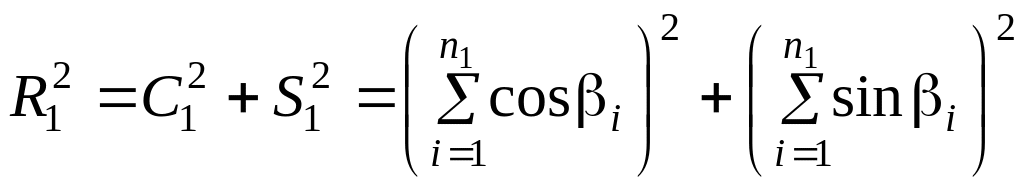то есть квадрат длины результирующего вектора для точек на окружности, соответствующих значениям меньшей по объему выборки.

Для малых выборок (n≤20) рассчитаны таблицы критических значений статистики R*. При n>20, если гипотеза Н₀ о равенстве круговых средних верна, статистика R* распределена приближенно как χ² с двумя степенями свободы. Поэтому ее критические значения для заданного уровня значимости можно найти с помощью приложения III.

ПРИМЕР III.7

Требуется

Выполняя расчеты в электронных таблицах Excel, проверить гипотезу о равенстве круговых средних азимутов простирания линейных складок и разрывных нарушений.

В пределах рудного поля оси линейных складок и основные рудоконтролирующие разрывные нарушения ориентированы в северо-восточном направлении (см. табл. III.12).

Решение

Для определения рангов общей выборки (см. табл. III.12) используются замеры по обеим выборкам, а расчет значений β_i, и статистик производится только по замерам азимутов разрывных нарушений, составляющим выборку меньшего объема.

Таблица III.12. Азимуты простирания разрывных нарушений и осей складок

№ п/п	Складки, азимут	№ п/п	Разрывные нарушения, азимут
1	42	1	23
2	40	2	26
3	20	3	16
4	24	4	62
5	28	5	38
6	14	6	18
7	32	7	12
8	42	8	30
9	56	9	10
10	22	10	12
11	40	11	30
12	20
13	40
14	32
15	19
16	46

В столбец B введите значения порядковых номеров складок: от 1 до 16 (ячейки B1:B16), в столбец C – азимуты линейных складок (ячейки C1:C16) – см. табл. III.12, затем значения порядковых номеров разрывных нарушений: от 1 до 11 (ячейки B17:B27), в столбец C – азимуты разрывных нарушений (ячейки C17:C27) – см. табл. III.12. В ячейки A1:A16 введите символ А, в ячейки A17:A27 – символ Б. Выделите диапазон A1:C27 и через пункт меню Данные/Сортировка… в диалоговом окне Сортировка диапазона укажите Сортировать по «Столбец C» – по возрастанию. Нажмите кнопку OK.

Столбец D заполните через пункт меню Правка/Заполнить/Прогрессия… значениями от 1 до 27. В ячейке A28 запишите n. В ячейке B28 запишите формулу =СЧЕТ(B1:B27). В ячейке B28 появится значение 27. В ячейку E1 запишите логическую функцию =ЕСЛИ(A1="Б";C1;""). Скопируйте ее во все ячейки диапазона E1:E27. В ячейку F1 запишите логическую функцию =ЕСЛИ(A1="Б";360*D1/$B$28;""). Скопируйте ее во все ячейки диапазона F1:F27. В ячейку G1 запишите логическую функцию =ЕСЛИ(A1="Б";SIN(РАДИАНЫ(F1));""). Скопируйте ее во все ячейки диапазона G1:G27. В ячейку H1 запишите логическую функцию =ЕСЛИ(A1="Б";COS(РАДИАНЫ(F1));""). Скопируйте ее во все ячейки диапазона H1:H27. В ячейку G28 запишите формулу =СУММ(G1:G27), а в ячейку H28 запишите формулу =СУММ(H1:H27). В ячейке A29 запишите n1, а в ячейке A30 запишите n2. В ячейку B29 запишите формулу =СЧЁТЕСЛИ(A1:A27;"А"), а в ячейку B30 запишите формулу =СЧЁТЕСЛИ(A1:A27;"Б"). Запишите текст в ячейках: A31 – R^2, A32 – R*, A33 – хи^2, запишите формулы в ячейках: B31 – =G28^2+H28^2, B32 – =2*(B28-1)*B31/(B29*B30), B33 – =ХИ2ОБР(0,1;2).

Значение критерия χ² для уровня значимости α =0,1 и числа степеней свободы f = 2 равно 4,605 и значительно превышает рассчитанную величину статистики. Значение критерия χ² для уровня значимости α =0,1 и числа степеней свободы f = 2 можно определить и с помощью приложения III. При уменьшении уровня значимости величина χ² возрастает, поэтому отвергать гипотезу о равенстве круговых средних направлений осей складок и азимутов простирания разрывных нарушений нет оснований.

ПРОВЕРКА ГИПОТЕЗ О РАВЕНСТВЕ ДИСПЕРСИЙ

Сравнение геологических объектов по степени изменчивости, которая оценивается по величине дисперсии или коэффициента вариации тех или иных свойств, необходимо для обоснованного применения принципа аналогии при их изучении. Так, например, дисперсия мощности рудных тел характеризует сложность их строения.

Различие в дисперсиях свойств аналогичных по составу геологических объектов может указывать и на различие в истории их формирования. Так различие дисперсий содержаний основных породообразующих минералов в двух схожих по составу комплексах магматических пород может указывать на то, что комплекс, для которого характерна большая степень рассеяния содержаний, формировался в течение более длительного периода и в нем сильнее проявились процессы дифференциации.

Различные горные породы, сходные по средним значениям физических свойств – магнитной восприимчивости, электропроводимости и т.п., часто отличаются по степени изменчивости этих свойств. Поэтому путем проверки гипотез о равенстве (различии) дисперсий можно проводить литологическое расчленение разрезов по данным геофизического каротажа скважин при бескерновом бурении, а также интерпретировать результаты геофизических съемок при составлении геологических карт.

На сравнении дисперсий основаны также методы определения величин случайных погрешностей различных способов опробования и анализов. Если количественные данные о свойствах геологического объекта получены различными способами, то более надежным следует признать тот способ, который дает меньший разброс значений изучаемого свойства, то есть характеризуется меньшей дисперсией.

Критерий Фишера. Критерий Фишера используют для проверки гипотезы о принадлежности двух дисперсий одной генеральной совокупности и, следовательно, их равенстве. При этом предполагается, что данные независимы и распределены по нормальному закону. Гипотеза о равенстве дисперсий принимается, если отношение большей дисперсии к меньшей меньше критического значения распределения Фишера

,

где зависит от уровня значимости и числа степеней свободы для дисперсий в числителе и знаменателе.

Для проверки гипотезы о равенстве дисперсий и обычно используется критерий Фишера F. Р. Фишером было установлено, что в случае равенства дисперсий двух нормально распределенных случайных величин, величина при распределена по закону Фишера с п₁ – 1 и п₂ – 1 степенями свободы, где п₁ – количество членов в выборке, по которой получена большая оценка дисперсии , а п₂ – объем второй выборки. Процедура проверки гипотезы сводится к нахождению эмпирического значения F-критерия и сравнению его с табличным значением для принятой доверительной вероятности (1 – α) и степенях свободы f₁ = п₁ – 1 и f₂ = п₂ – 1. Если вычисленное значение критерия Фишера превышает табличное, то гипотеза о равенстве двух дисперсий отвергается.

В приложении X приведены критические значения F-критерия для уровня значимости α и альтернативной гипотезы . При сложной альтернативе , то есть или , критическое значение критерия Фишера находят для уровня значимости α/2.

В условиях асимметричных распределений критерий Фишера обладает малой мощностью. В случае логнормального распределения сравниваемых совокупностей при использовании этого критерия необходимо пользоваться максимально правдоподобными оценками дисперсий или проверять гипотезу о равенстве дисперсий логарифмов значений исследуемого признака.

В Excel для расчета уровня вероятности выполнения гипотезы о равенстве дисперсий могут быть использованы функция ФТЕСТ(массив 1;массив2) и процедура пакета анализа Двухвыборочный F-тест для дисперсий.

Функция ФТЕСТ(массив1; массив2) возвращает результат F-теста.

• Массив1 – это первый массив или интервал данных.

• Массив2 – это второй массив или интервал данных. F-тест возвращает одностороннюю вероятность того, что дисперсии аргументов массив1 и массив2 различаются несущественно. Эта функция используется для того, чтобы определить, имеют ли две выборки различные дисперсии.

ЗАДАЧА III.9

Воспользоваться статистическими характеристиками, приведенными в табл. III.9, и проверить гипотезу о равенстве дисперсий содержаний Na₂O, К₂О и TiО₂ в гранитах неизвестного возраста и гранитах средне- и верхнепалеозойского комплексов при альтернативе и уровне значимости α/2=0,05.

Требуется

В электронных таблицах Excel произвести сравнение гранитов неизвестного возраста со среднепалеозойскими гранитами и верхнепалеозойскими гранитами.

Указание

Сравнение гранитов неизвестного возраста со среднепалеозойскими гранитами:

по Na₂O ;

по К₂О ;

по TiО₂ .

Сравнение гранитов неизвестного возраста с верхнепалеозойскими гранитами:

по Na2O ;

по К2О ;

по TiО2 .

Критические значения критерия Фишера могут быть вычислены в программе Excel с помощью функция FРАСПОБР для заданных вероятности и степеней свободы.

Во всех случаях рассчитанные значения критерия Фишера оказались меньше критических, следовательно, рассматриваемые граниты существенно не отличаются по степени изменчивости содержаний данных химических элементов как от среднепалеозойских, так и от верхнепалеозойских гранитов. Поэтому характеристики изменчивости в данном случае нельзя использовать и качестве классификационного признака.

Непараметрическим аналогом критерия Фишера является критерий Сиджела-Тьюки, по процедуре вычисления во многом сходный с критерием Вилкоксона. Он применим для распределений любого вида и не чувствителен к аномальным значениям, поэтому весьма удобен для решения геологических задач, особенно по выборкам милого объема.

Критерий Сиджела-Тьюки построен исходя из предположения о равенстве центров распределения сравниваемых совокупностей. Поэтому в случае несоблюдения этого условия исходные данные по каждой выборке необходимо центрировать относительно их медиан, то есть сравнивать не сами значения изучаемых параметров, а их отклонения от медиан.

Значения сравниваемых выборочных совокупностей объединяются в общую выборку и записываются в виде вариационного ряда в порядке их возрастания: х₁< х₂< х₃<...< х_N-1, где N= п₁ + п₂ – объем общей выборки; п₁ –объем меньшей выборки. Члены вариационного ряда, в свою очередь, ранжируются следующим образом: ранг 1 приписывается наименьшему члену ряда х₁, ранг 2 – наибольшему, то есть х_N; ранг 3 – значению х₂; ранг 4 –значению х_N-1 и т.д. Если N нечетно, то медианному значению ранг не присваивается. При таком ранжировании значениям выборки с меньшей дисперсией будут присваиваться преимущественно большие ранги, а значениям выборки с большей дисперсией – наоборот, малые. В случае равенства дисперсий значения из разных выборок будут чередоваться в ранжированном ряду случайно, и сумма рангов, относящихся к членам меньшей по объему выборки, будет обладать всеми свойствами рассмотренного выше критерия Вилкоксона (W). Дальнейшая проверка гипотезы о равенстве дисперсий сводится к нахождению критических значений W₁ и W₂ по описанной выше процедуре и сравнению с ними рассчитанного значения W.

ЗАДАЧА III.10

По одному из участков молибден-вольфрамового месторождения для контроля бороздовых проб (выборка А) отобрано 16 валовых проб большой массы (выборка Б).

Требуется

Выполняя расчеты в электронных таблицах Excel, проверить гипотезу о равенстве средних значений и дисперсий содержаний молибдена по пробам, отобранным разным способом, при альтернативах , и уровне значимости α = 0,1.

Указание

Результаты расчетов должны выглядеть так, как это показано на рис. III.23.

Рис. III.23. Проверка гипотезы о равенстве средних значений и дисперсий с использованием критериев Вилкоксона и Сиджела-Тьюки

Записать приведенные в табл. III.13 результаты опробования в виде ранжированного ряда (табл. III.14, графа 2) и определить ранги R₁ для расчета критерия Вилкоксона W (см. табл. III.14, графа 4). Найти критические значения критерия Вилкоксона для n₁ =16, n₂ =20 и α/2==0,05: W₁=234; 2MW = 592 (см. приложение VIII); W₂ = 2MW – W₁ = 358. Расчетное значение критерия W, определенное по сумме рангов значений из меньшей выборки Б, равно 250, то есть находится в интервале между нижним и верхним критическими значениями критерия Вилкоксона. Следовательно, гипотеза о равенстве средних содержаний молибдена по пробам разной массы не отвергается.

Ввиду равенства средних значений при проверке гипотезы о равенстве дисперсий нет необходимости в центрировании данных. Выполнив ранжирование по способу Сиджела-Тьюки (см. табл. III.14, графа 5), получить значение критерия W для проверки гипотезы о равенстве дисперсий. Оно равно 354 и не превышает верхнее критическое значение критерия W₂. Следовательно, гипотеза о равенстве дисперсий не отвергается. Дисперсия содержаний молибдена по бороздовым пробам существенно выше, чем по валовым.

Таблица III.13. Содержание (в %) молибдена но бороздовым (выборкам А) и валовым пробам (выборка Б)

Выборка А				Выборка Б
№ п/п	Содержание Mo	№ п/п	Содержание Мо	№ п/п	Содержание Мо	№ п/п	Содержание Мо
1	0,065	11	0,082	1	0,056	11	0,046
2	0,075	12	0,061	2	0,078	12	0,056
3	0,110	13	0,022	3	0,067	13	0,088
4	0,140	14	0,070	4	0,120	14	0,104
5	0,182	15	0,140	5	0,038	15	0,054
6	0,010	16	0,060	6	0,062	16	0,064
7	0,192	17	0,025	7	0,072
8	0,310	18	0,230	8	0,167
9	0,037	19	0,180	9	0,068
10	0,160	20	0,105	10	0,059

Таблица III.14. Проверка гипотезы о равенстве средних и дисперсий содержаний (в %) молибдена по бороздовым и валовым пробам

№ п/п	Содержание Мо	Выборка	Ранг по критерию Вилкоксона (R1)	Ранг по критерию Сиджела-Тьюки (R2)
1	0,010	А	1	1
2	0,022	А	2	3
3	0,025	А	3	5
4	0,037	А	4	7
5	0,038	Б	5	9
6	0,046	Б	6	11
7	0,054	Б	7	13
8	0,056	Б	8,5	15
9	0,056	Б	8,5	17
10	0,059	Б	10	19
11	0,060	А	11	21
12	0,061	А	12	23
13	0,062	Б	13	25
14	0,064	Б	14	27
15	0,065	А	15	29
16	0,067	Б	16	31
17	0,068	Б	17	33
18	0,070	А	18	35
19	0,072	Б	19	36
20	0,075	А	20	34
21	0,078	Б	21	32
22	0,082	А	22	30
23	0,088	Б	23	28
24	0,104	Б	24	26
25	0,105	А	25	24
26	0,110	А	26	22
27	0,120	Б	27	20
28	0,140	А	28,5	18
29	0,140	А	28,5	16
30	0,160	А	30	14
31	0,167	Б	31	12
32	0,180	А	32	10
33	0,182	А	33	8
34	0,192	А	34	6
35	0,230	А	35	4
36	0,310	А	36	2

n₁ = 16; n₂ = 20; α/2 = 0,05;

W = Σ R₁ (по выборке Б) = 250; W' = Σ R₂ (по выборке Б) = 354; W₁ = 234 (см. табл. III.13); 2M W = 592 (см. табл. III.13); W₂ = 2M W – W₁ = 358.

Результаты проверки гипотез позволяют сделать следующие выводы:

• различие в средних содержаниях молибдена по пробам разной массы несущественно, следовательно опробование малыми пробами не приведет к систематическим ошибкам в оценке среднего качества руд;

• содержания по бороздовым пробам отличаются большим разбросом, следовательно для оценки среднего содержания молибдена с заданной точностью их требуется значительно больше, чем валовых.

Разделение полимодальных распределений можно выполнять также путем анализа геологических неоднородностей изучаемого объекта.

АНАЛИЗ ОДНОРОДНОСТИ ВЫБОРОЧНЫХ ГЕОЛОГИЧЕСКИХ СОВОКУПНОСТЕЙ

При использовании одномерных статистических моделей для описания свойств геологических объектов предполагается, что данный объект однороден в отношении изучаемого свойства. Обычно вопрос об однородности решается исходя из принятой геологической модели. Исследуемый объект считается статистически однородным, если он однороден по геологическому строению. Однако на ранних стадиях изучения трудно однозначно решить вопрос о геологической однородности на основе только качественной геологической информации. В этих случаях можно использовать обратный прием – получать суждение о геологической однородности объекта путем проверки гипотезы о его статистической однородности, используя количественные данные о характере изменчивости его свойств.

Задачи, основанные на проверке гипотезы о статистической однородности геологических объектов, можно разделить на три типа:

• выделение аномальных значений;

• разделение неоднородных выборочных совокупностей;

• оценка степени влияния различных факторов на характер изменчивости свойств геологических объектов.

Выявление локальных неоднородностей (аномалий) в строении геологических объектов имеет исключительно важное практическое значение при проведении поисковых работ, так как они часто используются в качестве признаков, указывающих на наличие повышенных концентраций полезных ископаемых.

Наличие же в выборочных совокупностях резко выдающихся значений, обусловленных локальными причинами и не характерных для данного геологического объекта, в целом, снижает точность вычисления точечных и интервальных оценок средних параметров и затрудняет решение рассмотренных выше задач на основе проверки гипотез о равенстве средних и дисперсий.

Для выделения аномальных значений совокупность результатов наблюдений рассматривается как выборка из двух различных генеральных совокупностей – «фоновой» и «аномальной». При этом аномальные значения присутствуют в выборке в очень небольшом количестве или совсем отсутствуют.

В случаях нормального распределения фоновой генеральной совокупности эта задача решается с помощью параметрических критериев Смирнова и Фергюссона.

Н.В. Смирновым было установлено, что если максимальный по значению член выборочной совокупности не является аномальным, то величина имеет распределение, названное его именем. В данной формуле – максимальный член выборки; – среднее арифметическое; – смещенная оценка дисперсии, которая рассчитывается через несмещенную оценку дисперсии S² по формуле .

Если рассчитанное значение критерия больше допустимого, определенного по таблицам распределения Смирнова для заданной доверительной вероятности и п степеней свободы, то максимальное значение выборки следует считать аномальным.

Критерий Фергюссона основан на том, что если выборочная совокупность не содержит аномальных значений, то оценка коэффициента асимметрии А будет распределена асимптотически нормально с математическим ожиданием 0 и дисперсией .

Если рассчитанное значение коэффициента асимметрии превышает табличное для заданной доверительной вероятности и п степеней свободы, то максимальное значение выборки следует признать аномальным. Если распределение фоновой совокупности отличается от нормального, то «аномальными» будут признаваться все редко встречающиеся большие значения, принадлежащие исследуемой генеральной совокупности. Это ограничивает область применения обоих критериев. Они могут применяться только в том случае, если заранее известно, что распределение фоновой совокупности является нормальным.

В практике геохимических исследований за аномальные значения часто принимают маловероятные значения, по абсолютной величине превышающие или (то есть отличающиеся от среднего на утроенное или удвоенное значение стандартного отклонения). Однако этот способ нельзя признать корректным, так как он не гарантирует от ошибок как первого, так и второго рода, причем вероятность этих ошибок оценить нельзя.

ЛАБОРАТОРНАЯ РАБОТА № IV. ОДНОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. ОДНОФАКТОРНЫЙ И ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ В ГЕОЛОГИИ

Свойства геологических объектов, как и любой другой сложной природной системы, обычно зависят от ряда факторов, обусловливающих их изменчивость. Выявление этих факторов и оценка степени их влияния на изменчивость (неоднородность) свойств изучаемых объектов осуществляется с помощью дисперсионного анализа.

Математический аппарат дисперсионного анализа описан в специальных пособиях по теории вероятностей и математической статистике. Дисперсионный анализ предназначен для исследования задачи о действии на измеряемую случайную величину (отклик) одного или нескольких независимых факторов, имеющих несколько градаций. Причем в однофакторном, двухфакторном и т.д. анализе влияющие на результат факторы считаются известными, и речь идет только о выяснении существенности или оценке этого влияния.

Применение дисперсионного анализа возможно, если можно предполагать соответствие выборочных групп генеральным совокупностям с нормальным распределением и независимость распределений наблюдений в группах.

С помощью дисперсионного анализа решается широкий круг геологических задач:

• проверяются гипотезы о влиянии литологических, петрофизических, геохимических, структурных и других факторов на локализацию оруденения;

• выявляются элементы зональности различных геологических объектов;

• определяется влияние способа отбора проб на их достоверность и представительность;

• оценивается влияние ландшафтных условий на интенсивность проявления различных поисковых признаков;

• решается вопрос о влиянии гипергенных процессов на качество руд;

• выявляются фактора, определяющие прочностные свойства грунтов и пород и т.д.

При равномерном однофакторном дисперсионном анализе случайной величины х относительно фактора А, имеющего p уровней при количестве замеров на каждом уровне равном q, результаты наблюдений обозначаются как x_ij, где i – номер наблюдения (i= 1, 2, ..., q), a j – номер уровня фактора (j = 1, 2, ..., p) и записываются в виде табл. IV.1.

Таблица IV.1. Однофакторный дисперсионный анализ

Номер изменения	Уровень фактора
	A1	A2	…	Ap
1	x11	x12	…	x1p
2	x21	x22	…	x2p
…	…	…	…	…
q	xq1	xq2	…	xqp
Групповые средние			…

По этим данным рассчитываются следующие статистики:

1) общая сумма квадратов отклонений наблюдаемых значений признака от общей средней :

;

2) факторная сумма квадратов отклонений групповых средних от общей средней, характеризующая рассеяние между группами:

;

3) остаточная сумма квадратов отклонений наблюдаемых значений от своей групповой средней, характеризующая рассеяние внутри групп:

.

Вычислительные операции при однофакторном дисперсионном анализе можно упростить, используя равенство С_ост = С_общ – С_факт;

4) общая, факторная и остаточная дисперсии:

; ; ;

5) значение критерия Фишера:

.

Значение критерия Фишера сравнивается с критическим для заданного уровня значимости α и числа степеней свободы k₁ = p – 1 и k₁ = p(q – 1).

При неравномерном однофакторном дисперсионном анализе, когда количество наблюдений на уровне А₁ равно q₁ на уровне А₂ – q₂, на уровне А_k – q_p. В этом случае общую сумму квадратов отклонений находят по формуле

(IV.1),

где – сумма квадратов наблюдавшихся значений признака на уровне A₁;

– сумма квадратов наблюдавшихся значений признака на уровне A₂;

………………………………………………………………………………….

– сумма квадратов наблюдавшихся значений признака на уровне A_p;

, , …, – суммы наблюдавшихся значений признака соответственно на уровнях A₁, A₂, …, A_p;

– общее число испытаний (объем выборки).

Факторную сумму квадратов отклонений находят по формуле

(IV.2).

Остаточную сумму квадратов отклонений находят по формуле

С_ост = С_общ – С_факт (IV.3).

Остальные операции выполняются так же, как и в случае одинакового числа испытаний:

; ; (IV.4).

Значение критерия Фишера сравнивается с критическим для заданного уровня значимости α и числа степеней свободы k₁ = p – 1 и k₂ = n – p.

ЗАДАЧА IV.1

При изучении гидротермального свинцово-цинкового месторождения в гранитах высказано предположение, что на интенсивность процесса рудоотложения влияла степень предрудного метасоматического изменения пород. Для проверки этой гипотезы результаты опробования на свинец по 43 разведочным пересечениям были разделены на три группы: в слабо измененных (уровень A₁), в средне измененных (уровень A₂) и сильно измененных (уровень A₃) гранитах (см. табл. IV.2).

Таблица IV.2. Проверка гипотезы о влиянии предрудного метасоматического изменения гранитов на содержание свинца в руде

№ заме-ра i	Уровни факторов А
	A1		A2		A3
	xi1		xi2		xi3
1	1,17		2,28		1,80
2	1,52		2,46		2,38
3	1,90		0,88		2,62
4	1,76		2,03		2,91
5	1,54		1,22		1,60
6	0,63		2,29		2,83
7	2,30		1,80		2,13
8	1,32		1,79		2,06
9	0,94		1,61		2,23
10	1,15		2,30		3,06
11	0,75		2,60		1,86
12	2,49		1,76		1,92
13	2,14		2,14		2,16
14	1,62		2,73		2,27
15	1,40
Σ	22,63		27,89		31,83

Требуется

Выполнить в электронных таблицах Excel расчеты по схеме однофакторного дисперсионного анализа для случая неодинакового числа испытаний для каждого уровня фактора.

Указание

При неравномерном однофакторном дисперсионном анализе расчет следует выполнять по формулам (IV.1 – IV.4).

Окончательный результат расчета будет выглядеть, как показано на рис. IV.1.

Критическое значение критерия Фишера F в ячейке F29 следует вычислить по формуле =FРАСПОБР(F26;C26;C25). Его можно найти также по таблице приложения X.

Рис. IV.1. Окончательный вид результата расчета по схеме однофакторного дисперсионного анализа

Таким образом, с достаточно высокой доверительной вероятностью гипотеза об отсутствии влияния степени метасоматического изменения гранитов на содержание свинца в руде отвергается, и предрудный метасоматоз должен рассматриваться как один из ведущих рудоконтролирующих факторов.

В Excel для проведения однофакторного дисперсионного анализа может быть использована процедура Однофакторный дисперсионный анализ.

Для проведения дисперсионного анализа необходимо:

• ввести данные в таблицу, так чтобы в каждом столбце оказались данные, соответствующие одному значению исследуемого фактора, а столбцы располагались в порядке возрастания (убывания) величины исследуемого фактора;

• выполнить команду Сервис/Анализ данных;

• в появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать процедуру Однофакторный дисперсионный анализ, указав курсором мыши и щелкнув левой кнопкой мыши. Затем нажать кнопку OK;

• в появившемся диалоговом окне задать Входной интервал, то есть ввести ссылку на диапазон анализируемых данных, содержащий все столбцы данных. Для этого следует навести указатель мыши на верхнюю левую ячейку диапазона данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней правой ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

• в разделе Группировка переключатель установить в положение по столбцам;

• указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные.

• нажать кнопку OK.

Результаты анализа. Выходной диапазон будет включать в себя результаты дисперсионного анализа: средние, дисперсии, критерий Фишера и другие показатели.

Интерпретация результатов. Влияние исследуемого фактора определяется по величине значимости критерия Фишера, которая находится в таблице Дисперсионный анализ на пересечении строки Между группами и столбца P-Значение. В случаях, когда P-Значение < 0,05, критерий Фишера значим и влияние исследуемого фактора степень предрудного метасоматического изменения пород можно считать доказанным.

ПРИМЕР IV.1

Требуется

Необходимо выполнить ЗАДАЧУ IV.1 с использованием пакета анализа.

Решение

1. Исследуемые данные введите в рабочую таблицу Excel по столбцам: в столбец А – фактор А₁, в столбец В – фактор А₂, в столбец C – фактор А₃ (диапазон А1:С16).

2. Выполните команду Сервис/Анализ данных. В появившемся диалоговом окне Анализ данных в списке Инструменты анализа щелчком мыши выберите процедуру Однофакторный дисперсионный анализ. Нажмите кнопку OK.

3. В появившемся диалоговом окне Однофакторный дисперсионный анализ в поле Входной интервал задайте A1:С16. Для этого наведите указатель мыши на ячейку А1 и протяните его к ячейке С16 при нажатой левой кнопке мыши.

4. В разделе Группировка переключатель установите в положение по столбцам.

5. Далее необходимо указать выходной диапазон. Для этого поставьте переключатель в положение Выходной интервал (наведите указатель мыши и щелкните левой кнопкой), затем щелкните указателем мыши в правом поле ввода Выходной интервал, и щелчком мыши на ячейке F2 укажите расположение выходного диапазона. Нажмите кнопку OK.

Результаты анализа. В результате будет получена таблица, содержащая результаты однофакторного дисперсионного анализа.

Интерпретация результатов. В таблице Дисперсионный анализ на пересечении строки Между группами и столбца P-Значение находится величина 0,000826. Величина P-Значение < 0,05, следовательно, критерий Фишера значим, и влияние фактора доказано статистически.

Результаты расчета приведены на рис. IV.2. Найдите соответствие полученных результатов, полученных по формулам (см. ЗАДАЧА IV.1) и в результате использования Пакета анализа (см. ПРИМЕР IV.1).

Рис. IV.2. Окончательный вид результата расчета с помощью процедуры

При двухфакторном дисперсионном анализе сумма квадратов отклонений от общего среднего разделяется на компоненты, отвечающие двум предполагаемым факторам изменчивости – А и В. Если по фактору А выделяется р уровней, а по фактору B – q уровней, то общее количество групп будет равно m=pq, а исходные данные можно записать в виде табл. IV.3.

Если для каждого сочетания факторов A_iB_i произведено по п наблюдений (двухфакторный дисперсионный анализ с повторением), то в каждую клетку табл. IV.3 помещается п значений, а единичное наблюдение обозначается как x_ijk, где k = l, 2, ..., п. Оценки средних значений по группам ( ), по факторам (x_i.. и x_.j.) и общее среднее ( ) в этом случае рассчитываются по формулам

;

;

.

Таблица IV.3. Двухфакторный дисперсионный анализ

А	Уровни фактора В						Среднее
	B1	B1	…	Bj	…	Bq
A1			…		…
A2			…		…
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
Ai
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
Ap			…		…
Среднее			…		…

Общая схема вычисления дисперсий при двухфакторном анализе приведена в табл. IV.4.

Проверка гипотезы о влиянии на изменчивость изучаемого свойства каждого фактора в отдельности и их совместного влияния производится по критерию Фишера:

; ; .

Полученные значения F-критерия сравниваются с критическим для заданного уровня значимости и числа степеней свободы, приведенного в табл. IV.4.

Таблица IV.4. Схема вычисления дисперсий при двухфакторном дисперсионном анализе

Вид дисперсии	Сумма квадратов отклонений	Число степеней свободы	Дисперсия
Факторная по фактору А		p – 1
Факторная по фактору В		q – 1
Смешанная по факторам АВ		(p – 1)(q – 1)
Остаточная		pq(n – 1)
Общая		npq – 1

При расчете F-критерия в данном случае в знаменателе всегда берется остаточная дисперсия. Поэтому его значение иногда может получиться меньше 1.

Кроме рассмотренной процедуры однофакторного дисперсионного анализа, для проведения двухфакторного дисперсионного анализа в пакете анализа программы Excel реализованы процедуры Двухфакторный дисперсионный анализ с повторениями и Двухфакторный дисперсионный анализ без повторений.

Приведенные схемы дисперсионного анализа основаны на свойствах нормального закона распределения и предположении о равенстве дисперсий на разных уровнях одного и того же фактора. Однако F-критерий по выборкам достаточно большого объема устойчив и для совокупностей, умеренно отклоняющихся от нормальных. Умеренное различие в дисперсиях так же не является препятствием для его применения при условии приблизительного равенства объемов выборок по группам. Если возможность применения F-критерия все же вызывает сомнения можно воспользоваться непараметрическими критериями.

Однофакторный непараметрический дисперсионный анализ производится с применением критерия Краскала-Уоллиса. При двухфакторном непараметрическом анализе используется критерий Фридмана.

Однофакторный непараметрический дисперсионный анализ с применением критерия Краскала-Уоллиса включает следующие операции:

• ранжирование всех наблюдений по возрастанию от 1 до N, где – объем всей выборки;

• нахождение сумм рангов R₁, R₂, ..., R_k для каждого уровня анализируемого фактора;

• вычисление критерия Краскала-Уоллиса по формуле

;

• сравнение полученного значения Н с его критическим значением (H_к) для принятого уровня значимости α (см. приложение XI).

При достаточно большом объеме выборки, когда количество наблюдений по каждому уровню превышает 5, значение H_к определяется по таблицам распределения χ² для числа степеней свободы f = k – 1, где k – количество уровней исследуемого фактора.

Для малых выборок критические значения критерия Краскала-Уоллиса определяются по специальным таблицам (приложение XI).

Если рассчитанное значение критерия Н превышает H_к, то гипотеза об отсутствии влияния анализируемого фактора на изменчивость изучаемого свойства отвергается.

ЗАДАЧА IV.2

Требуется

Необходимо выполнить ЗАДАЧУ IV.1, используя непараметрический критерий Краскала-Уоллиса, поскольку возможность применения F-критерия вызывает сомнения. Для решения использовать программу Excel.

Указание

В столбец A поместить данные из табл. IV.2: в диапазон A1:A15 – значения для фактора А₁, в диапазон A16:A29 – значения для фактора А₂, в диапазон A30:A43 – значения для фактора А₃. В столбец B поместить обозначения уровня фактора для каждого значения, в столбец C поместить номер замера соответствующего фактора из табл. IV.2 для каждого значения фактора. Отсортировать столбец A по возрастанию и в столбец D ввести ранги от 1 до 43. Составить в диапазоне G2:I16 таблицу рангов по уровням факторов и номерам замеров, рассчитать суммы R и число замеров для каждого уровня фактора. В ячейке G22 вычислить критерий Краскала-Уоллиса по формуле приведенной выше.

Сравнить расчетный величину критерия Краскала-Уоллиса с критической величиной критерия и сделать вывод.

Критическое значение H_к определено по таблицам распределения χ² (см. приложение III) для числа степеней свободы f_к = 2. Результат расчета будет выглядеть так, как показано на рис. IV.3.

Рис. IV.3. Окончательный вид результата расчета с применением критерия Краскала-Уоллиса

ЗАДАЧА IV.3

Требуется

Необходимо выполнить ЗАДАЧУ IV.1, используя непараметрический критерий Краскала-Уоллиса, поскольку возможность применения F-критерия вызывает сомнения. Для решения использовать программу STATISTICA.

Указание

Все три выборки вводятся в одну переменную, которая переименована из Var 1 в dependent var, каждая выборка обозначена своим кодом (1, 2, 3), коды выборок вводятся в группирующую переменную – grouping var – см. рис. IV.4.

Рис. IV.4. Заполнение столбцов исходными данными

Для выполнения дисперсионного анализа Краскала-Уоллиса следует открыть меню Statistics программы STATISTICA и выбрать пункт Nonparametrics. В диалоговом окне Nonparametrics Statistics следует выбрать раздел Comparing multiple indep. samples (groups). В открывшемся диалоговом окне Kruskal-Wallis ANOVA & Median test следует выбрать переменные для исследования кнопкой Variables (рис. IV.5) и затем кнопкой Summary: Kruskal-Wallis ANOVA & Median test выполнить расчет. Результат выполнения однофакторного дисперсионного анализа Краскала-Уоллиса приведен на рис. IV.6.

Обсудить результаты.

Рис. IV.6. Выбор имен переменных для исследования

Рис. IV.6. Результат однофакторного дисперсионного анализа Краскала-Уоллиса

При двухфакторном непараметрическом анализе Фридмана исходные данные записываются в виде табл. IV.3.

Для проверки влияния фактора А значения в строках таблицы ранжируются, то есть заменяются цифрами от 1 до q. По каждому столбцу вычисляется сумма рангов – R_j(j =1, ..., р), рассчитывается статистика и критериальная статистика .

Для количества уровней по факторам А или В больше 4, критическое значение статистики определяется по таблицам критерия χ² для количества степеней свободы f = q – 1, а при малом количестве уровней используются специальные таблицы (приложение XII).

Для проверки гипотезы о влиянии фактора В строки и столбцы в табл. IV.3 меняются местами.

ЗАДАЧА IV.4

Требуется

Произвести проверку гипотезы о влиянии степени метасоматического изменения вмещающих пород на их петрофизические свойства с помощью двухфакторного дисперсионного анализа.

На редкометалльном месторождении отмечены процессы предрудного метасоматоза, выразившиеся в появлении новообразованного альбита, карбонатов и кварца. Высказано предположение о том, что предрудный метасоматоз привел к изменению петрофизических свойств пород и явился благоприятным фактором для рудоотложения. В табл. IV.5 приведены результаты испытаний штуфных проб, отобранных из пород различного состава. По степени метасомагических изменений породы разделены на три класса: 1) слабо измененные; 2) средне измененные; 3) сильно измененные.

Проверка гипотезы о влиянии степени метасоматической проработки на петрофизические свойства пород затруднена ввиду разнообразия вмещающих пород, различия их исходных петрофизических свойств и малого количества проб по каждой разновидности пород. Решить эту задачу можно с помощью двухфакторного дисперсионного анализа, В качестве первого фактора в данной задаче выступает состав пород, а в качестве второго фактора – степень их метасоматического изменения.

Таблица IV.5 Петрофизические свойства пород

Горные породы	Степень измене-ния	Коли-чество проб	Модуль, 105 кг/см2		Коэффи-циент Пуассона, м	Объемная масса, г/см3	Эффек-тивная пористость, %
			Юнга	сдвига
Аргиллиты	1	4	7,85	3,49	0,130	2,808	0,488
	2	4	–	–	–	2,782	0,735
	3	4	5,70	2,46	0,161	2,771	1,120
Алевролиты	1	5	7,89	3,25	0,240	2,766	0,412
	2	5	7,43	2,88	0,295	2,805	0,542
	3	6	6,51	2,69	0,295	2,808	0,827
Песчаники	1	12	8,18	3,40	0,203	2,719	0,315
	2	5	8,12	3,32	0,220	2,737	0,532
	3	4	7,05	2,82	0,296	2,790	0,827
Переслаивание аргиллитов с песчаниками	1	5	8,06	3,43	0,159	2,736	0,437
	2	8	7,56	3,24	0,185	2,700	0,594
	3	10	6,87	2,69	0,257	2,761	1,318
Переслаивание алевролитов с песчанниками	1	3	8,65	3,43	0,245	2,788	0,239
	2	2	8,55	3,37	0,251	2,805	0,588
	3	3	6,46	2,52	0,310	2,792	1,012
Переслаивание аргиллитов, алевролитов, песчаников	1	3	9,03	3,53	0,258	2,783	0,402
	2	3	8,77	3,51	0,245	2,786	0,629
	3	2	7,08	3,10	0,356	2,774	0,743
Фельэиты	1	2	8,23	3,45	0,243	2,630	0,330
	2	5	7,52	3,33	0,131	2,682	1,029
	3	2	6,36	2,76	0,155	2,679	1,178
Микродиориты	1	4	8,12	3,29	0,246	2,812	0,449
	3	4	5,88	2,26	0,290	2,829	2,235
Спессартиты	1	1	10,10	4,96	0,085	2,812	0,150
	3	2	9,01	3,65	0,232	2,885	1,390
Кварцевые порфиры	1	2	8,14	3,51	0,169	2,740	0,486
	3	5	7,08	3,18	0,134	2,720	0,661
Кузелиты	1	3	9,12	3,75	0,210	2,827	0,308
	3	4	7,52	3,00	0,248	2,798	0,705

Необходимо выполнить двухфакторный анализ Фридмана. Для решения использовать программу STATISTICA.

Каждый расчет проверяет гипотезу для одного из петрофизических свойств: модуля Юнга, модуля сдвига, коэффициента Пуассона, объемной массы, или эффективной пористости.

Указание

Заполнение таблицы исходными данными для случая проверки гипотезы эффективной пористости показано на рис. IV.7.

Для выполнения двухфакторного анализа Фридмана следует открыть меню Statistics программы STATISTICA и выбрать пункт Nonparametrics. В диалоговом окне Nonparametrics Statistics следует выбрать раздел Comparing multiple dep. samples (variables). В открывшемся диалоговом окне Friedman ANOVA by ranks следует выбрать переменные для исследования кнопкой Variables (рис. IV.8) и затем кнопкой Summary: Friedman ANOVA & Kendall’s concordance выполнить расчет. Результат выполнения дисперсионного анализа Фридмана приведен на рис. IV.9.

Обсудить результаты.

Рис. IV.7. Заполнение столбцов исходными данными

Рис. IV.8. Выбор имен переменных для исследования

Рис. IV.9. Результат двухфакторного дисперсионного анализа Фридмана

ЛАБОРАТОРНАЯ РАБОТА № V. ДВУМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ. РЕГРЕССИОННЫЙ АНАЛИЗ

Моделирование геологических образований и процессов как сложных природных систем часто вызывает необходимость совместного рассмотрения нескольких их свойств с целью выяснения общей структуры изучаемого объекта. Так, например, при изучении полезных ископаемых по керну скважин одновременно определяют мощность залежи, содержание в ней полезных компонентов, породообразующих элементов, значения эффективной пористости или различные другие свойства вмещающих пород и руд.

В одних случаях изучаемые свойства геологических объектов проявляются независимо друг от друга, а в других между ними могут быть выявлены более или менее отчетливые взаимосвязи.

Например, в редкометалльных пегматитах тантал и ниобий входят в состав только одного минерала – танталит-колумбита (Fe, Mn) (Nb, Та)₂О₆. Между содержаниями этих элементов в рудах всегда наблюдается прямая зависимость: чем больше тантала, тем больше ниобия, а между их содержаниями в мономинеральных фракциях – обратная. Это объясняется тем, что в рудах содержания обоих элементов прямо пропорциональны концентрациям рудного минерала, а в минерале тантал и ниобий изоморфно замещают друг друга в кристаллической решетке.

В других случаях для объяснения природы наблюдаемых зависимостей необходимо проследить длинную цепочку взаимозависимых процессов и явлений. Так, в результате обработки многолетних статистических данных о случаях тяжелого производственного травматизма на угольных шахтах было установлено, что их частота определенным образом связана с фазами луны. Эта на первый взгляд весьма странная связь объясняется влиянием положения луны на приливные силы, которые проявляются не только в гидросфере, но и в литосфере, и часто играют роль «спускового крючка» для таких явлений как горный удар, выбросы газа и т.п.

Часто связь между различными свойствами геологических объектов вообще не поддается объяснению с генетических или причинно-следственных позиций, так как наблюдаемые зависимости могут быть не связаны с геологическими процессами, а обусловлены методикой изучения геологических объектов или другими причинами. Так, например, существует зависимость между частотой обнаружения коренных рудных выходов и типом современных ландшафтов опоискованных площадей. Большинство коренных рудных выходов концентрируется в ландшафтных зонах эрозионного типа, а в аккумулятивных ландшафтах они обнаруживаются гораздо реже. Очевидно, что никаких причинно-следственных связей между процессами рудообразования и более поздними процессами формирования современных ландшафтов нет, а выявленная закономерность обусловлена тем, что в ландшафтных зонах аккумулятивного типа резко снижается эффективность поисков.

Изучение взаимозависимостей между значениями свойств геологических образований способствует более глубокому пониманию особенностей геологических процессов и выявлению факторов, влияющих на эффективность методов исследования геологических объектов. В ряде случаев оно позволяет получить количественные оценки некоторых свойств по значениям других, легко определяемых свойств. Так как изучаемые взаимозависимости имеют статистический характер и практически всегда отличаются от функциональных, для их изучения и описания используются двумерные и многомерные статистические модели.

ПРОВЕРКА ГИПОТЕЗ О НАЛИЧИИ КОРРЕЛЯЦИОННОЙ СВЯЗИ

Выявление корреляционных связей между различными свойствами геологических объектов способствует решению весьма широкого круга задач. Наиболее часто корреляционный анализ используется при изучении геологических процессов, разработке поисковых критериев факторов рудоконтроля, а также при выборе рациональных комплексов методов исследований при геологическом картировании, поисках и разведке месторождений.

Изучение геологических процессов может идти по-разному. В одних случаях первоначально создается гипотетическая модель процесса, на основе которой высказываются предположения о характере зависимостей между отдельными свойствами геологических образований, сформированных этим процессом. Затем выборочным методом производится определение этих свойств и статистическая обработка полученных наблюдений. Если гипотеза о наличии и характере корреляционной связи подтверждается, это служит косвенным подтверждением правомерности исходной геологической модели. В других случаях статистический анализ результатов наблюдений предшествует теоретическим включениям, а выявленные корреляционные связи учитываются при разработке детерминированных моделей, описывающих зависимости между геологическими явлениями и изучаемыми физическими, химическими, биологическими и другими факторами.

К задачам такого типа относятся:

• выявление парагенетических ассоциаций минералов и химических элементов в горных породах и рудах. Так, например, наличие корреляционных связей между петрогенными и редкими элементами способствует оценке роли процессов дифференциации магмы и ассимиляции ею вмещающих пород;

• изучение поведения химических элементов в процессе гипергенного и метасоматического изменения пород. Нарушение корреляционных связей, свойственных неизмененным породам и появление новых связей позволяет судить о подвижности химических элементов, устойчивости тех или иных минералов и общем характере геохимических процессов;

• палеогеографический анализ условий формирования осадочных пород. Так, например, выявление зависимостей между гранулярным и минеральным составом и степенью окатанности обломочного материала позволяет определять области сноса и границы бассейна осадконакопления при формировании определенных стратиграфических горизонтов;

• выяснение источников рудного вещества путем изучения корреляционной связи между концентрацией рудных элементов во вмещающих породах и рудах.

Для целенаправленного ведения геологоразведочных работ очень важно знать факторы, влияющие на размещение в недрах полезных ископаемых, – химический и минеральный составы вмещающих пород, их физико-механические свойства (эффективная пористость, трещиноватость и т.п.), элементы залегания рудовмещающих структур и т.д. Проверка гипотез о наличии корреляционной связи между ними свойствами и концентрацией полезного компонента позволяет оценить роль каждого из них и наметить участки, наиболее благоприятные для локализации оруденения. Выявление таких связей между составом пород и руд и их физическими свойствами –магнитностью, электропроводностью, плотностью, естественной радиоактивностью и т.п., позволяет выбрать наиболее информативные геофизические методы для геологического картирования и поисков полезных ископаемых.

Иногда практический интерес представляют сведения не о наличии, а об отсутствии корреляционной связи. Установлено, что для неизменных горных пород различного состава характерна прямая корреляция между плотностью и магнитной восприимчивостью. В метасоматически измененных породах эта связь не наблюдается. На этом эффекте основан оригинальный способ картирования метасоматитов.

Проверка гипотезы о наличии корреляционной связи обычно основана на том, что для двумерной нормально распределенной случайной величины XY при отсутствии корреляции между Х и Y коэффициент корреляции и корреляционное отношение равны нулю. Поэтому процедура проверки заключается в расчете выборочных оценок этих характеристик и оценке значимости их отличия от нуля.

Для оценки степени взаимосвязи наибольшее распространение получил коэффициент линейной корреляции (Пирсона), предполагающий нормальный закон распределения наблюдений.

Коэффициент корреляции – параметр, характеризующий степень линейной взаимосвязи между двумя выборками. Коэффициент корреляции изменяется от –1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорциональная зависимость). При значении 0 линейной зависимости между двумя выборками нет. Здесь под прямой зависимостью понимают зависимость, при которой увеличение или уменьшение значения одного признака ведет, соответственно, к увеличению или уменьшению второго. Например, при увеличении температуры возрастает давление газа, а при уменьшении – снижается (при постоянном объеме). При обратной зависимости увеличение одного признака приводит к уменьшению второго и наоборот. Примером обратной корреляционной зависимости может служить связь между температурой воздуха на улице и количеством топлива, расходуемого на обогрев помещения.

На практике коэффициент корреляции принимает некоторые промежуточные значения между 1 и –1. Для оценки степени взаимосвязи можно руководствоваться следующими эмпирическими правилами. Если коэффициент корреляции (r) по абсолютной величине (без учета знака) больше, чем 0,95, то принято считать, что между параметрами существует практически линейная зависимость (прямая – при положительном r и обратная – при отрицательном r). Если коэффициент корреляции r лежит в диапазоне от 0,8 до 0,95, говорят о сильной степени линейной связи между параметрами. Если 0,6 < r < 0,8, говорят о наличии линейной связи между параметрами. При r < 0,4 обычно считают, что линейную взаимосвязь между параметрами выявить не удалось.

Выборочная оценка коэффициента корреляции может быть рассчитана по формуле

,

где и – выборочные оценки средних значений случайных величин X и Y; S_x и S_y – выборочные оценки их стандартов; п – количество сравниваемых пар значений.

При расчетах вручную удобнее пользоваться формулой

Когда математическое ожидание выборочного коэффициента корреляции равно нулю, величина имеет распределение Стьюдента с n–2 степенями свободы. Если рассчитанное по этой формуле значение величины t превышает табличное значение критерия Стьюдента для принятой доверительной вероятности и числа степеней свободы n–2, гипотеза об отсутствии корреляционной связи отвергается.

Приближенная оценка коэффициента корреляции может быть получена графическим способом с помощью корреляционного поля точек. Поле точек разделяется на четыре квадранта линиями, соответствующими медианам величин Х и Y (см. рис. V.1). Для оценки коэффициента корреляции используется формула

r = (n₁ – n₂)/( n₁ + n₂).

где n₁ – число точек в квадрантах I и III, а n₂ – в квадрантах II и IV.

Если корреляционная связь отсутствует, то количество точек во всех квадрантах будет примерно одинаковым, а величина r – близка к нулю. В случае прямой корреляционной связи большинство точек попадет в квадранты III и I и r будет величиной положительной, а при обратной связи точки сконцентрируются преимущественно в квадрантах II и IV, а r будет величиной отрицательной. Так, например, приближенная оценка коэффициента корреляции соотношения объемная масса – содержание P₂O₅ (см. рис. V.1, а)

,

а для соотношения объемная масса – содержание A₂O₃

.

Рис. V.1. Корреляционные поля точек соотношений объемной массы Y (в т/м³) и содержаний Х (в %) P₂O₅ (а) Al₂O₃ (б) для апатит-нефелиновых руд месторождения Коашва

В Excel для вычисления парных коэффициентов линейной корреляции используется специальная функция КОРРЕЛ. Параметрами функции являются КОРРЕЛ(массив1,массив2), где:

• массив1 – это диапазон ячеек первой случайной величины;

• массив2 – это второй интервал ячеек со значениями второй случайной величины.

ПРИМЕР V.1

В рудах одного из полиметаллических месторождений присутствует золото, которое рассматривается как сопутствующий компонент. На одном из участков месторождения обнаружено, что корреляционная связь между концентрациями золота и свинца в рудах проявляется только при содержании свинца ниже 1,5 %, для богатых руд она практически отсутствует, а руды среднего качества характеризуются обратной корреляционной связью. Это объясняется тем, что в бедных вкрапленных рудах галенит первой генерации тесно ассоциирует с золотоносным пиритом, а высокие концентрации свинца в богатых рудах связаны с наличием более поздних незолотоносных кварц-карбонат-галенитовых прожилков.

Для подтверждения этой гипотезы и распространения ее на закономерности формирования всего месторождения необходимо провести анализ результатов опробования руд соседнего неизученного участка месторождения.

Требуется

Определить наличие корреляционной связи между золотом и свинцом в рудах на неизученном участке месторождения по выборке, представленной в таблице V.1.

Таблица V.1. Содержание свинца и золота в рудах полиметаллического месторождения

№ проб	Pb	Au	№ проб	Pb	Au	№ проб	Pb	Au
1	2,05	3,76	19	1,21	0,61	37	5,16	0,87
2	5,03	2,09	20	2,92	0,40	38	0,37	1,15
3	0,80	1,98	21	0,74	0,27	39	0,44	0,91
4	0,31	0,20	22	1,53	2,57	40	2,21	4,25
5	0,77	3,10	23	3,70	0,90	41	4,67	2,03
6	4,01	1,67	24	2,71	1,69	42	1,44	4,31
7	1,19	2,59	25	1,90	4,32	43	3,13	0,25
8	1,26	1,70	26	1,51	2,30	44	1,35	0,39
9	0,68	0,23	27	0,21	1,22	45	0,81	1,35
10	0,91	1,21	28	4,81	1,05	46	1,32	3,51
11	4,33	0,91	29	1,38	2,09	47	0,99	1,62
12	2,38	1,68	30	3,96	2,54	48	2,41	3,98
13	0,98	2,44	31	1,96	1,58	49	1,03	0,35
14	0,42	0,50	32	0,52	0,82	50	1,55	2,80
15	1,71	1,21	33	2,95	0,20	51	3,39	0,41
16	3,51	1,15	34	1,10	1,44	52	1,23	1,58
17	1,11	2,30	35	0,93	3,15	53	1,48	4,22
18	2,10	3,48	36	1,78	1,21	54	4,03	1,19

Решение

Откройте новый лист. Введите в ячейку А1 название Pb. Затем в ячейки А2:А55 – соответствующие значения концентраций в пробах. В ячейки В1:В55 введите название Au и значения для золота. Затем вычисляется значение коэффициента корреляции между выборками. Для этого табличный курсор установите в свободную ячейку (А56). На панели инструментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию КОРРЕЛ, после чего нажмите кнопку OK. Появившееся диалоговое окно КОРРЕЛ за серое поле мышью отодвиньте вправо на 1–2 см от данных (при нажатой левой клавише). Указателем мыши введите диапазон данных Pb в поле Массив 1 (А2:А55). В поле Массив 2 введите диапазон данных Au (В2:В55). Нажмите кнопку OK. В ячейке А56 появится значение коэффициента корреляции – число –0,04918. Значение коэффициента корреляции близко к нулю. Значит, можно говорить о том, что наличие корреляционной связи между золотом и свинцом в рудах на неизученном участке месторождения отсутствует.

При отсутствии значимой корреляционной связи между золотом и свинцом, проверить гипотезу о том, что такая связь может существовать только для бедных руд. Для этого из выборочных данных таблицы необходимо убрать пробы со значениями свинца более 1,5 %. Это можно проделать, используя функцию =ЕСЛИ(). В ячейку C2 запишите формулу =ЕСЛИ(A2<=1,5;A2;ЛОЖЬ), а в ячейку D2 – формулу =ЕСЛИ(A2<=1,5;B2;ЛОЖЬ). Скопируйте эти формулы методом автозаполнения в диапазоны C3:C55 и D3:D55 соответственно. В ячейку C56 поместите функцию =КОРРЕЛ(C2:C55;D2:D55). Значение коэффициента корреляции 0,54359. Значит, можно говорить о том, что наличие корреляционной связи между золотом и свинцом в рудах на неизученном участке месторождения существует только для бедных руд (со значениями свинца не более 1,5 %).

В Excel для вычисления корреляции также используется процедура Корреляция. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.

Для реализации процедуры необходимо:

• выполнить команду Сервис/Анализ данных;

• в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку OK;

• в появившемся диалоговом окне указать Входной интервал, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши. Входной интервал должен содержать не менее двух столбцов.

• в разделе Группировка переключатель установить в соответствии с введенными данными;

• указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить флажок в левое поле Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные.

• нажать кнопку OK.

Результаты анализа. В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует с самим собой.

Интерпретация результатов. Рассматривается отдельно каждый коэффициент корреляции между соответствующими параметрами. Его числовое значение оценивается по эмпирическим правилам, изложенным в разделе «Коэффициент корреляции». Отметим, что хотя в результате будет получена треугольная матрица, корреляционная матрица симметрична, и коэффициенты корреляции r_ij =r_ji.

ПРИМЕР V.2

Требуется

По условию предыдущего ПРИМЕРА V.1 определить наличие корреляционной связи между золотом и свинцом в рудах на неизученном участке месторождения по выборке, представленной в табл. V.1, используя процедуру Корреляция пакета Анализ данных.

Решение

Для выполнения корреляционного анализа введите в диапазон A2:B55 исходные данные. В ячейки A1 и B1 введите соответственно Pb и Au.

Затем в меню Сервис выберите пункт Анализ данных и далее укажите строку Корреляция. В появившемся диалоговом окне укажите Входной интервал A1:B55. Укажите, что данные рассматриваются по столбцам. Установите флажок в поле Метки в первой строке. Укажите выходной диапазон. Для этого поставьте флажок в левое поле Выходной интервал и в правое поле ввода Выходной интервал введите А57. Нажмите кнопку OK.

Результаты анализа. В выходном диапазоне получаем корреляционную матрицу. Подразумевается, что в пустых клетках в правой верхней половине таблицы находятся те же коэффициенты корреляции, что и в нижней левой (симметрично расположенные относительно диагонали). Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует с самим собой.

Интерпретация результатов. Из таблицы видно, что корреляция между свинцом и золотом в пробах равна –0,04918. Значит, можно говорить о том, что наличие корреляционной связи между золотом и свинцом в рудах на неизученном участке месторождения отсутствует.

При отсутствии значимой корреляционной связи между золотом и свинцом, следует проверить гипотезу о том, что такая связь может существовать только для бедных руд. Для этого из выборочных данных таблицы необходимо убрать пробы со значениями свинца более 1,5 %. Ввести в F1 и G1 соответственно Pb и Au. Ввести в столбец F только те значения, которые удовлетворяют условию отбора проб со значениями свинца не более 1,5 %. В столбец G – соответствующие значения для золота. Аналогично выполнить процедуру Корреляция, указав выходной интервал – F30.

Интерпретация результатов. Из таблицы видно, что корреляция между свинцом и золотом в пробах равна 0,54359. Можно говорить о наличии корреляционной связи между золотом и свинцом в рудах на неизученном участке месторождения.

Если во вкрапленных рудах существует значимая корреляционная связь между золотом и свинцом, следует провести регрессионный анализ для определения уравнения зависимости концентрации золота от содержания в рудах свинца.

РЕГРЕССИОННЫЙ АНАЛИЗ

При исследовании взаимосвязей между выборками помимо корреляции различают также и регрессию. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных. Соответственно, наряду с корреляционным анализом еще одним инструментом изучения стохастических зависимостей является регрессионный анализ.

Регрессионный анализ устанавливает формы зависимости между случайной величиной Y (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость обычно определяется некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров. В ходе регрессионного анализа на основании выборочных данных находят оценки этих параметров, определяются статистические ошибки оценок или границы доверительных интервалов и проверяется соответствие (адекватность) принятой математической модели экспериментальным данным.

В линейном регрессионном анализе связь между случайными величинами предполагается линейной. В самом простом случае в линейной регрессионной модели имеются две переменные Х и Y. И требуется по п парам наблюдений (X₁, Y₁), (X₂, Y₂), ..., (X_n, Y_n) построить (подобрать) прямую линию, называемую линией регрессии, которая «наилучшим образом» приближает наблюдаемые значения. Уравнение этой линии y = аx + b является регрессионным уравнением. С помощью регрессионного уравнения можно предсказать ожидаемое значение зависимой величины y, соответствующее заданному значению независимой переменной x.

Таким образом, можно сказать, что регрессионный анализ заключается в подборе графика и его уравнения для набора наблюдений. В регрессионном анализе все признаки (переменные), входящие в уравнение, должны иметь непрерывную, а не дискретную природу.

В случае, когда рассматривается зависимость между одной зависимой переменной Y и несколькими независимыми X₁, X₂, ..., X_m, говорят о множественной линейной регрессии.

В этом случае регрессионное уравнение имеет вид

y = a₀ + a₁x₁ + a₂x₂ + … + a_mx_m,

где a₀, a₁, a₂, …, a_m – требующие определения коэффициенты регрессии.

Мерой эффективности регрессионной модели является коэффициент детерминации R² (R-квадрат). Коэффициент детерминации (R-квадрат) определяет, с какой степенью точности полученное регрессионное уравнение описывает (аппроксимирует) исходные данные.

Исследуется также значимость регрессионной модели с помощью F-критерия (Фишера). Если величина F-критерия значима (р < 0,05), то регрессионная модель является значимой.

Достоверность отличия коэффициентов a₀, a₁, a₂, …, a_m от нуля проверяется с помощью критерия Стьюдента. В случаях, когда р > 0,05, коэффициент может считаться нулевым, а это означает, что влияние соответствующей независимой переменной на зависимую переменную недостоверно, и эта независимая переменная может быть исключена из уравнения.

В Excel экспериментальные данные аппроксимируются линейным уравнением до 16 порядка:

y = a₀ + a₁x₁ + a₂x₂ + … + a₁₆x₁₆,

где y – зависимая переменная, x₁, x₂, ..., x₁₆ – независимые переменные, a₀, a₁, a₂, …, a₁₆ – искомые коэффициенты регрессии.

Для получения коэффициентов линейной регрессии используется процедура Регрессия из пакета анализа. Кроме того, могут быть использованы функция ЛИНЕЙН, НАКЛОН и ОТРЕЗОК для получения параметров регрессионного уравнения и функция ТЕНДЕНЦИЯ и ПРЕДСКАЗ для получения предсказанных значений Y в требуемых точках. Не всегда полином дает лучшее приближение. Excel предоставляет возможность построить экспоненциальную регрессию. Для вычисления коэффициентов экспоненциальной регрессии в Excel существует функция ЛГРФПРИБЛ. Функция РОСТ для экспоненциальной регрессии позволяет получить значения Y в требуемых точках и имеет тот же смысл, что и функция ПРЕДСКАЗ для линейной регрессии.

Для реализации процедуры Регрессия необходимо:

• выполнить команду Сервис/Анализ данных;

• в появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия, указав курсором мыши и щелкнув левой кнопкой мыши. Затем нажать кнопку OK;

• в появившемся диалоговом окне задать Входной интервал Y, то есть ввести ссылку на диапазон анализируемых зависимых данных, содержащий один столбец данных. Для этого следует навести указатель мыши на верхнюю ячейку столбца зависимых данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

• указать Входной интервал X, то есть ввести ссылку на диапазон независимых данных, содержащий до 16 столбцов анализируемых данных. Для этого следует навести указатель мыши на поле ввода Входной интервал Х и щелкнуть левой кнопкой мыши, затем навести указатель мыши на верхнюю левую ячейку диапазона независимых данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней правой ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

• указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные;

• если необходимо визуально проверить отличие экспериментальных точек от предсказанных по регрессионной модели, следует установить флажок в поле График подбора;

• нажать кнопку OK.

Результаты анализа. Выходной диапазон будет включать в себя результаты дисперсионного анализа, коэффициенты регрессии, стандартную погрешность вычисления Y, среднеквадратичные отклонения, число наблюдений, стандартные погрешности для коэффициентов.

Интерпретация результатов. Значения коэффициентов регрессии находятся в столбце Коэффициенты и соответствуют:

• Y-пересечение – a₀;

• переменная Х₁ – a₁;

• переменная X₂ – a₂ и т.д.

В столбце P-Значение приводится достоверность отличия соответствующих коэффициентов от нуля. В случаях, когда P > 0,05, коэффициент может считаться нулевым, что означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.

Приводимое значение R-квадрат (коэффициент детерминации) определяет, с какой степенью точности полученное регрессионное уравнение аппроксимирует исходные данные. Если R-квадрат > 0,95, говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R-квадрат лежит в диапазоне от 0,8 до 0,95, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если R-квадрат < 0,6, принято считать, что точность аппроксимации недостаточна и модель требует улучшения (введения новых независимых переменных, учета нелинейностей и т.д.).

ПРИМЕР V.3

Требуется

Продолжив работу над ПРИМЕРОМ V.2, необходимо построить регрессионное уравнение, описывающее связь между золотом и свинцом в рудах на неизученном участке месторождения по выборке из таблицы V.1, используя процедуру Регрессия пакета Анализ данных.

Решение

1. Откройте рабочую книгу с результатами предыдущего ПРИМЕРА V.2.

2. В пункте меню Сервис выберите строку Анализ данных и далее укажите курсором мыши на строку Регрессия.

3. В появившемся диалоговом окне задайте Входной интервал Y. Для этого наведите указатель мыши на верхнюю ячейку столбца зависимых данных (G1), нажмите левую кнопку мыши и, не отпуская ее, протяните указатель мыши к нижней ячейке (G28), затем отпустите левую кнопку мыши. (Обратите внимание, что зависимые данные – это те данные, которые предполагается вычислять).

4. Так же укажите Входной интервал X, то есть введите ссылку на диапазон независимых данных F1:F28. (Независимые данные – это те данные, которые будут измеряться или наблюдаться).

5. Установите флажок в поле Метки в первой строке. Установите флажок в поле График подбора.

6. Далее укажите выходной диапазон. Для этого поставьте переключатель в положение Выходной интервал (наведите указатель мыши и щелкните левой кнопкой), затем наведите указатель мыши на правое поле ввода Выходной интервал и, щелкнув левой кнопкой мыши, указатель мыши наведите на левую верхнюю ячейку выходного диапазона (K3). Щелкните левой кнопкой мыши. Нажмите кнопку OK.

Результаты анализа. В выходном диапазоне появятся результаты и графики подбора и остатков.

Интерпретация результатов. В таблице Дисперсионный анализ оценивается общее качество полученной модели ее достоверность по уровню значимости критерия Фишера – р, который должен быть меньше, чем 0,05 (строка Регрессия, столбец Значимость F, в примере 0,00338372, то есть p =0,00338372 – модель значима, и степень точности описания моделью процесса – R-квадрат (вторая строка сверху в таблице Регрессионная статистика, в примере R-квадрат = 0,2954899. Поскольку R-квадрат < 0,95, можно говорить о невысокой точности аппроксимации – линейная модель не очень хорошо описывает явление.

Далее необходимо определить значения коэффициентов модели. Они определяются из таблицы в столбце Коэффициенты – в строке Y-пересечение приводится свободный член, в строках соответствующих переменных приводятся значения коэффициентов при этих переменных. В столбце p-значение приводится достоверность отличия соответствующих коэффициентов от нуля. В случаях, когда р > 0,05, коэффициент может считаться нулевым. Это означает, что соответствующая независимая переменная практически не влияет на зависимую переменную и коэффициент может быть убран из уравнения.

Отсюда выражение для определения концентрации золота в пробе по концентрации свинца будет иметь следующий вид: 0,0440856+1,7633983*концентрацияPb. Или, учитывая, что коэффициент для Y-пересечения незначим, – вид: 1,7633983*концентрацияPb.

Воспользовавшись полученным уравнением, можно рассчитать ожидаемую концентрацию золота в пробе по концентрации свинца. Например, для расчета концентрации золота при концентрации свинца равной 0,5 необходимо поставить табличный курсор в любую свободную ячейку (G35); ввести с клавиатуры знак =, щелкнуть указателем мыши по ячейке L19, ввести с клавиатуры знак +, щелкнуть по ячейке L20, ввести с клавиатуры знак * и число 0,5. В результате в ячейке G35 будет получена ожидаемая концентрация золота – 0,9257.

Результат приблизительно можно определить непосредственно по графику подбора. Наведите указатель мыши на график подбора и по появившейся надписи (см. рис. V.2) определите приближенно значение ожидаемой концентрация золота – 0,9610527.

Рис. V.2. Определение приближенного результата по графику подбора

ПРИМЕР V.4

Требуется

Заново решить задачу выбора линейной функции из ПРИМЕРА V.3, на этот раз с помощью функции ЛИНЕЙН электронных таблиц Excel, предназначенной для расчета линейной регрессии.

Решение

Скопируйте исходные данные (блок F1:G28 из решения ПРИМЕРА V.2) на новый рабочий лист в столбцы A и B. Для решения следует воспользоваться функцией

ЛИНЕЙН(известные_значения_y, известные_значения_x, конст, статистика).

В нашем случае известные_значения_y находятся в диапазоне B2:B28, а известные_значения_x находятся в диапазоне A2:A28. Два последние аргумента – логические. Если конст – ИСТИНА или опущено, то свободный член b в регрессионном уравнении может быть любым, а если конст – ЛОЖЬ, то b принудительно полагается равным нулю. Если последний аргумент статистика – ЛОЖЬ или опущен, то вычисляются только коэффициенты m и b, а если ИСТИНА, то выдаются дополнительные статистические характеристики. Вместо ИСТИНА и ЛОЖЬ в функции можно вводить аргументы 1 и 0, что намного удобнее.

Так как функция возвращает сразу несколько значений, формулу с этой функцией надо вводить как табличную. Если мы хотим ввести полную статистику, то надо выделить блок из пяти строк и двух столбцов. Выделить блок D2:E6, щелкнуть по кнопке со знаком равенства, в Мастере функций выбрать в категории Статистические функцию ЛИНЕЙН. Первым аргументом указать блок B2:B28, вторым аргументом – блок A2:A28, в третьем и четвертом поле ввода проставить 1. Не щелкать по кнопке OK, а нажать Ctrl+Shift+Enter (находясь в диалоговом окне)! Получим следующую таблицу (рис. V.3).

	D	E
2	1,763398	0,044086
3	0,544569	0,5412
4	0,29549	1,026895
5	10,48565	25
6	11,05725	26,36281

Рис. V.3. Результат расчета ПРИМЕРА V.4

В ячейку D2 записан коэффициент a, в E2 – коэффициент b. Под этими коэффициентами записаны стандартные ошибки для оценки этих коэффициентов.

В ячейку D4 записан так называемый коэффициент детерминации R². Этот коэффициент лежит на отрезке [0; 1]. Считается, что чем ближе этот коэффициент к 1, тем лучше регрессионное уравнение описывает зависимость.

В ячейке E4 находится стандартная ошибка для оценки y. В ячейку D5 записано значение F-статистики, а в E5 – количество степеней свободы. Число степеней свободы нужно для расчета критических значений F-статистики.

В последней строке таблицы записаны регрессионная сумма квадратов (11,05725) и остаточная сумма квадратов (26,36281). Последнее число – это сумма квадратов остатков.

Уравнение регрессии имеет вид 0,0440856+1,7633983*концентрацияPb.

ЗАДАЧА V.1

Указание

Наиболее важными для нас, естественно, являются коэффициенты a и b. Их можно вычислить с помощью функций НАКЛОН и ОТРЕЗОК, не прибегая к функции ЛИНЕЙН. Названия этих функций отвечают геометрическому смыслу коэффициентов регрессии: a – это тангенс угла наклона прямой регрессии, а b – отрезок, отсекаемый этой прямой на оси ординат. Вычислить для ПРИМЕРА V.4 коэффициенты a и b с помощью этих функций.

ПРИМЕР V.5

Требуется

По данным предыдущего ПРИМЕРА V.4 с помощью функции ЛИНЕЙН программы Excel построить квадратичную регрессию Y = a₀ + a₁X + a₂X².

Решение

Постановка задачи выглядит на первый взгляд парадоксально. Ведь функция ЛИНЕЙН даже по своему названию предназначена для отыскания именно линейной регрессии. Но в уравнение регрессии dx² +ex+f коэффициенты входят линейно.

Сейчас x-данные занимают диапазон A1:A28, а y-данные – диапазон B1:B28. Нужно ввести новый фактор: x². Для этого скопировать диапазон A1:B28 в диапазон G1:H28 и переместить H1:H28 вправо, в столбец I. В ячейку H2 ввести формулу =G2^2. Эту формулу скопировать методом автозаполнения в диапазон H2:H28. Для функции ЛИНЕЙН (со статистикой) нужно выделить блок, состоящий из пяти строк (для статистики) и трех столбцов (для коэффициента перед x², для коэффициента перед x, для свободного члена – коэффициенты идут в обратном порядке по сравнению со столбцами исходных данных). Ввести функцию в K2:M6. В итоге должен получиться результат (рис. V.4).

	K	L	M
2	1,6555527	-1,091662	1,0504107
3	1,5657128	2,7542427	1,094205
4	0,326849	1,0244787	#Н/Д
5	5,8266084	24	#Н/Д
6	12,23071	25,189357	#Н/Д

Рис. V.4. Результат расчета ПРИМЕРА V.5

Коэффициент детерминации R² принял значение 0,326849. Следовательно, данная модель несколько лучше описывает результаты отбора. Итак, введем в J2 формулу =G2*$L$2+H2*$K$2+$M$2 и скопируем ее вниз.

Уравнение регрессии имеет вид: 1,0504107–1,091662*концентрацияPb+1,655527*концентрацияPb^2.

ЗАДАЧА V.2

Требуется

По результатам предыдущих ПРИМЕРОВ V.4 и V.5 построить графики линейной и квадратичной регрессии.

Рис. V.5. Графики линейной и квадратичной регрессии

ПРИМЕР V.6

Требуется

По данным ПРИМЕРА V.1, используя пакет Statistica:

1) определить наличие корреляционной связи между золотом и свинцом в рудах на неизученном участке месторождения по выборке, представленной в табл. V.1;

2) при наличии корреляционной связи рассчитать уравнение зависимости содержания золота от свинца в рудах.

Решение

1. Создать файл данных в программе Statistica.

2. Провести корреляционный анализ всей выборки. Для этого в меню с основными процедурами Statistics выбрать Basic Statistics/Tables, а в появившемся его меню – Correlation matrices.

В появившемся диалоговом окне Product-Moment and Partial Correlations: нажать кнопку OneVariable List и в диалоговом окне Select the variables for the analysis нажать кнопку Select All (см. рис. V.6). Далее нажать OK.

Вернувшись в диалоговое окно Product-Moment and Partial, нажать на вкладке Quick кнопку Summary: Correlation Matrix и результатом будет – расчет корреляционной матрицы (см. ПРИМЕР V.2) – рис. V.7.

Значение коэффициента корреляции близко к нулю. Значит, можно говорить о том, что наличие корреляционной связи между золотом и свинцом в рудах на неизученном участке месторождения отсутствует.

Рис. V.6. Выбор данных для расчета корреляционной матрицы

Рис. V.7. Результат расчета корреляционной матрицы

3. При отсутствии значимой корреляционной связи между золотом и свинцом, проверить гипотезу о том, что такая связь может существовать только для бедных руд. Для этого из выборочных данных таблицы необходимо убрать пробы со значениями свинца более 1,5 %. Вначале имеющийся файл данных с таблицей необходимо сохранить под другим именем. Затем удалить ненужные ячейки. По обновленной таблице только с вкрапленными рудами провести корреляционный анализ между золотом и свинцом.

Аналогично п. 2 произвести расчет корреляционной матрицы – см. рис. V.8.

В диалоговом окне Product-Moment and Partial Correlations: нажать на вкладке Quick кнопку Scatterplot matrix for selected variables и результатом будут графическое изображение корреляции (рис. V.9).

Рис. V.8. Результат расчета корреляционной матрицы

Рис. V.9. Графическое изображение корреляции

Так как во вкрапленных рудах существует значимая корреляционная связь между золотом и свинцом, следует провести регрессионный анализ для определения уравнения зависимости концентрации золота от содержания в рудах свинца. Для этого в начальном меню StatisticS выбираем Multiple Regression.

В открывшемся диалоговом окне Multiple Linear Regression нажимаем кнопку Variables и устанавливаем, как показано на рис. V.10 в открывшемся диалоговом окне Select depended and independed variables lists:, зависимую и независимую переменные. Далее нажимаем OK.

Рис. V.10. Установка зависимой и независимой переменных для регрессионного анализа

Вернувшись в диалоговое окне Multiple Linear Regression, нажать OK.

Результатом будет Multiple Regression Results: – см. рис. V.11.

Далее, в этом диалоговом окне Multiple Regression Results:, нажать кнопку Summary: Regresion Results и получим – см. на рис. V.12 – таблицу статистик, в которой в столбце В указаны коэффициенты регрессии: 1,763398 – коэффициент a и 0,044086 – коэффициент b; p-level – уровень значимости для каждого коэффициента; beta – коэффициент корреляции.

Полученное уравнение регрессии дает представление о закономерностях в изучаемой выборке, где проанализированы как свинец, так и золото, но его можно использовать в дальнейшем для расчета прогнозной концентрации золота в пробах, по которым имеются лишь данные по содержанию свинца.

Рис. V.11. Multiple Regression Results

Рис. V.12. Таблица результатов Regresion Results

ЗАДАЧА V.3

На территории шахтного поля литохимическим расчетом на основе данных о химическом составе золы 54 проб углей, отобранных из керна геологоразведочных скважин, было определено содержание гидрослюды в углях. Однако для большого числа скважин химический состав золы вообще не определялся, либо оказался утерян, а сохранились лишь данные по зольности этих углей. Предполагается высокая корреляция между содержанием гидрослюды в углях и зольностью, что позволит оперировать уже имеющимися данными по зольности.

Для подтверждения этой гипотезы и распространения её на всё шахтное поле необходимо провести корреляционный анализ.

Требуется

1) определить наличие корреляционной связи между зольностью и содержанием гидрослюды в угле по выборке, представленной в табл. V.2;

2) при наличии корреляционной связи рассчитать уравнение зависимости содержания гидрослюды в угле от зольности.

Таблица V.2. Содержание гидрослюды и зольность углей

№ проб	Зольность, %	Гидрослюда в угле	№ проб	Зольность, %	Гидрослюда в угле
1	28,1	7,05	28	10,1	1,96
2	15,4	2,62	29	14,0	2,07
3	12,8	3,34	30	19,4	6,35
4	11,1	1,96	31	13,9	2,42
5	10,4	2,37	32	8,1	4,19
6	9,3	2,22	33	10,1	1,02
7	17,8	2,88	34	10,2	3,73
8	13,7	2,53	35	11,8	3,21
9	17,8	6,94	36	23,8	4,51
10	15,2	3,78	37	9,3	2,70
11	16,4	2,61	38	24,5	4,90
12	12,8	1,41	39	15,7	3,94
13	12,3	1,82	40	16,1	4,92
14	13,9	1,78	41	7,5	2,12
15	16,1	2,68	42	12,4	2,53
16	9,6	3,27	43	13,7	6,43
17	6,6	0,57	44	9,0	2,00
18	17,6	3,50	45	10,9	4,23
19	10,9	1,72	46	21,3	2,34
20	8,0	2,20	47	8,3	2,03
21	12,1	2,88	48	11,8	3,02
22	8,1	2,05	49	24,0	10,52
23	13,7	1,60	50	6,9	0,48
24	17,6	9,77	51	7,0	3,44
25	12,5	3,68	52	47,9	27,67
26	15,4	4,55	53	42,3	24,92
27	12,5	3,4	54	41,5	9,90

Решение

1. Создать файл данных, используя процедуру программы Statistica.

2. Провести корреляционный анализ всей выборки. Для этого в меню с основными процедурами Statistics выбрать Basic Statistics/Tables, а в появившемся его меню – Correlation matrices.

3. Если существует значимая корреляционная связь между зольностью и содержанием гидрослюды в угле, провести регрессионный анализ, для определения уравнения зависимости содержания гидрослюды в угле от зольности. Для этого в начальном меню StatisticS выбираем Multiple Regression.

Если не удается проверить гипотезу о соответствии эмпирического распределения определенному закону из-за малого количества данных (или распределения существенно отличаются от нормального закона и не поддаются нормализации), то для проверки гипотезы о наличии корреляционной связи можно использовать ранговый коэффициент корреляции Спирмена. Его расчет основан на замене выборочных значений исследуемых случайных величин их рангами в порядке возрастания. При этом предполагается, что если между значениями случайных величин нет корреляционной зависимости, то ранги этих величин тоже будут независимыми. Выражение для расчета рангового коэффициента корреляции имеет вид

где d_i – разность рангов сопряженных значений изучаемых величин x_i и y_i, п – количество пар в выборке.

Если ранги значений Х и Y являются независимыми случайными величинами, то выборочная оценка r распределена нормально с математическим ожиданием 0 и дисперсией 1/(n –1) и может быть определена по таблице приложения I или с помощью функции Excel НОРМСТОБР.

Для проверки значимости рангового коэффициента корреляции можно использовать величину , где Z(P) – значение обратной функции нормального распределения при доверительной вероятности P.

Если расчетное значение коэффициента Спирмена (r) больше критического ( ), то гипотеза о независимости исследуемых величин отвергается.

ПРИМЕР V.7

При проведении гидрогеологических изысканий по одному из профилей буровых скважин были выполнены опытные электроразведочные работы. Для оценки эффективности этого метода необходимо знать, существует ли зависимость между электрическим сопротивлением пород (ρ_x) и относительной мощностью горизонта гравийно-галечных отложений (m_r), к которым приурочены основные водоносные горизонты. В профиле пробурено всего 12 скважин (табл. V.3).

Требуется

Для проверки гипотезы о наличии корреляционной связи между значениями ρ_x и m_r воспользоваться ранговым коэффициентом корреляции Спирмена.

Решение

В ячейки A1, B1 и D1 введите названия № скв., m_r и ρ_x соответственно. Введите в столбцы A, B, D номера скважин и значения в процентах m_r и ρ_x соответственно из табл V.3. Скопируйте значения столбцов B и D в столбцы I и J. Отсортируйте через меню Данные/Сортировка… в порядке возрастания сначала столбец I, а затем столбец J. В столбце K проставьте ранги от 1 до 12 через меню Правка/Заполнить/Прогрессия… . В ячейку C2 запишите формулу =ВПР(B2;$I$2:$K$13;3;0), скопируйте ее методом автозаполнения в ячейки C2:C13. В ячейку E2 запишите формулу =ВПР(D2;$J$2:$K$13;2;0), скопируйте ее методом автозаполнения в ячейки E2:E13. В столбцах C и E рассчитаны ранги значений электрического сопротивления пород (ρ_x) и относительной мощности горизонта гравийно-галечных отложений (m_r). В ячейке F2 запишите формулу =C2-E2 и скопируйте ее методом автозаполнения в ячейки F2:F13. Это d_i – разность рангов сопряженных значений изучаемых величин x_i и y_i. В ячейке G2 запишите формулу =F2^2 и скопируйте ее методом автозаполнения в ячейки G2:G13. В ячейке G14 рассчитайте сумму =СУММ(G2:G13). В ячейке B15 запишите n – количество пар в выборке. В ячейке B16 рассчитайте значение рангового коэффициента корреляции . В ячейке B17 запишите значение величины обратной функции нормального распределения Z для доверительной вероятности 0,95, которое равно 1,64 (см. приложение I), а в ячейке B18 рассчитайте критическое значение рангового коэффициента корреляции при этой доверительной вероятности и объеме выборки в 12 значений, которое будет .

Значение величины обратной функции нормального распределения Z для доверительной вероятности 0,95 может быть определено с помощью формулы =НОРМСТОБР(0,05).

Окончательный вид листа электронных таблиц Excel при расчете критерия Спирмена представлен на рис. V.13.

Расчетное значение рангового коэффициента корреляции больше критического, что свидетельствует о статистически значимой корреляционной связи между значениями относительной мощности и электрическим сопротивлением горизонта гравийно-галечных отложений. Следовательно, данный геофизический метод можно рекомендовать для широкого использования при проведении гидрогеологических изысканий в данном районе.

Таблица V.3. Результаты вычисления рангового коэффициента корреляции для значений m_r и ρ_x

№ скв.	mr		ρx		di
	значение, %	ранг	значение, %	ранг
1	67	9	253	10	-1	1
2	80	12	115	7	5	25
3	40	5	126	8	-3	9
4	24	2	82	6	-4	16
5	25	3	66	5	-2	4
6	38	4	25	1	3	9
7	18	1	44	3	-2	4
8	72	10	180	9	1	1
9	44	6	32	2	4	16
10	51	8	319	11	-3	9
11	76	11	421	12	-1	1
12	50	7	51	4	3	9

Рис. V.13. Расчет критерия Спирмена

При наличии нескольких пар с одинаковыми значениями вычисление коэффициента корреляции несколько усложняется:

,

где и – поправки на повторяющиеся содержания первого и второго элемента соответственно, вычисляемые из выражения

где – количество данных с повторяющимися содержаниями элемента; m – количество таких групп с повторяющимися содержаниями элемента.

Примечание

Синтаксис функции ВПР(искомое_значение; таблица; номер_столбца; интервальный_просмотр).

Искомое_значение – это значение, которое должно быть найдено в первом столбце массива. Искомое_значение может быть значением, ссылкой или текстовой строкой.

Таблица – таблица с информацией, в которой ищутся данные. Можно использовать ссылку на интервал или имя интервала, например БазаДанных или Список.

• Если интервальный_просмотр имеет значение ИСТИНА, то значения в первом столбце аргумента «таблица» должны быть расположены в возрастающем порядке: ..., -2, -1, 0, 1, 2, ..., A-Z, ЛОЖЬ, ИСТИНА; в противном случае функция ВПР может выдать неправильный результат. Если интервальный_просмотр имеет значение ЛОЖЬ, то таблица не обязана быть отсортированной.

• Данные можно упорядочить следующим образом: в меню Данные выбрать команду Сортировка и установить переключатель По Возрастанию.

• Значения в первом столбце аргумента таблица могут быть текстовыми строками, числами или логическими значениями.

• Текстовые строки сравниваются без учета регистра букв.

Номер_столбца – это номер столбца в массиве таблица, в котором должно быть найдено соответствующее значение. Если номер_столбца равен 1, то возвращается значение из первого столбца аргумента таблица; если номер_столбца равен 2, то возвращается значение из второго столбца аргумента таблица и так далее. Если номер_столбца меньше 1, то функция ВПР возвращает значение ошибки #ЗНАЧ!; если номер_столбца больше, чем количество столбцов в аргументе таблица, то функция ВПР возвращает значение ошибки #ССЫЛ!.

Интервальный_просмотр – это логическое значение, которое определяет, нужно ли, чтобы ВПР искала точное или приближенное соответствие. Если этот аргумент имеет значение ИСТИНА или опущен, то возвращается приблизительно соответствующее значение; другими словами, если точное соответствие не найдено, то возвращается наибольшее значение, которое меньше, чем искомое_значение. Если этот аргумент имеет значение ЛОЖЬ, то функция ВПР ищет точное соответствие. Если таковое не найдено, то возвращается значение ошибки #Н/Д.

• Если ВПР не может найти искомое_значение и интервальный_просмотр имеет значение ИСТИНА, то используется наибольшее значение, которое меньше, чем искомое_значение.

• Если искомое_значение меньше, чем наименьшее значение в первом столбце аргумента таблица, то функция ВПР возвращает значение ошибки #Н/Д.

• Если ВПР не может найти искомое_значение и интервальный_просмотр имеет значение ЛОЖЬ, то ВПР возвращает значение ошибки #Н/Д.

Коэффициент корреляции может служить надежной характеристикой стохастической связи лишь в условиях линейности обоих уравнений регрессии. В равной мере это относится и к ранговому коэффициенту корреляции Спирмена. Однако в геологической практике зависимость между свойствами изучаемых объектов часто отличается от линейной. Так, например, в рудах одного из свинцовых месторождений присутствует золото, которое рассматривается как сопутствующий полезный компонент. Линейная прямая корреляционная связь между концентрациями золота и свинца в рудах проявляется только при содержаниях свинца ниже 1,5%, для богатых руд она практически отсутствует, а руды среднего качества характеризуются обратной корреляционной связью (рис. V.14). Это объясняется тем, что в бедных вкрапленных рудах галенит первой генерации тесно ассоциирует с золотоносным пиритом, а высокие концентрации свинца в богатых рудах связаны с наличием более поздних незолотоносных кварц-карбонат-галенитовых прожилков.

Рис. V.14. Зависимость между содержанием золота и свинца в рудах свинцового месторождения

О характере связи судят по виду эмпирических линий регрессии. Если они заметно отличаются от прямой, гипотезу о наличии корреляционной связи следует проверить с помощью отношения.

Для вычисления оценок корреляционных отношений выборочные данные группируются в классы по значениям одного из исследуемых свойств. По каждому классу рассчитываются групповые средние , или , и оценки стандартных отклонений групповых средних и по формулам

; (V.1)

где n_i – число наблюдений в i-ой группе; т – число групп; N – общее число наблюдений.

Выборочные значения корреляционных отношений определяются

; ,

где S_x и S_y – оценки общего стандартного отклонения исследуемых случайных величин.

Статистическая значимость отличия корреляционного отношения от нуля проверяется с помощью критерия

. (V.2)

При равенстве истинного корреляционного отношения нулю величина распределена нормально с математическим ожиданием 0 и дисперсией 1, что позволяет определять критические значения для заданных доверительных вероятностей по таблицам нормального распределения. Если расчетное значение превышает критическое, гипотеза об отсутствии корреляционной связи отвергается. Аналогично проверяется гипотеза о наличии корреляционной связи по .

ЗАДАЧА V.4

Требуется

Проверим гипотезу о наличии корреляционной связи между содержаниями золота и свинца в рудах упомянутого выше свинцового месторождения.

Указание

С помощью коэффициента корреляции устанавливается отсутствие связи между содержаниями золота и свинца в рудах свинцового месторождения (ПРИМЕР V.1). Однако, учитывая нелинейный характер графика линии регрессии (см. рис. V.14), гипотезу о наличии корреляционной связи следует проверить повторно по корреляционному отношению. С этой целью по формуле (V.1) рассчитываем стандартное отклонение групповых средних: . Предварительно выборочные данные следует сгруппировать в классы по X, которые указаны во втором столбце табл. V.4. Числа наблюдений в каждой группе n_i (пятый столбец табл. V.4.) могу быть рассчитаны с помощью функции Excel ЧАСТОТА или с помощью функции Excel СЧЕТ в каждой группе, групповые средние , – с помощью функций Excel СРЗНАЧ в каждой группе. Для расчета необходимо также рассчитать разности (четвертый столбец табл. V.4.)) и произведения (шестой столбец табл. V.4.)).

Таблица V.4. Расчет корреляционного отношения между содержаниями золота (Y) и свинца (X)

№ п/п	Классы группирования по X
1	0,20-0,70			7
2	0,71-1,20			12
3	1,21-1,70			11
4	1,71-2,20			6
5	2,21-2,70			3
6	2,71-3,20			4
7	3,21-3,70			3
8	3,71-4,20			3
9	4,21-4,70			2
10	4,71-5,20			3

Затем следует рассчитать стандартное отклонение величины у по формуле =СТАНДОТКЛОН(), которое равно 1,21.

Оценка корреляционного отношения для содержания золота по содержанию свинца составит

.

Для проверки статистической значимости отличия корреляционного отношения от нуля по формуле (V.2) рассчитываем значение величины , которое равно 6,21.

Размещение расчетов на рабочем листе Excel – см. рис. V.15.

Рис. V.15. Фрагмент расчета корреляционного отношения

Поскольку критическое значение величины при доверительной вероятности 0,95 составляет 1,64 (см. приложение I), гипотеза об отсутствии корреляционной связи между исследуемыми величинами отвергается. Следовательно, между этими величинами существует статистически значимая нелинейная корреляционная связь.

Значение величины функции нормального распределения с математическим ожиданием 0 и дисперсией 1 может быть определено с помощью формулы =НОРМСТОБР(0,05).

ИСПОЛЬЗОВАНИЕ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ ДЛЯ ПРЕДСКАЗАНИЯ СВОЙСТВ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ

Если для двух величин на основании представительной выборки доказано наличие корреляционной связи, определен ее вид и подобрано описывающее его уравнение, то создается возможность прогноза значений одной из случайных величин по значениям другой.

Решение задач данного типа основано на построении эмпирических линий регрессии или расчете их аналитических выражений – уравнений регрессии. Для правильного решения таких задач необходимо не только оценить силу корреляционной связи, но и выявить ее характер. Поэтому приближенный способ проверки гипотезы о линейности связи по виду эмпирической линии регрессии в данном случае обычно дополняется аналитическими расчетами. Аналитический способ проверки гипотезы о линейности связи основан на том, что при ее наличии коэффициент корреляции и корреляционное отношение совпадают по абсолютной величине.

Подходящим критерием для проверки данной гипотезы является критерий Фишера

(V.3)

где – корреляционное отношение признака Y по классам группирования X; т – число классов группирования; N –количество пар значений XY.

Полученные значения F сравниваются с табличными значениями F_кр для заданного уровня значимости α при f₁ = (m–2) и f₂ = (N–m) степенях свободы. Корреляция должна считаться нелинейной, если F > F_кр.

ЗАДАЧА V.5

Требуется

Проверить гипотезу о линейности корреляционной связи между содержаниями золота и свинца в рудах свинцового месторождения (исходные данные см. ЗАДАЧУ V.4) с помощью критерия Фишера.

Указание

По формуле (V.3) рассчитаем критерия Фишера, который равен .

Табличное значение критерия Фишера для доверительной вероятности 0,95 при 8 и 44 степенях свободы равно около 3,0 (см. приложение X). Критические значения критерия Фишера могут быть вычислены в программе Excel с помощью функция FРАСПОБР для заданных вероятности и степеней свободы.

Следовательно, гипотеза о линейности корреляционной связи между содержаниями данных компонентов в руде отвергается.