2.1.3 Алгоритм Брезенхема креслення кола

У растр потрiбно розкладати не тiльки лiнiйнi, а й iншi, складнiші функцiї. Розкладання у растр конiчних перерiзiв, тобто кола, елiпса, параболи, гiперболи, розглядалося у значної кiлькостi робiт ([14], [15], [16], [17]). Найбiльшу увагу приділяли колу ([18], [19], [20], [21]).Найбiльш ефективний i нескладний алгоритм був запропонований Брезенхемом [22]. Для початку зауважимо, що можна генерувати тiльки одну восьму частину кола (наприклад, перший октант з кутом вiд 0 до 45 градусiв). Інші частини одержуємо послiдовними симетрiями (вiдносно прямої y=x , потім вiдносно прямої x=0 i нарештi вiдносно прямої y=0).Для побудови алгоритму розглянемо першу чверть (квадрант) кола з центром в початку координат. Зауважимо, що при початку роботи алгоритму з точки (0,R) i генерацiї точок кола за годинниковою стрiлкою у першому квадрантi y-координати згенерованих точок, є монотонно спадною функцією вiд аргументу x. Будемо вважати, що центр кола знаходиться у точцi (0,0) i радiус R>0 є величина цiла.

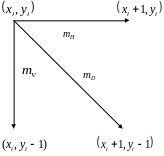
Для будь-якої точки кола при генеруваннi за напрямом стрiлки годинника iснує лише три можливостi обрати наступний пiксел, що наближатиме коло найлiпшим чином:

Рис.1. Вибiр пiкселiв у першому квадрантi

На рис.1. цi напрямки позначенi вiдповiдно m_H, m_D, і m_V. Алгоритм вибирає той пiксел, для якого є найменшим квадрат вiдстанi мiж одним з цих пiкселiв i колом, тобто вибирає мiнiмум з наступних чисел

У околi точки (x_i,y_i) можливi лише п'ять типiв перетину кола з сіткою растра:

Випадок 1. Коло пройде мiж точками (x_i+1,y_i) i (x_i+1,y_i-1).

Випадок 2. Коло пройде мiж точками (x_i+1,y_i) i (x_i+1,y_i+1).

Випадок 3. Коло пройде мiж точками (x_i,y_i-1) i (x_i+1,y_i-1).

Випадок 4. Коло пройде мiж точками (x_i-1,y_i-1) i (x_i, y_i-1).

Випадок 5. Коло пройде через точку (x_i+1,y_i-1).

Позначимо через рiзницю мiж квадратами вiдстаней вiд центра кола до пiксела (x_i+1,y_i-1) i вiд центра кола до точки на колi, тобто .

Як у алгоритмi Брезенхема для вiдрiзка, бажано при обраннi нового пiксела використовувати лише знак похибки . Розглянемо алгоритм пiд цим кутом зору.

1. Випадок, коли <0. При <0 дiагональна точка (x_i+1,y_i-1) знаходиться всерединi кола, тобто маємо випадки 1 або 2. Звiсно, що потрiбно вибрати або пiксел (x_i+1,y_i), тобто m_H, або пiксел (x_i+1,y_i-1), тобто m_D.

Розглянемо спочатку випадок 1. Знайдемо рiзницю квадратiв вiдстаней від кола до пiкселiв у горизонтальному m_H i дiагональному m_D напрямках:

При <0 вiдстань вiд кола до дiагонального пiксела (величина m_D) бiльшa нiж до горизонтального (величина m_H). Тому

при 0 вибираємо mH (у точку (xi+1, yi)), інакше вибираємо mD ( у точку (xi+1, yi-1))

(3)

Зауважимо, що у випадку 1: (x_i+1)² +y_i²-R² 0, (x_i+1)² +(y_i-1)²-R² 0 тому що дiагональний пiксел (x_i+1,y_i-1) завжди лежить всерединi кола, а горизонтальний пiксел (x_i+1,y_i) - зовнi. Тому можна рахувати за формулою

= (x _i +1)² + y _i ² – R ² + (x _i +1) ²+(y _i - 1)²-R ²

=2(x _i +1) ² + 2 y_i ²-1²-2 R ²-2 y _i -1=2 ( + y_i)-1

У випадку 2 потрiбно вибрати горизонтальний пiксел (x_i+1,y_i) тому, що y є монотонно спадна функцiя вiд x. При цьому горизонтальний (x_i+1,y_i) i дiагональний (x_i+1,y_i-1) пiкселi лежать у серединi кола.

Тодi (x_i + 1) ²+ y _i ² – R ² <0, (x _i + 1) ² + (y _i - 1) ² – R ²<0 i

= - (x _i + 1) ² – y _i ² + R ² + (x _i + 1) ² + (y _i - 1) ² - R ²= - 2y_i +1<0.

Тому дiє правило (3).

2. Випадок, коли >0. При >0 дiагональна точка (x_i+1,y_i-1) знаходиться зовнi кола, тобто одержуємо випадки 3 i 4 (потрiбно вибрати або пiксел (x_i+1,y_i-1), тобто m_D, або пiксел (x_i,y_i-1), тобто m_V). Знайдемо рiзницю квадратiв вiдстаней вiд кола до пiкселiв у дiагональному m_D i вертикальному m_V напрямках:

При '<0 вiдстань вiд кола до вертикального пiксела (x_i, y_i-1) бiльше нiж вiдстань до дiагонального (x_i+1, y_i-1) пiксела. Тому формулюємо наступне правило вибору

при ’ 0 вибираємо mD ( у точку (x i+ 1, yi - 1)) інакше вибираємо mV (у точку (xi, yi-1))

(4)

Перевiрка компонент ' для випадку 3 дає (x_i + 1) ² + ( y_i - 1) ² – R ² 0,

x _i ² + (y _i + 1) ² – R ² < 0 тому, що у цьому випадку дiагональний пiксел

(x _i + 1 , y _i - 1) лежить зовнi кола, а вертикальний пiксел (x _i , y_i - 1) -- у серединi кола. Звідси

’= (x _i +1)² + (y _i - 1) ² – R ² + x _i ²+(y _i - 1)²-R ²

=2(x _i +1) ² + 2( y_i - 1)² - 2 R ² + (y _i -1)² – 2 x_i - 1=2 ( + x_i)-1

У випадку 4 потрiбно вибирати вертикальний пiксел (x_i, y_i-1) тому, що y є монотонно спадна функція вiд x. При цьому (x_i + 1)²(y_i -1)² - R²>0,

x_i² + (y_i - 1)² - R²>0 тому, що обидва пiкселя знаходяться зовнi кола. Звiдси '>0, тобто дiє правило (4)

3. Випадок, коли =0. При =0 маємо випадок 5, тобто коли дiагональний пiксел (x_i+1,y_i-1) належить до кола. Перевiрка компонент виразу дає (x_i+1)²+y_i²-R²>0, (x_i+1)²+(y_i-1)²-R²=0.

Тому =(x_i+1)²+y_i²-R²>0 i вибираємо дiагональний пiксел (x_i+1)+(y_i-1)²-R², що збiгається з правилом (3). Перевірка компонент виразу ' дає (x_i+1)²+(y_i-1)²-R²=0, x_i²+(y_i-1)²-R²=0, x_i²+(y_i-1)²-R² 0.

Тому '=(x_i+1)²+(y_i-1)²-R²>0 i вибираємо дiагональний пiксел (x_i+1,y_i-1), що збiгається з правилом (4).

Таким чином, випадок, коли =0 можна обробляти як за випадком, коли <0, так i за випадком, коли >0.

Знайдемо рекурентнi спiввiдношення для реалiзацiї крокiв алгоритму. Розглянемо рiзнi випадки.

Горизонтальний крок m_H до пiкселя (x_i+1,y_i): x_i+1=x_i+1, y_i+1=y_i,

_i+1=(x_i+1 + 1) ² + (y_i+1 - 1) ²- R ²=x_i+1 ² + 2x_i+1 + 1 + (y_i-1) ² – R ²=

= (x_i+1) ² + (y _i-1)² – R ² + 2x_i+1 + 1= _i + 2x_i+1 + 1.

Дiагональний крок m_D до пiкселя (x_i+1,y_i-1):x_i+1=x_i+1, y_i+1=y_i-1,

_i+1=(x_i+1 + 1) ² + (y_i+1 - 1) ² – R ² = x_i+1 ² + 2x_i+1 + 1 + y_i+1² - 2y_i+1 + 1 – R ² =

= (x_i + 1)² + (y_i - 1)² – R ² + 2x_i+1 - 2y_i+1 + 2 = _i + 2x_i+1 - 2y_i+1 + 2.

Вертикальний крок m_V до пiкселя (x_i, y_i-1): x_i+1 = x_i, y_i+1 = y_i-1,

_i+1 = (x_i+1 + 1)² + (y_i+1 - 1)² – R ² = (x_i + 1)² + y²_i+1 - 2y_i+1 + 1 -R²=

= (x_i + 1)² + (y_i - 1)² – R ² - 2y_i+1 + 1 = _i - 2y_i+1 + 1.

Тепер ми можемо розглянути алгоритм Брезенхема побудови частини кола у першому квадрантi.

Програма, що реалiзує алгоритм Брезенхема креслення частини кола у першому квадрантi.

{Метод Брезенхема побудови частини кола у першому квадрантi}

unit Unit1;

interface {Unit1}

uses Windows, Messages, SysUtils, Classes, Graphics,

Controls, Forms, Dialogs, StdCtrls;

type TForm1 = class(TForm)

Label1,Label2,Label3:TLabel;Button1:TButton;

Edit1,Edit2,Edit3:TEdit;

procedure Button1Click(Sender: TObject);

private { Private declarations }

public { Public declarations }

end;

var Form1: TForm1;

implementation {Unit1}

{$R *.DFM}

var Xs,Ys,R : integer;

procedure RastrBresCircle(Xc,Yc,R,Color:integer);

var i,D,DL,DLP,Lim,x,y:integer;

{тут D=Dgreat,DL=DLitle,DLP=DLitlePrim}

begin {RastrBresCircle}

if R>0

then begin {R>0}

{початкове установлення змiнних}

x:=0;y:=R;

D:=2*(1-R);Lim:=0;

repeat {Початок головного циклу}

Form1.Canvas.Pixels[Xc+x,Yc+y]:=Color;

if y<=Lim then break;

if D<0

then begin {D<0}

DL:=2*D+2*y-1;

if DL<=0

then begin x:=x+1; D:=D+2*x+1; end

else begin x:=x+1;y:=y-1;D:=D+2*x-2*y+2; end;

end {D<0}

else begin {D>=0}

if D>0

then begin {D>0 }

DLP:=2*D-2*x-1;

if DLP<=0

then begin

x:=x+1;y:=y-1;

D:=D+2*x-2*y+2;

end

else begin

y:=y-1;

D:=D-2*y+1;

end;

end {D>0}

else begin {D=0}

x:=x+1;y:=y-1;D:=D-2*y+2;

end; {D=0}

end; {D>=0}

until false;

end; {R>0}

end;{RastrBresCircle}

procedure TForm1.Button1Click(Sender: TObject);

begin {TForm1.Button1Click}

Xs:=StrToInt(Edit1.Text);

Ys:=StrToInt(Edit2.Text);

R:=StrToInt(Edit3.Text);

RastrBresCircle(Xs,Ys,R,clGreen);

end; {TForm1.Button1Click}

end. {Unit1}

Лiтература. [22], [5]