
- •К.А.Джафаров Теория вероятностей и Математическая Статистика
- •Общие сведения
- •2. Рабочая программа оглавление
- •Общая характеристика направления
- •521600 Экономика
- •2.Требования к основной образовательной программе подготовки бакалавра по направлению 521600 «экономика»
- •3.Требования к обязательному минимуму содержания основной образовательной программы подготовки бакалавра по направлению 521600 «экономика»(раздел общие математические дисциплины)
- •Теория вероятностей и математическая статистика
- •II. Цели и задачи дисциплины.
- •III. Принципы построения курса
- •IV. Структура и содержание курса Лекции – 68 часов Практические занятия – 51 час
- •Модуль 1. Случайные величины и их вероятности
- •Модуль 4. Цепи Маркова
- •Модуль 6. Оценивание неизвестных параметров
- •Модуль 7. Проверка статистических гипотез
- •III семестр (34 часа)
- •1. Случайные величины и их вероятности (12 часов)
- •IV cеместр (34 часа)
- •4. Цепи Маркова (6 часов)
- •5. Основные понятия математической статистики (4 часа)
- •6. Оценивание неизвестных параметров (8 часов)
- •7. Проверка статистических гипотез (8 часов)
- •8. Примеры статистических методов обработки данных (8 часов)
- •V. Деятельность студентов. Практические занятия
- •III семестр (17 часов)
- •1. Случайные величины и их вероятности (6 часов)
- •IV cеместр (34 часа)
- •4. Цепи Маркова (6 часов)
- •5. Основные понятия математической статистики (4 часа)
- •6. Оценивание неизвестных параметров (8 часов)
- •7. Проверка статистических гипотез (8 часов)
- •8. Примеры статистических методов обработки данных (8 часов)
- •Контрольные мероприятия
- •VI. Самостоятельная работа студента
- •Литература
- •Дополнительная литература
- •Приложение. Вариант контрольной работы № 1
- •Вариант контрольной работы № 2
- •Глава 1 события и их вероятности
- •1.1. Аксиомы теории вероятностей. Вероятностные пространства
- •Случайные события. Операции над ними
- •1.1.2. Вероятности
- •1.1.3. Свойства вероятностей
- •Задачи к 1.1
- •1.2. Схема равновозможных исходов
- •1.2.1. Элементы комбинаторики
- •1.2.2. Классическая вероятность
- •1.2.3. Геометрическая вероятность
- •1.2.4. Гипергеометрическое распределение
- •Задачи к 1.2
- •Условные вероятности. Формула полной вероятности. Формулы Байеса
- •1.3.1. Условные вероятности
- •1.3.2. Формула полной вероятности
- •1.3.3. Формулы Байеса
- •Задачи к 1.3
- •1.4. Независимость случайных событий
- •1.4.1. Независимость двух событий
- •1.4.2. Независимость нескольких событий
- •Задачи к 1.4
- •1.5. Дополнительные задачи к Главе 1
- •Глава 2 случайные величины и их распределения
- •2.1. Случайные величины со значениями в 1
- •2.1.1. Случайные величины
- •2.1.2. Функция распределения
- •2.1.3. Свойства функции распределения
- •Задачи к 2.1
- •2.2. Дискретный и непрерывный типы распределений
- •2.2.1. Дискретная случайная величина
- •2.2.2. Непрерывная случайная величина
- •2.2.3. Примеры случайных величин
- •Задачи к 2.2
- •2.3. Функция от случайной величины
- •Задачи к 2.3
- •2.4. Случайные величины со значениями в n.
- •2.4.1. Случайные векторы
- •2.4.2. Дискретные и непрерывные двумерные случайные величины
- •2.4.3. Независимость случайных величин
- •Задачи к 2.4
2.3. Функция от случайной величины
Рассмотрим на вероятностном пространстве {, F, Р} случайную величину = (). Возьмем обычную числовую функцию (х), х 1. Сопоставляя каждому элементарному событию число () по формуле () = (()), мы получим новую случайную величину , которую и назовем функцией f от случайной величины .
Функция = () от дискретной случайной величины также является дискретной случайной величиной, поскольку она не может принимать больше значений, чем случайная величина . Если случайная величина имеет следующую таблицу распределения
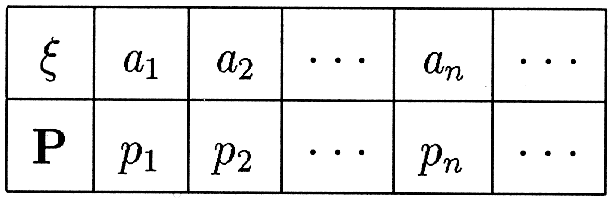
то таблица распределения случайной величины = () определяется так:

при этом, если появляются одинаковые значения (аi), то соответствующие столбцы надо объединить в один, приписав им суммарную вероятность.
Функция = () от непрерывной случайной величины может быть как непрерывной, так и дискретной (дискретной в том случае, когда множество значений f(x) — не более чем счетное).
Т![]() еперь
найдем функцию распределения
= ()
по заданной плотности p(t).
По определению
F(x)
= Р(
< x)
= Р((())
< x).
Последнюю вероятность можно определить,
используя аксиому «сложения» вероятностей,
просуммировав вероятности всех возможных
значений t
случайной величины ,
для которых (t)
< х. Заменяя
сумму на интеграл, получаем
еперь
найдем функцию распределения
= ()
по заданной плотности p(t).
По определению
F(x)
= Р(
< x)
= Р((())
< x).
Последнюю вероятность можно определить,
используя аксиому «сложения» вероятностей,
просуммировав вероятности всех возможных
значений t
случайной величины ,
для которых (t)
< х. Заменяя
сумму на интеграл, получаем
Задачу нахождения распределения можно упростить в некоторых случаях.
1![]() ).
Пусть (x)
—монотонно возрастающая функция. В
этом случае событие {f
(())
< х}
совпадает с событием {()
< f -1(x)},
где f -1
обратная к f
функция, и,
следовательно,
).
Пусть (x)
—монотонно возрастающая функция. В
этом случае событие {f
(())
< х}
совпадает с событием {()
< f -1(x)},
где f -1
обратная к f
функция, и,
следовательно,
2![]() ).
Пусть, кроме того,
— непрерывная случайная величина, а f
-1
имеет производную (f
-1(x)).
Тогда случайная величина
также является непрерывной, и ее плотность
распределения определяется с помощью
дифференцирования сложной функции
).
Пусть, кроме того,
— непрерывная случайная величина, а f
-1
имеет производную (f
-1(x)).
Тогда случайная величина
также является непрерывной, и ее плотность
распределения определяется с помощью
дифференцирования сложной функции
Пример 1. Пусть случайная величина распределена по нормальному закону с параметрами а и 2. Найдем распределение случайной величины = е. Здесь f(x) = eх, и f -1(x) = ln x. Пользуясь вышеуказанными рассуждениями получаем, что
![]()
Отметим, что полученное распределение случайной величины носит название логнормалъного.
П![]() ример
2. Пусть
— случайная величина, распределенная
по нормальному закону с параметрами а
и 2.
Найдем распределение случайной величины
=(
- а)/ .
Перепишем
ример
2. Пусть
— случайная величина, распределенная
по нормальному закону с параметрами а
и 2.
Найдем распределение случайной величины
=(
- а)/ .
Перепишем
тогда
-![]() плотность
стандартного нормального распределения.
плотность
стандартного нормального распределения.
Задачи к 2.3
1. Случайная величина подчинена распределению с плотностью
Н![]() айти
плотность p
(s), если
= A
+ В,
A
и В—постоянные.
айти
плотность p
(s), если
= A
+ В,
A
и В—постоянные.
2. Случайная
величина
![]() имеет показательное распределение с
параметром
имеет показательное распределение с
параметром
![]() = 2. Найти распределение случайной
.величины
= 2. Найти распределение случайной
.величины
![]() .
.
3. Случайная
величина
имеет плотность распределения
![]() Найти распределение случайной величины
Найти распределение случайной величины
![]()
2.4. Случайные величины со значениями в n.
2.4.1. Случайные векторы
Пусть {, F, Р} —вероятностное пространство, 1(),2(), …, n() — заданные на нем случайные величины. Для любого определим
()=(1(),2(), …, n()),
т.е. упорядоченную последовательность п случайных величин со значениями в 1.
Определение 1. Случайным вектором называется отображение
: n
Иногда, = (1, 2, … n) называется также многомерной случайной величиной. Здесь 1, 2, … n (проекции вектора на каждую ось) — случайные величины, заданные на одном и том же вероятностном пространстве {, F, Р }.
Определение 2. Функцией распределения случайного вектора называется следующая функция
F(x1, x2, …, xn)=P(1< x1, 2< x2, … , n< xn).
Функцию F(x1, x2, …, xn) называют также совместной функцией распределения случайных величин 1, 2, … n ..
В дальнейшем мы в основном будем иметь дело с двумерным случаем. Поэтому мы остановимся на нем, отметив, что n-мерный случай рассматривается аналогично.
Ограничимся перечислением свойств двумерной функции распределения, отметив лишь, что они доказываются аналогично соответствующим свойствам одномерной функции распределения.
1). 0 F(x1, x2) 1, для любых (x1, x2) 2.
2). F(x1, x2) — неубывающая функция по каждому из аргументов x1, x2.
3). F(-,
x2)
=
![]() F(
x1,
x2)
= 0, F(x1,
-)
=
F(
x1,
x2)
= 0, F(x1,
-)
=
![]() F(
x1,
x2)
= 0,
F(
x1,
x2)
= 0,
F(- , -) = F( x1, x2) = 0,
F(+
,
x2)
=
F(
x1,
x2)
= F![]() (x2),
(x2),
F(
x1,+)
=
F(
x1,
x2)
= F
![]() (x1),
(x1),
F( + ,+) = F( x1, x2) = 1.
4). P(a1 1< b1, a2 2< b2)= F( b1, b2)- F( b1, a2)- F( a1, b2)+ F( a1, a2).
5). F( x1, x2) — непрерывная слева по каждому из аргументов x1 и x2 функция.
