
- •«Национальный исследовательский ядерный университет «мифи»
- •«Элементы векторной алгебры и аналитической геометрии»
- •Умножение векторов
- •Переход к новому базису
- •Решение типовых задач
- •Решение. Объём пирамиды найдем, исходя из геометрического свойства
- •Элементы аналитической геометрии
- •Плоскость и прямая в пространстве Рассмотрим геометрические объекты, которые описываются линейными алгебраическими уравнениями.
- •Решение типовых задач
- •Прямая на плоскости
- •Взаимное расположение двух прямых на плоскости
- •Решение типовых задач
- •Решение типовых задач
Решение типовых задач
Пример.
Написать уравнение кривой, модуль
разности расстояний от каждой точки
которой до точек
![]() и
и
![]() равен 4.
равен 4.
Решение.
Пусть
![]() произвольная (текущая) точка искомой
кривой. Запишем аналитически (в виде
формулы) то свойство, которому должны
удовлетворять координаты любой точки
кривой. Найдем расстояние от точки
произвольная (текущая) точка искомой
кривой. Запишем аналитически (в виде
формулы) то свойство, которому должны
удовлетворять координаты любой точки
кривой. Найдем расстояние от точки
![]() до заданных точек
до заданных точек
![]() и
и
![]() :
:
![]() ;
;
![]() .
Согласно условию задачи
.
Согласно условию задачи
![]() или
или
![]() .
.
Упростим
это равенство, выполняя следующие
операции:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Окончательно
получим уравнение кривой
![]() ,
известное из школьного курса как
уравнение гиперболы, для которой оси
координат являются асимптотами.
,
известное из школьного курса как
уравнение гиперболы, для которой оси
координат являются асимптотами.
Пример.
Даны точка
![]() и прямая
и прямая
![]() .
В декартовых координатах составить
уравнение линии, каждая точка
которой:
.
В декартовых координатах составить
уравнение линии, каждая точка
которой:
а)
в
![]() раза ближе к точке
,
чем к данной прямой;
раза ближе к точке
,
чем к данной прямой;
б) в раза дальше от точки , чем от данной прямой;
в) равноудалена от точки и прямой .
Решение:
а) Пусть точка
![]() – основание перпендикуляра, опущенного
из точки
на прямую
.
Ее координаты
– основание перпендикуляра, опущенного
из точки
на прямую
.
Ее координаты
![]() .
Тогда согласно условия
.
Тогда согласно условия
![]() через координаты точек это равенство
запишется в виде
через координаты точек это равенство
запишется в виде
![]() .
.
Произведем упрощение полученного равенства:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
 .
.
Следовательно, искомая линия - эллипс. Точка совпадает с его правым фокусом, а прямая – правая директриса.
б)
Согласно условию задачи
![]() .
Следовательно,
.
Следовательно,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
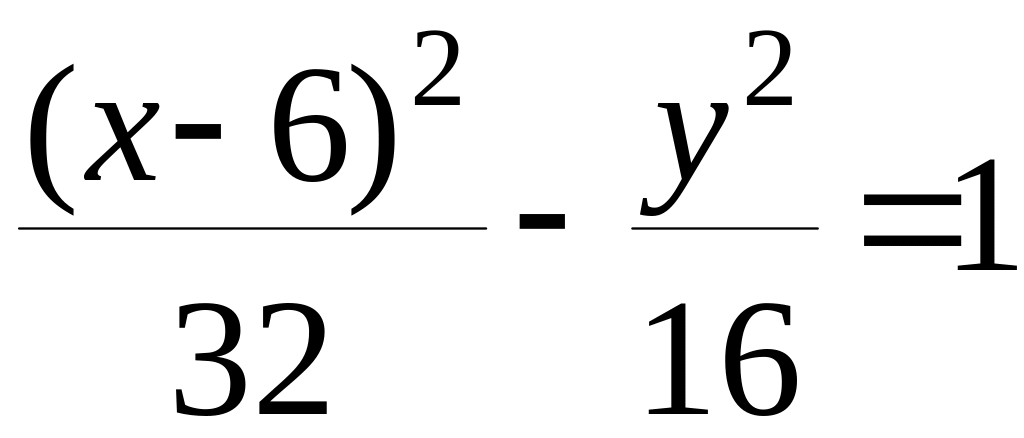 ,
,
т.е. данная линия – гипербола, для которой точка является левым фокусом, а прямая - левой директрисой.
в)
По условию
![]() .
Следовательно,
.
Следовательно,
![]() ;
;
![]() ,
,
![]() .
.
Получили уравнение параболы с фокусом в точке и директрисой .
Пример. Составить канонические уравнения:
а)
эллипса, расстояние между фокусами
которого
![]() ,
а точка
,
а точка
![]() лежит на кривой;
лежит на кривой;
б)
гиперболы с действительной полуосью
равной 8 и эксцентриситетом
 ;
;
в)
параболы, имеющей директрису
![]() .
.
Решение.
а) Каноническое уравнение эллипса имеет
вид
.
По условию задачи
![]() .
Для эллипса выполняется равенство
,
откуда
.
Для эллипса выполняется равенство
,
откуда
![]() .
Точка
лежит на кривой, поэтому должно выполняться
равенство
.
Точка
лежит на кривой, поэтому должно выполняться
равенство
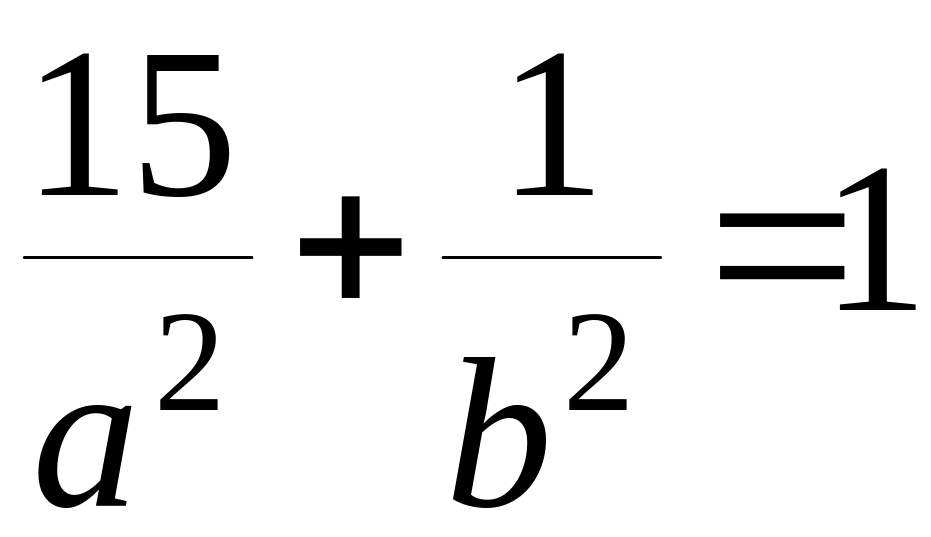 .
.
Значения
полуосей эллипса находим из системы
уравнений
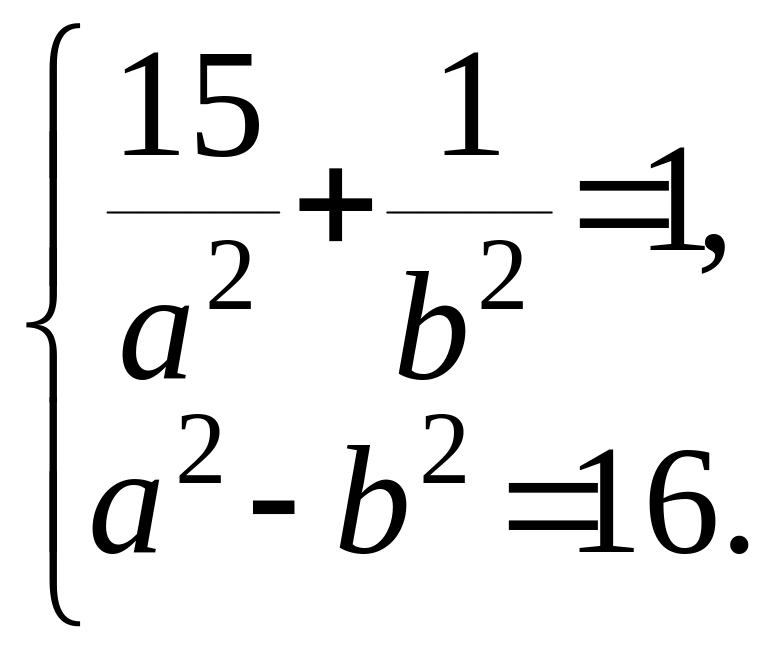 Эта система преобразуется
к виду
Эта система преобразуется
к виду

Из
первого уравнения имеем
![]() .
Исключим
.
Исключим
![]() из второго уравнения:
из второго уравнения:
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
Окончательно имеем
.
Окончательно имеем
 .
.
б)
Каноническое уравнение гиперболы имеет
вид
.
По условию действительная полуось
![]() .
Для гиперболы справедливо равенство
,
или
.
Для гиперболы справедливо равенство
,
или
![]() .
В свою очередь
.
В свою очередь
 .
Если учесть, что
,
то
.
Если учесть, что
,
то
![]() .
.
На
основании предыдущего равенства получим
![]() .
Искомое каноническое уравнение гиперболы
имеет вид
.
Искомое каноническое уравнение гиперболы
имеет вид
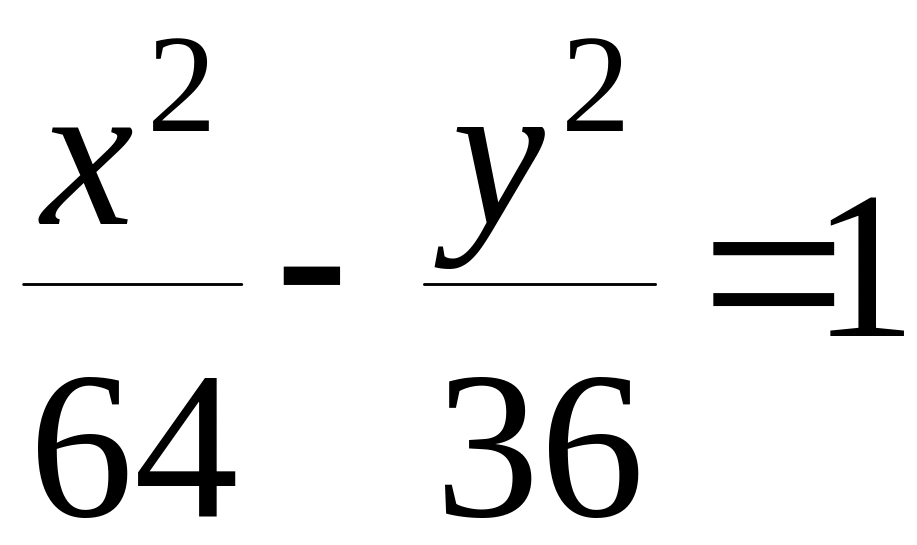 .
.
в)
В рассматриваемом случае каноническое
уравнение параболы должно иметь вид
,
а уравнение ее директрисы
.
Согласно условию уравнение директрисы
,
поэтому
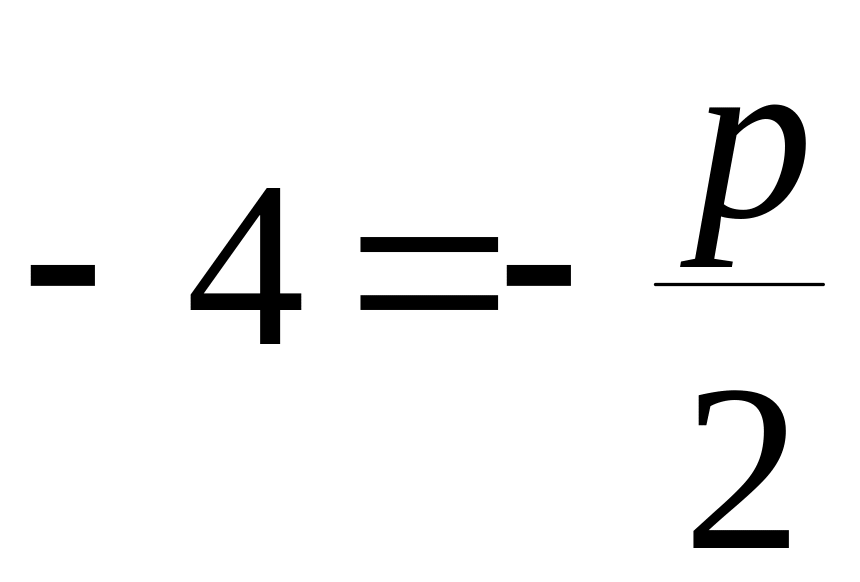 ,
откуда
,
откуда
![]() .
Искомое каноническое уравнение параболы
запишется в виде
.
Искомое каноническое уравнение параболы
запишется в виде
![]() .
.
