ВОПРОСЫ ПО ВЫСШЕЙ МАТЕМАТИКЕ НА СПЕЦИАЛЬНОСТИ

ХИМИЯ 1 КУРС, 2012 ГОД, ЛЕТО

1. Понятие первообразной. Свойства первообразных.

Определение. Функция F(х) называется первообразной для функции f(х) на заданном промежутке J, если для всех х из этого промежутка F`(х)= f(х). Так функция F(х)=х<sup>3</sup> первообразная для f(х)=3х<sup>2</sup> на (- ∞ ; ∞ ).  Так как, для всех х ~R справедливо равенство: F`(х)=(х³)`=3х²

Свойства первообразной

• Первообразная суммы равна сумме первообразных

• Первообразная произведения константы и функции равна произведению константы и первообразной функции

• Достаточным условием существования первообразной у заданной на отрезке функции f является непрерывность f на этом отрезке

У заданной на отрезке функции любые две первообразные отличаются на постоянную.

2. Понятие неопределенного интеграла. Свойства неопределенного интеграла.

Определение. Неопределенным интегралом ʃ f(x)dx называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е. ʃf(x)dx= F(x)+C или d(F(x)+C)=f(x)dx.

Таблица неопределенного интеграла(свойства):

1. ʃ +C; a≠-1

2. ʃ

3. ʃ cosx =sinx+C

4. ʃ sinx =-cosx+C

5. ʃ

6. ʃ

7. ʃ

8. ʃ

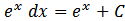
9. ʃ =arcsin x + C

10. ʃ = arcos x + C

3. Основные методы нахождения неопределенных интегралов.

1) По таблице неопределенных интегралов

1. ʃ +C; a≠-1

2. ʃ

3. ʃ cosx =sinx+C

4. ʃ sinx =-cosx+C

5. ʃ

6. ʃ

7. ʃ

8. ʃ

9. ʃ =arcsin x + C

10. ʃ = arcos x + C

2) Метод разложения

∫ ( f(x) +g(x) ) dx = ∫ f(x) dx + ∫ g(x) dx

∫ A f(x) dx = A g(x) dx

3)Метод замены

Замену старой переменной M подсказывает сама подынтегральная функция

Пример: ∫ dx ∫ +

4)Метод внесения под дифференциал

Полезен, например когда замена неочевидна

ПРИМЕРЫ:

а) ∫

б)

4. Формула интегрирования по частям и ее вывод.

↓ Справедливость формулы проверяется непосредственно дифференцированием

(левая часть)’ (правая часть)’

Равенство показано ↑.

Примеры:

1)

2)

Отметим, чтобы применить интегрирование по частям чаще всего приходится предварительно применить подходящим образом внесение под дифференциал. (смотри пример№2)

ʃ cosx dx= ʃ cosx d =cosx - ʃ ʃ ʃsin d ʃ =(cosx+sinx) ʃ cosx

ʃ cosx = (sinx+cosx)

5. Интегрирование рациональных выражений. Деление многочленов.

деление имеет смысл, если степень числителя > или = степени знаменателя.

2) =

Степень < степени

Разложить на множители первой степени и второй степени с отрицательным дискриминантом

=a ... ... ...

6. Интегрирование рациональных выражений. Разложение в сумму элементарных дробей.

Разложить рациональную функцию на Σ элементарных дробей:

...+ +...+

+...+ + +...+ +..

7. Интегрирование рациональных выражений. Интегрирование элементарных дробей.

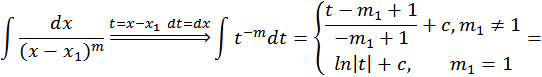
Если n=1

Если , проделывается с помощью интегрирования по частям

Подробнее:

1 этап: деление многочленов похоже на деление целых чисел:

можно использовать универсальный метод деления многочленов – деление уголком

2 этап: разложить знаменатель на множители 1-ой и 2-ой степени. Теория: любой множитель можно разложить на множители 1-ой и 2-ой степени с отрицательным дискриминантом.

Универсальных методов нахождения таких разложений нет. В примерах разложение можно угадывать.

3 Универсальный метод с помощью системы линейных уравнений. Для этого в правой части привести к общему знаменателю и приравнять коэффициенты при одинаковых степенях.

Пример:

Для решения СЛЧ известен метод: Выразить-подставить надежнее другой метод:

Функции равны, если равны числители (многочлены), а они равны только если коэффициенты равны