- •Понятие ф-и и способы ее задания
- •Функции в экономике
- •Вопрос 4. Числовая последовательность и ее пределы.
- •Вопрос 5. Предел функции, основные теоремы о пределах.
- •Вопрос 6. 1ый и 2ой замечательные пределы.
- •7.Бесконечно малые, бесконечно большие величины
- •8.Непрерывность функций. Точки разрыва, их классификация.
- •13. Производная и дифференциал высшего порядка.
- •14. Экономический смысл производной и понятие эластичности.
- •15. Приложение производной.
- •5.Теорема(правило) Лопиталя.
- •Вопрос 22 Экстремумы
- •Вопрос 23 Метод наименьших квадратов
- •24 Вопрос Неопределенный интеграл, свойства
- •25.Методы интегрирования неопред. Интеграла.
- •1. Непосредственное интегрирование.
- •2.Интегрирование по частям
- •3.Метод замены переменной
- •4.Интегрирование рациональных дробей.
- •27.Методы интегрирования определенноно интеграла.
- •28. Несобственные интегралы.
- •29. Дифференциальные уравнения.
- •30. Решение дифференциальных уравнений.
3.Метод замены переменной
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть
требуется вычислить интеграл ![]() Сделаем
подстановку
Сделаем
подстановку ![]() где
где ![]() —
функция, имеющая непрерывную производную.
—
функция, имеющая непрерывную производную.
Тогда ![]() и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
![]()
Замечание:
Новую переменную можно не вписывать явно. В этом случае говорят о преобразовании функции под знаком дифференциала, или о введении постоянных переменных под знак дифференциала.
4.Интегрирование рациональных дробей.
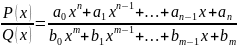
Дробь называется правильной, если n<m, в противном случае дробь наз-ся неправильной.
Пусть
![]() правильная дробь, тогда ее можно
представить в виде конечной суммы
элементарных дробей.
правильная дробь, тогда ее можно
представить в виде конечной суммы
элементарных дробей.
Можно выделить несколько типов рациональных дробей:
I.
Вид:![]() .
.
II.
Вид:![]() (k-целое
положительное число ³2).
(k-целое
положительное число ³2).
III.
Вид:![]() .
.
IY.
Вид:![]() (k-целое³2).
(k-целое³2).
Рассмотрим интегралы от простейших рациональных дробей.
I. ![]() .
.
II. ![]()
![]() =A
=A![]() .
.
III. ![]()
![]()
![]()
![]()
=![]()
=![]()
+![]() .
.
Более сложных вычислений требует интегрирование простейших дробей 4 типа.
IY.![]() .
.
26 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВ_ВА
![]()



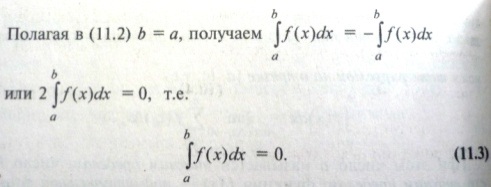
![]()
![]()




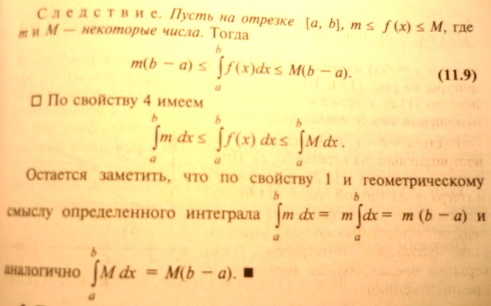

![]()


27.Методы интегрирования определенноно интеграла.
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующая формула:
![]() Предполагается,
что нахождение интеграла
Предполагается,
что нахождение интеграла ![]() проще,
чем
проще,
чем ![]() .
В противном случае применение метода
неоправдано.
.
В противном случае применение метода
неоправдано.
![]()
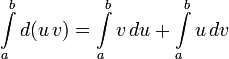
Все остальные методы интегрирования полностью переносятся на случай определенного интеграла(см. вопрос 25)
28. Несобственные интегралы.
Пусть
ф-я y=f(x)
интегрирована на отрезке [a,b],
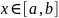 ,
то ф-я будет интегр. на
,
то ф-я будет интегр. на
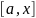 вложенном в
вложенном в
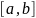 .
Тогда имеет место рав-во:
.
Тогда имеет место рав-во:
 .
.
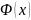 -интеграл
с переменным верхним пределом. Пусть
-интеграл
с переменным верхним пределом. Пусть
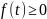 на [a,b],
тогда знач-е
-это
площадь под кривой
на [a,b],
тогда знач-е
-это
площадь под кривой
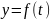 на
.
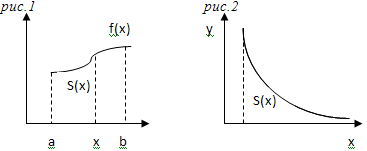
В этом состоит геом. смысл(рис.1). Можно
дать определ. для случая, когда
рассматривается интеграл с переменным
верхним пределом, причём верхний предел
определён несобственным числом. Тогда
имеет место особый вид интегр. –
несобственный интегр. Пусть
y=f(x)
интегрир. на отрезке [a,t],
т.е.
на
.
В этом состоит геом. смысл(рис.1). Можно
дать определ. для случая, когда
рассматривается интеграл с переменным
верхним пределом, причём верхний предел
определён несобственным числом. Тогда
имеет место особый вид интегр. –
несобственный интегр. Пусть
y=f(x)
интегрир. на отрезке [a,t],
т.е.
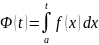 ,
,
 ,
тогда имеет место опр-е:
,
тогда имеет место опр-е:
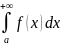 от ф-и f(x)
на полуинтервале
от ф-и f(x)
на полуинтервале
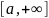 будем называть несобств. интегралом.
Для вычисления несобств. интегр. будем
пользоваться след. правилом:
будем называть несобств. интегралом.
Для вычисления несобств. интегр. будем
пользоваться след. правилом:
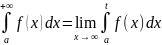 (1). Рассмотрим рав-во (1): если lim,
стоящий в правой части рав-ва (1) существует
и конечен, то несобств. интегр. называется
сходящимся к данному lim.
В противном случае интеграл расходящийся.
Аналогично определяется интегр. в
кот.нижний предел является числом
несобств., а именно:
(1). Рассмотрим рав-во (1): если lim,
стоящий в правой части рав-ва (1) существует
и конечен, то несобств. интегр. называется
сходящимся к данному lim.
В противном случае интеграл расходящийся.
Аналогично определяется интегр. в
кот.нижний предел является числом
несобств., а именно:
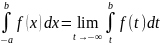 (2). Обобщая рав-ва (1) и (2) мы можем
сказать, что если y=f(x)
интегр. на [a,b],
то:
(2). Обобщая рав-ва (1) и (2) мы можем
сказать, что если y=f(x)
интегр. на [a,b],
то:
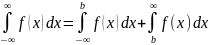 (3).(рис.2) S(x)=S
трапеции, ограниченной прямой x=a
и y=f(x)
на полуинтервале
и лучом y=0
на
.
Для того чтобы вычислить всю площадь
под кривой то:
(3).(рис.2) S(x)=S
трапеции, ограниченной прямой x=a
и y=f(x)
на полуинтервале
и лучом y=0
на
.
Для того чтобы вычислить всю площадь
под кривой то:
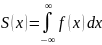 .
.