Линейная независимость

[править]

Материал из Википедии — свободной энциклопедии

В линейной алгебре линейная зависимость — это свойство, которое может иметь подмножество линейного пространства. Для этого должна существовать нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу. Если такой комбинации нет, то есть коэффициенты единственной такой линейной комбинации равны нулю,множество называется линейно независимым.

[Править]Пример

В   векторы  ,   и   линейно независимы, так как уравнение

имеет только одно, тривиальное, решение. Векторы   и   являются линейно зависимыми, так как

а значит

[Править]Определение

Пусть   будет линейное пространство над полем   и  .   называется линейно независимым множеством, если любое его конечное подмножество является линейно независимым.

Конечное множество   называется линейно независимым, если единственная линейная комбинация, равная нулю, тривиальна, то есть состоит из факторов, равных нулю:

Если существует такая линейная комбинация с минимум одним  ,   называется линейно зависимым. Обратите внимание, что в первом равенстве подразумевается  , а во втором  .

[Править]Свойства

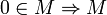•  линейно зависимо

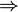•  линейно независимо     линейно независимо для всех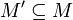 

•  линейно зависимо     линейно зависимо для всех 

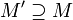
[Править]Значение

Линейные системы уравнений

Линейная система   уравнений, где   — количество переменных, имеет однозначное решение тогда и только тогда, когда столбцы её основной матрицы являются линейно независимыми.

Ранг матриц

Ранг матрицы равен числу её линейно независимых строк или столбцов.

Геометрический смысл

• Векторы 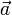  и   линейно зависимы тогда и только тогда, когда они коллинеарны (лежат на параллельных прямых).

• Векторы 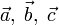  линейно зависимы тогда и только тогда, когда они компланарны (лежат в одной плоскости).

Базис

Базис линейного пространства является в частности множеством линейно независимых векторов.

Формула для вычисления корней n-й степени из любого ненулевого комплексного числа, представленного в тригонометрической форме, имеет следующий вид:                             

Подкольцо

[править]

Материал из Википедии — свободной энциклопедии

Подкольцо кольца   — это пара  , где   — кольцо, а   — мономорфизм (вложение) колец. Такое определение согласуется с общим понятием подобъекта втеории категорий.

В классическом определении подкольцо кольца   рассматривается как подмножество  , замкнутое относительно операций   и   из основного кольца. Это определение равносильно данному выше, однако в современном определении подчёркивается внутренняя структура подколец и связь между различными кольцами. Оно также легко обобщается на случай произвольных математических объектов (алгебраических, геометрических и т. п.). Разница между определениями аналогична разнице между теоретико-множественным и теоретико-категорным взглядом на математику.

В частности, различные определения кольца дают два основных содержательных понятия подкольца. В категории (всех) колец   подкольцо, как в классическом определении, можно рассматривать как произвольное подмножество кольца, замкнутое по сложению и умножению. Более интересная ситуация в категории колец с единицей  : морфизмы(гомоморфизмы)   в этой категории должны отображать единицу кольца   в единицу кольца   (аналогично гомоморфизму полугрупп с единицей), поэтому подкольцо  кольца   также обязано содержать единицу:  .

Категория   устроена гораздо лучше, чем  . Например, ядро любого гомоморфизма также является объектом этой категории. Из-за этого говоря о подкольце обычно подразумевают подкольцо в  , если не оговорено обратное.

Примеры

1. Любой идеал (левый, правый, двусторонний) замкнут относительно сложения и умножения, поэтому является подкольцом в  .

2. В   идеал является подкольцом только тогда, когда содержит 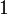 , поэтому он обязан совпадать со всем кольцом. Поэтому в   собственные идеалы не являются подкольцами.

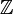3. В   подкольцами в   являются всевозможные главные идеалы 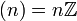 . В     не имеет собственных подколец.

4. Кольцо целых чисел   является подкольцом поля вещественных чисел 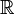  и подкольцом кольца многочленов 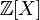 .