Логические операции

Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:

B = { Ложь, Истина }

Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.

Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты. Также вводятся дополнительные операции, такие как эквивалентность   («тогда и только тогда, когда»), импликация   («следовательно»), сложение по модулю два   («исключающее или»), штрих Шеффера  , стрелка Пирса  и другие.

Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция   приобретает смысл вычитания из единицы;   — немодульного сложения; & — умножения;   — равенства;   — в буквальном смысле сложения по модулю 2 (исключающее Или — XOR);   — непревосходства суммы над 1 (то есть A   B = (A + B) <= 1).

Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др.

[Править]Свойства логических операций

1. Коммутативность: x y = y x,  {&,  }.

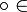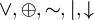2. Идемпотентность: x x = x,  {&,  }.

3. Ассоциативность: (x y) z = x (y z),  {&,  }.

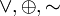4. Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:

   • ,

   • ,

   • .

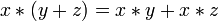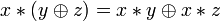5. Законы де Мо́ргана:

   • ,

   • .

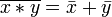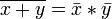6. Законы поглощения:

   • ,

   • .

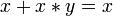7. Другие (1):

   • .

   • .

   • .

   • .

   • .

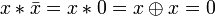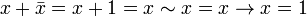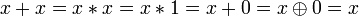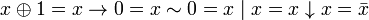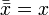8. Другие (2):

   • .

   • .

   • .

   • 

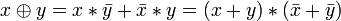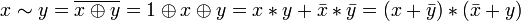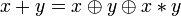
9. Другие (3) (Дополнение законов де Мо́ргана):

   • .

   • .

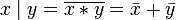Существуют методы упрощения логической функции: например, Карта Карно, метод Куайна - Мак-Класки

Билет №16

основные законы преобразования алгебры логики

В алгебре логики имеются законы, которые записываются в виде соотношений. Логические законы позволяют производить равносильные (эквивалентные) преобразования логических выражений. Преобразования называются равносильными, если истинные значения исходной и полученной после преобразования логической функции совпадают при любых значениях входящих в них логических переменных.

Для простоты записи приведем основные законы алгебры логики для двух логических переменных А и В. Эти законы распространяются и на другие логические переменные.

1. Закон противоречия:

2. Закон исключенного третьего:

3. Закон двойного отрицания:

4. Законы де Моргана:

5. Законы повторения: A & A = A; A v A = A; В & В = В; В v В = В.

6. Законы поглощения: A ? (A & B) = A; A & (A ? B) = A.

7. Законы исключения констант: A ? 1 = 1; A ? 0 = A; A & 1 = A; A & 0 = 0; B ? 1 = 1; B ? 0 = B; B & 1 = B; B & 0 = 0.

8. Законы склеивания:

9. Закон контрапозиции: (A ? B) = (B ? A).

Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных A, В и С:

1. Коммутативный закон: A & B = B & A; A ? B = B ? A.

2. Ассоциативный закон: A & (B & C) = (A & B) & C; A ? (B ? C) = (A ? B) ? C.

3. Дистрибутивный закон: A & (B ? C) = (A & B) ? (A & C).

Как уже отмечалось, с помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций: первыми выполняются операции в скобках, затем в следующем порядке: инверсия (отрицание), конъюнкция ( & ), дизъюнкция (v), импликация (?), эквиваленция (?)

Билет №17

построение таблиц истинности, логические законы

Порядок выполнения логических операций в сложном логическом выражении:

инверсия;

конъюнкция;

дизъюнкция;

импликация;

эквивалентность.

Для изменения указанного порядка выполнения операций используются скобки.

Алгоритм построения таблиц истинности для сложных выражений:

Определить количество строк:

количество строк = 2n + строка для заголовка,

n - количество простых высказываний.

Определить количество столбцов:

количество столбцов = количество переменных + количество логических операций;

определить количество переменных (простых выражений);

определить количество логических операций и последовательность их выполнения.

Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.

Таблица простейших логических функций:

 

Отрицание					Конъюнкция						Дизъюнкция				Следование					Эквивалентность
A	¬А			A		B	AB			A		B	AB		A	B	АВ				A	B	АВ
1	0			1		1	1			1		1	1		1	1	1				1	1	1
0	1			1		0	0			1		0	1		1	0	0				1	0	0
				0		1	0			0		1	1		0	1	1				0	1	0
				0		0	0			0		0	0		0	0	1				0	0	1

 

Законы логики и правила преобразования логических выражений

    В алгебре, которую мы изучаем в школе, существуют пять основных законов: переместительные, сочетательные и распределительный. Среди законов алгебры логики есть по­добные законы.

 

 

 

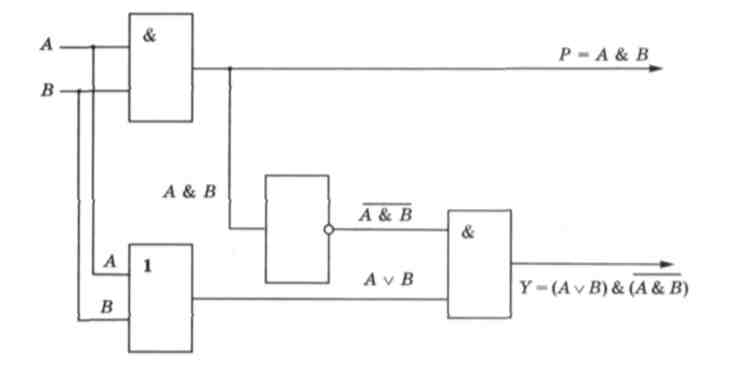
    C использованием законов алгебры логики выполняются преобразования сложных логических функций.

    Если логическая функция представлена с помощью дизъ­юнкций, конъюнкций и инверсий, то такая форма представ­ления называется нормальной.

    Логическая функция называется тождественно ложной, если она принимает значение «ложь» на всех наборах вхо­дящих в нее простых высказываний. Например:

В&¬А&(В  А) = В &¬А & (¬В A) = В & ((¬А & ¬В)  (¬А & А)) = В & (¬А & ¬В)  0 = (¬А & В &¬ В) = А & 0 = 0.

 

    Логическая формула называется тождественно истин­ной, если она принимает значение «истина» на всех наборах входящих в нее простых высказываний (тождественно ис­тинные высказывания часто называют тавтологиями). На­пример:

¬ (А&¬А)  (В ¬ В) = ¬0  1 = 1.