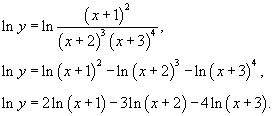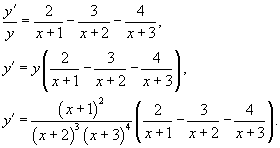Страница16

Функция. Способы задания функции.

Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.

Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.

Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.

Функция может быть определена разными формулами на разных участках области своего задания.

Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.

Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Пример 1: функция E(x) — целая часть числа x. Вообще через E(x) = [x] обозначают наибольшее из целых чисел, которое не превышает x. Иными словами, если x = r + q, где r — целое число (может быть и отрицательным) и q принадлежит интервалу [0; 1), то [x] = r. Функция E(x) = [x] постоянна на промежутке [r; r+1) и на нем [x] = r.

Пример 2: функция y = {x} — дробная часть числа. Точнее y ={x} = x - [x], где [x] — целая часть числа x. Эта функция определена для всех x. Если x — произвольное число, то представив его в виде x = r + q ( r = [x]), где r — целое число и q лежит в интервале [0; 1), получим {x} = r + q - r=q

Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитически.

Понятие предела функции.

В бытовом русском языке слово предел означает границу чего-либо. Напри-

мер, говорят: в пределах какой-то территории, в пределах какого-то промежутка вре-

мени, в пределах возможного.

Математический термин предел означает совсем другое. Для первоначального

представления можно так сказать …

Предел для переменной величины – это такое значение (число), к кото-

рому эта переменная величина в процессе своего изменения становится всѐ ближе и

ближе. Причѐм тут не важно, достигает или не достигает переменная величина этого

значения.

Непрерывность функции. Точки разрыва функции.

Непрерывность функции. Точки разрыва функции

Посвятим очередную статью одному из наиболее важных понятий математического анализа понятию непрерывность функции и точкам разрыва. Также приведем переченьосновных свойств непрерывных функций. Множество теорем и утверждений доказываются на основании непрерывных функций и их свойств. Непрерывные функции       Определение 1: Функция f(x) называется непрерывной функцией в точке A, если существует предел данной функции при аргументе стремящимся к A и он равен f(a), т.е.  .      Критерий непрерывности: Другими словами, для любого сколь угодно малого числа эпсилон, существует такое число дельта, зависящее от эпсилон, что из того, что для любых иксов удовлетворяющих неравенству следует, что отличия значений функции в данных точках будет сколь угодно мало.      Критерий непрерывности функции в точке:       Функция будет непрерывна в точке A тогда и только тогда, когда она будет непрерывна в точке A и справа и слева, т.е чтобы в точке A существовали два односторонних предела, они были равны между собой и равнялись значению функции в точке A.       Определение 2: Функция непрерывна на множестве, если она непрерывна во всех точках этого множества.   Свойства непрерывных функций. Точки разрыва функций a) Свойства непрерывных функций       1) Если функция непрерывна в точке A, то она ограничена в некоторой окрестности точки A. Данное свойство следует из локальной ограниченности функции, имеющей конечный предел.      2) Теорема о стабилизации знаков      Пусть функция непрерывна в точке A, причем f(A) отлично от нуля, тогда существует окрестность точки A такая, что знак функции в окрестности будет совпадать со знаком функции в точке A.      3) Пусть функции f и g непрерывны в точке A, тогда: n*f + m*g также будет непрерывной функцией в точке A, где n,m - константы. f*g, f/g (при g(A) отличном от нуля) будут непрерывными функциями   b) Точки разрыва функции     Определение 3: Точку В из области определения функции будем называть точкой разрыва функции, если функция не является непрерывной в точке B.  1) Точка разрыва функции называется точкой неопределенности, если не существует правого либо левого одностороннего предела.  2) Если существует оба односторонних предела, но по крайней мере один из них не конечен , то точка разрыва называется точкой бесконечного скачка  3) Если существует оба односторонних предела, но они не равны между собой , то точка разрыва называется точкой конечного скачка  4) Если существует оба односторонних предела и они не равны между собой, но не равны значению функции в данной точке, то точка разрыва называется точкой устраненного разрыва      Разрывы из пунктов 1) и 2) называются разрывами второго рода, а из пунктов 3) и 4)разрывами первого рода.

Понятие односторонних пределов. Основные теоремы о пределах.

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственнолевосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва).Определения Править

Пусть задана числовая функция   и   — предельная точка области определения M.

• Число   называется правосторонним пределом функции f при x стремящемся к a, если

• Число   называется левосторонним пределом функции f при x стремящемся к a, если

Обозначения Править

• Правосторонний предел принято обозначать любым из нижеследующих способов:

• Аналогичным образом для левосторонних пределов приняты обозначения:

Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.

   .

Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функцииg(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).

   .

Теорема 3. Предел постоянной равен самой постоянной.

.

Доказательство. f(x)=с,    докажем, что     .

Возьмем  произвольное >0. В качестве  можно взять любое

положительное число. Тогда при 

.

Теорема 4. Функция не может иметь двух различных пределов в

одной точке.

Доказательство. Предположим противное. Пусть

  и   .

По теореме о связи предела и бесконечно малой функции:

f(x)-A=  - б.м. при  ,

f(x)-B=  - б.м. при  .

Вычитая эти равенства, получим:

 B-A= - .

Переходя к пределам в обеих частях равенства при  , имеем:

B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.

Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при  , то и алгебраическая сумма имеет предел при  , причем предел алгебраической суммы равен алгебраической сумме пределов.

.

Доказательство. Пусть  ,   ,    .

Тогда, по теореме о связи предела и б.м. функции:

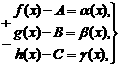 где   - б.м. при .

Сложим алгебраически эти  равенства:

f(x)+g(x)-h(x)-(А+В-С)= ,

где  б.м. при   .

По теореме о связи предела и б.м. функции:

А+В-С= .

Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при  , то и произведение имеет предел при , причем предел произведения равен произведению пределов.

.

Следствие. Постоянный множитель можно выносить за знак предела.

.

Теорема 7. Если функции f(x) и g(x) имеют предел при  ,

причем  , то и их частное имеет предел при  , причем предел частного равен частному пределов.

,   .

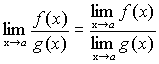Понятие бесконечно малые величин и бесконечно больших функций. Замечательные пределы.

Понятие бесконечно малых и бесконечно больших величин играет важную роль в математическом анализе. Многие задачи просто и легко решаются используя понятия бесконечно больших и малых величин.

Бесконечно малые.

Переменная   называется бесконечно малой, если для любого   существует такое значение   , что каждое следующии за ним значение   будет по абсолютной величине меньше   .

Если   - бесконечно малая то говорят, что   стремится к нулю, и пишут:   .

Бесконечно большие.

Переменная x называется бесконечно большой, если для всякого положительного числа cсуществует такое значение   , что каждое следующее за ним x будет по абсолютной величине больше   . Пишут: 

Величина, обратная к бесконечно большой, есть величина бесконечно малая, и обратно. 

Первый замечательный предел

Рассмотрим следующий предел:   (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).

Согласно нашему правилу нахождения пределов (см. статью Пределы. Примеры решений) пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида  , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:

 

Данный математический факт носит название Первого замечательного предела.

Нередко в практических  заданиях функции могут быть расположены по-другому, это ничего не меняет:

 – тот же самый первый замечательный предел.

! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде  , то и решать его нужно в таком же виде, ничего не переставляя.

На практике в качестве параметра   может выступать не только переменная  , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.

Примеры: ,  ,  , 

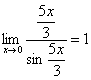Здесь  ,  ,  ,  , и всё гуд – первый замечательный предел применим.

А вот следующая запись – ересь:

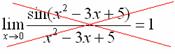
Почему? Потому-что многочлен   не стремится к нулю, он стремится к пятерке.

Кстати, вопрос на засыпку, а чему равен предел  ? Ответ можно найти в конце урока.

На практике не все так гладко, почти никогда студенту не предложат решить халявный предел   и получить лёгкий зачет. Хммм… Пишу эти строки и пришла в голову очень важная мысль – все-таки «халявные» математические определения и формулы вроде    лучше помнить наизусть, это может оказать неоценимую помощь на зачете, когда вопрос будет решаться между «двойкой» и «тройкой», и преподаватель решит задать студенту какой-нибудь простой вопрос или предложить решить простейший пример («а может он (а) все-таки знает чего?!»).

Переходим к рассмотрению практических примеров:

Пример 1

Найти предел 

Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.

Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):

Итак, у нас есть неопределенность вида  , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится  , а в знаменателе  .

В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас  , значит, в знаменателе нам тоже нужно получить  ».  А делается это очень просто:

То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания. Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:

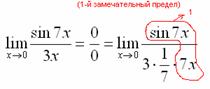Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении: 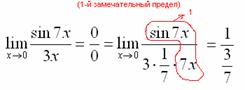Теперь только осталось избавиться от трехэтажности дроби: 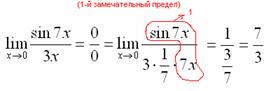Готово. Окончательный ответ: 

Если не хочется использовать пометки карандашом, то решение можно оформить так:

“ Используем первый замечательный предел  “

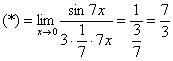Пример 2

Найти предел 

Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:

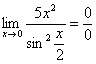
Действительно, у нас неопределенность   и, значит, нужно попытаться организовать первый замечательный предел. На уроке Пределы. Примеры решений мы рассматривали правило, что когда у нас есть неопределенность  , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):

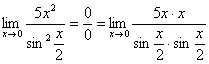
Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас  , значит, в числителе тоже нужно получить  :

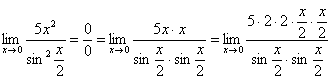
Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:

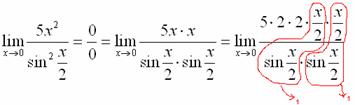
Собственно, ответ готов:

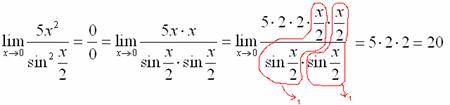
В следующих примерах, я не буду заниматься художествами в Пэйнте, думаю, как правильно оформлять решение в тетради – Вам уже понятно.

Второй замечательный предел

В теории математического анализа доказано, что:

Данный факт носит название второго замечательного предела.

Справка:   – это иррациональное число.

В качестве параметра   может выступать не только переменная  , но и сложная функция.Важно лишь, чтобы она стремилась к бесконечности.

Пример 6

Найти предел 

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение   , по какому принципу это делается, разобрано на уроке Пределы. Примеры решений.

Нетрудно заметить, что при   основание степени  , а показатель –  , то есть имеется, неопределенность вида  :

Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр  , значит, в показателе нам тоже нужно организовать   . Для этого возводим основание в степень  , и, чтобы выражение не изменилось – возводим в степень  :

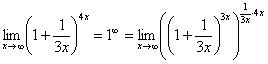
Когда задание оформляется от руки, карандашом помечаем:

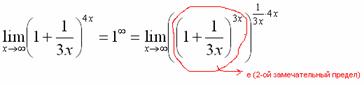Практически всё готово, страшная степень превратилась в симпатичную букву  :

При этом сам значок предела перемещаем в показатель.

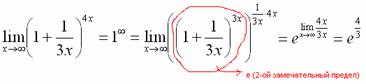
Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.

Пример 7

Найти предел 

Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.

Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:

В результате получена неопределенность  . Но второй замечательный предел применим к неопределенности вида  . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас  , значит, в числителе тоже нужно организовать  :

Теперь можно почленно разделить числитель на знаменатель:

Вроде бы основание стало напоминать  , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:

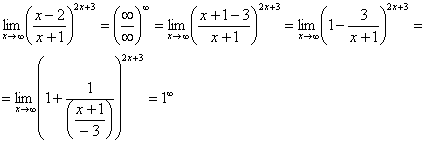
Таким образом, основание приняло вид  , и, более того, появилась нужная нам неопределенность  . Организуем второй замечательный предел  . Легко заметить, что в данном примере  . Снова исполняем наш искусственный прием: возводим основание степени в  , и, чтобы выражение не изменилось – возводим в обратную дробь  :

Наконец-то долгожданное   устроено, с чистой совестью превращаем его в букву  :

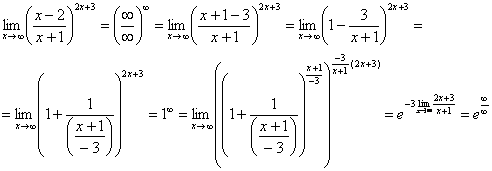
Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида  , раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на  :

Готово.

А сейчас мы рассмотрим модификацию второго замечательного предела. Напомню, что второй замечательный предел выглядит следующим образом:  . Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:

Производная функции, её механический и геометрический смысл

Производная. Рассмотрим некоторую функцию  y = f ( x ) в двух точках  x₀  и  x₀ +  :  f ( x₀ ) и  f ( x₀ +   ). Здесь через   обозначенонекоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции:  f ( x₀ +   )  f ( x₀ ) называется приращением функции. Производной функции  y = f ( x ) в точке  x₀  называется предел:

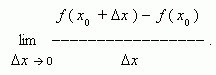
Если этот предел существует, то функция   f ( x )  называется дифференцируемой в точке  x₀ . Производная функции   f ( x ) обозначается так:

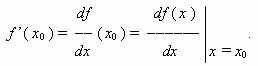
Геометрический смысл производной.  Рассмотрим график функции  y = f ( x ): 

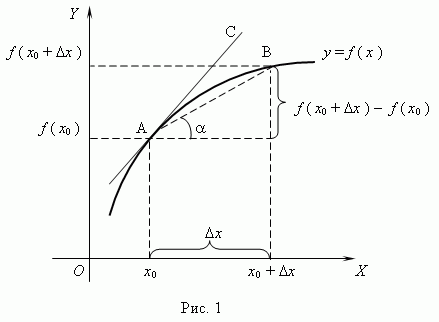
Из рис.1  видно, что для любых двух точек A и B графика функции:  

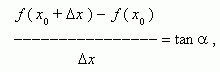
где    - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то    неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x₀ ,  f ( x₀  ) ). В общем случае уравнение прямой с угловым коэффициентом  f ’( x₀ )  имеет вид: 

y = f ’( x₀ ) · x + b .

Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:

f ( x₀ ) = f ’( x₀ ) · x₀ + b ,

отсюда,  b =  f ( x₀ ) – f ’( x₀ ) · x₀ , и подставляя это выражение вместо  b, мы получим  уравнение касательной:

y =  f ( x₀ ) +  f ’( x₀ ) · ( x – x₀  ) .

Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до t₀ +    точка перемещается на расстояние:  x ( t₀ +   )  x ( t₀ ) =  , а её средняя скорость равна:  v_a =    . При      0  значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смыслпроизводной. Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).

Производная суммы, разности, произведения и частного. Производная сложной и обратной функции.

Пусть теперь задана сложная функция  , т.е. переменная   есть функция переменной  , а переменная   есть, в свою очередь, функция от независимой переменной  .

Теорема. Если   и    дифференцируемые функции своих аргументов, то сложная функция   является дифференцируемой функцией и ее производная равна произведению производной данной функции по промежуточному аргументу и производной промежуточного аргумента  по независимой переменной:

.

Утверждение легко получается из очевидного равенства   (справедливого при   и  ) предельным переходом при   (что в силу непрерывности дифференцируемой функции влечет  ).

Перейдем к рассмотрению производной обратной функции.

Пусть на множестве   дифференцируемая функция    имеет множество значений   и на множестве   существует обратная функция .

Теорема. Если в точке   производная  , то производная обратной функции   в точке   существует и равна обратной величине производной данной функции:  , или

.

Эта формула легко получается из геометрических соображений.

Т ак как   есть тангенс угла наклона касательной линии   к оси  , то   есть тангенс угла наклона той же касательной (той же линии  ) в той же точке   к оси  . 

Если   и   острые, то 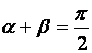 , а если тупые, то  .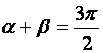

В обоих случаях 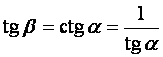 . Этому равенству и равносильно равенство

.

 

Дифференцирование неявных и параметрических функций. Логарифмическое дифференцирование.

21.1. Неявно заданная функция

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2^у-х+у=0).

Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

<< Пример 21.1

Найти производную функции у, заданную уравнением х³+у³-3ху=0.

Решение: Функция у задана неявно. Дифференцируем по х равенство х³+у³-3ху=0. Из полученного соотношения

3х²+3у² у'-3(1 у+х у')=0

следует, что у²у'-ху'=у-х², т. е. у'=(у-х²)/(у²-х).

21.2. Функция, заданная параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.

Найдем производную у'_х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'_х=y'_t•t'_x. С учетом равенства (21.2) получаем

Полученная формула позволяет находить производную у'_х от функции заданной параметрически, не находя непосредственной зависимости у от х.

<< Пример 21.2

Пусть  

Найти у'_х.

Решение: Имеем   x'_t=3t²,   y'_t=2t.   Следовательно,   у'_х=2t/t²,   т. е. 

В этом можно убедиться, найдя непосредственно зависимость у от х.

Действительно,    Тогда    Отсюда  т. е.

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.  Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей: Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x. Отсюда видно, что искомая производная равна

Пример 1

Вычислить производную функции  . Решение. Применяем логарифмическое дифференцирование:

Пример 2

Найти производную функции  . Решение. Прологарифмируем обе части и затем продифференцируем.

Пример 3

Вычислить производную функции  . Решение. Возьмем логарифм от обеих частей:        Теперь продифференцируем левую и правую части:

Производные высших порядков. Механический смысл производных высших порядков.

Пусть функция y=f(x) дифференцируема на некотором отрезке [a; b]. Значение производной f'(x), вообще говоря, зависит от x, т.е. производная f'(x) представляет собой тоже функцию переменной x. Пусть эта функция также имеет производную. Дифференцируя ее, получим так называемую вторую производную от функции f(x).

Производная от первой производной называется производной второго порядка или второй производной от данной функции y=f(x) и обозначается y''или f''(x). Итак, y'' = (y')'.

Например, если

у = х⁵, то y'= 5x⁴, а y''= 20x⁴.

Аналогично, в свою очередь, производную второго порядка тоже можно дифференцировать. Производная от второй производной называется производной третьего порядка или третьей производной и обозначается y'''или f'''(x).

Вообще, производной n-го порядка от функции f(x) называется производная (первая) от производной (n - 1)-го порядка и обозначается символом y⁽ⁿ⁾ или f⁽ⁿ⁾(x): y⁽ⁿ⁾ = (y^(n-1))'.

Таким образом, для нахождения производной высшего порядка от данной функции последовательно находят все ее производные низших порядков.

Примеры.

1. Найти производную четвертого порядка функции y= ln x.

.

.

2. Найти производную n-го порядка функции y = e^kx.

y'= k·e^kx, y''= k²·e^kx, y''' = k³·e^kx, …,y⁽ⁿ⁾ =kⁿ·e^kx.

3. Найти производную n-го порядка функции y = sin x.

Имеем

Выясним механический смысл второй производной. (Механический смысл первой производной - скорость).

Пусть материальная точка движется прямолинейно по закону s=s(t), где s - путь, проходимый точкой за время t. Тогда скорость vэтого движения есть v= s'(t) = v(t), т.е. тоже некоторая функция времени.

В момент времени t скорость имеет значение v=v(t). Рассмотрим другой момент времени t+Дt. Ему соответствует значение скорости v₁ = v(t+Дt). Следовательно, приращению времени Дt соответствует приращение скорости

Дv= v₁ - v = v(t + Дt) - v(t).

Отношение называется средним ускорением за промежуток времени Дt.

Ускорением в данный момент времени t называется предел среднего ускорения при Дt>0:

.

Таким образом, ускорение прямолинейного движения точки есть производная скорости по времени. Но как мы уже видели, скорость есть производная пути s по времени t: v = s'. Учитывая это, имеем:

a = v'(t) = (s')' = s''(t),

т.е. ускорение прямолинейного движения точки равно 2-й производной пути по времени

a = S''(t).

Дифференциал функции. Основные теоремы о дифференциалах. Применение дифференциала в приближенных вычислениях.

Итак, график дифференцируемой функции в окрестности каждой своей точки сколь угодно близко приближается к графику касательной в силу равенства:  где α – бесконечно малая в окрестности   функция. Для приближенного вычисления значения функции f в точке x₀ + Δx эту бесконечно малую функцию можно отбросить: 

Линейную функцию   называют дифференциалом функции f в точке   и обозначают df. Для функции x производная в каждой точке   равна 1, то есть   Поэтому пишут: 

Приближенное значение функции вблизи точки   равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом: 

Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.

Модель 3.3. Дифференциал функции
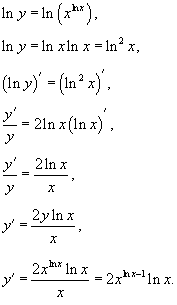
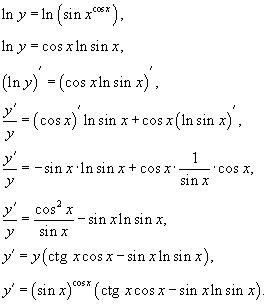
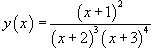