Кинетическая энергия при плоском движении.

Кинетическая энергия твердого тела представляет собой сумму кинетических энергий отдельных частиц:

где   - скорость центра масс тела,   - скорость i-й частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим:

так как   (суммарный импульс частиц в системе центра масс равен нулю).

Таким образом, кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений (теорема Кенига). Если рассматривать плоское движение как вращение вокруг мгновенной оси, то кинетическая энергия тела есть энергия вращательного движения.

2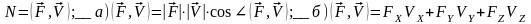 7)Элементарная работа сил. А=(F,dr) В общем случае слева стоит вариация полной работы.Силы:Активные – которые способны создать движение материальной точки.Пассивные – которые могут лишь изменить направление движения точки, но не могут его создать.Мощность силы – скалярное произведение двух векторов (F x V – в точке приложения силы).

Мощность пары сил – это скалярное произведение вектора момента пары и угловой скорости тела, к которому приложена пара сил.

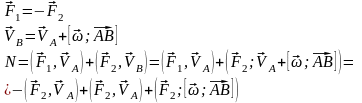
Из математики известно, что смешанное произведение может быть представлено в виде определителя.

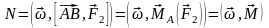
28)

Классификация связей.

Геометрические Кинематические

Удерживающие и неудерживающие Голономные и неголономные

Односторонние и двусторонние

Стационарные и нестационарные

Если какая –либо связь (геометрическая) может быть представлена в виде уравнения то связь называется удерживающей.

Е сли связь описывается неравенством – связь неудерживающая.

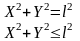
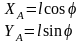
Стационарная связь – связь, уравнение которой явно не зависит от времени.

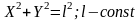
Нестационарная связь – связь, уравнение которой зависит от времени.

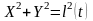
Голономные связи – связи, уравнения которых можно проинтегрировать

Неголономные связи – связи, уравнения которых невозможно проинтегрировать.

V _BX=0 V_AY=0

29)

Возможные и действительные перемещения.

Возможные перемещения – это такое бесконечно малое перемещение, которое имеет материальная точка в соответствии с наложенными на неё связями.

Возможная скорость – это такая скорость материальной точки, которую допускает наложенная на неё связь.

Д ействительное перемещение – это бесконечно малое перемещение, которое имеет материальная точка в соответствии с наложенными на неё связями, в зависимости от действия на неё сил.

Числом степеней свободы системы с голономными связями называют число обобщённых независимых координат, через которые можно выразить декартовы координаты всех точек системы.

30)

Идеальные связи.

Здесь рассматривается еще один вид связей, которые называются идеальными. Связь называется идеальной, если виртуальная работа ее реакции связи равна нулю:

Если на систему наложены только идеальные связи, то алгебраическая сумма виртуальных работ реакций связей на любых виртуальных перемещениях точек системы или виртуальная работа ее реакций связей равна нулю, то есть

Можно непосредственно убедиться в том, что эти условия выполняются для известных нам типов связей. Но при изучении теоремы об изменении кинетической энергии, где используется понятие элементарной работы, мы уже доказали, что элементарная работа реакций гладких поверхностей, идеальных шарниров равна нулю. Там же мы доказали, что равны нулю работа внутренних сил абсолютно твердых тел и реакций связей, всегда приложенных в мгновенном центре скоростей.

Следовательно, к идеальным связям относятся:

a) гладкие поверхности;

b) идеальные шарниры, где моменты сопротивления малы;

с) твердые тела - нерастяжимые стержни, нити и т.д.;

d) шероховатая твердая поверхность, по которой без скольжения катится твердое тело и т.д.

31)

Общее уравнение динамики (принцип Даламбера – Лагранжа)

Дана система из N материальных точек, имеющие произвольные, двусторонние неудерживающие связи. Согласно принципу Даламбера 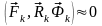. Но к системе сил, удовлетворяющей условиям равновесия, можно применить и условие равновесия, выражающееся принципом возможных перемещений Лагранжа: Сумма элементарных работ всех непосредственно приложенных к точкам системы активных сил, сил реакций связей и сил инерции равна 0 на любых возможных перемещениях системы из положений, занимаемых системой в текущий момент времени. Это можно выразить в виде уравнения:

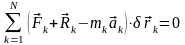
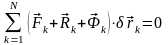Это уравнение представляет собой первую форму общего уравнения динамики. Заменяя силы инерции их выражениями 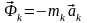и подставляя в полученное уравнение, получим или И наконец уравнение динамики можно представить в аналитической форме, выражая все скалярные произведения векторов через их проекции на декартовы оси.

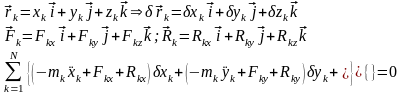
Последнее представление есть общее уравнение динамики в аналитическом виде.

Допустим, что связи, наложенные на систему, идеальны. Это значит, что сумма элементарных работ сил реакцией связей, тождественна, равна 0 на любом возможном перемещении системы из того или иного её положения, занимаемого в процессе движения. В этом случае сложится следующая ситуация:

32)

Е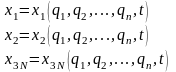 сть некоторая система N точек, на которые наложены голономные связи, выражающиеся несколькими ι уравнениями вида: _v(x_k, y_k, z_k,t)=0, (v=1, 2,…,ι). Таким образом, все 3N координат точек системы связаны между собой этими уравнениями. Эти ι уравнений, можно решить относительно каких то переменных, число которых равно ι, таким образом число независимых координат равно n=3N-ι. Перейдём от n независимых декартовых координат к каким то n зависимым обобщённым координатам, т. е. выразим независимые декартовые координаты через n независимых обобщённых координат q_i.

Числом степеней свободы системы с голономными связями называют число обобщённых независимых координат, через которые можно выразить декартовы координаты всех точек системы.

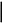
Если, как мы уже выяснили, через обобщённые координаты можно выразить декартовы координаты любой точки системы, следовательно, через обобщённые координаты можно выразить и радиус вектор этой точки: 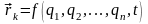. Для вычисления вектора r_k его можно рассматривать как полный дифференциал от , тогда полный дифференциал

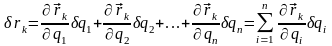
но 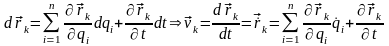Под вектором понимают вектор

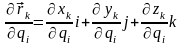
Обобщённые силы. Для формулировки этого понятия составим выражение сумм элементарных работ всех активных сил, приложенных к точкам системы.

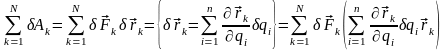Меняем порядок суммирования:

Обозначим внутреннюю сумму тогда равенство примет вид

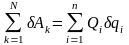
Выражение Q_i в координатной форме:

Величину Q_i называют обобщённой силой, соответствующей обобщённой координате q_i.

33) ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ В ОБОБЩЕННЫХ КООРДИНАТАХ

Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы обобщенные силы по каждой из обобщенных координат были равны 0.

Q1=0, Q2=0,……..Qs=0.

34)

Тождества Лагранжа.

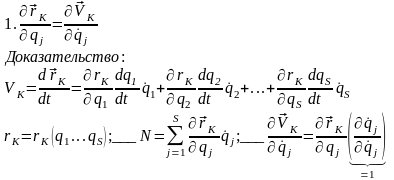
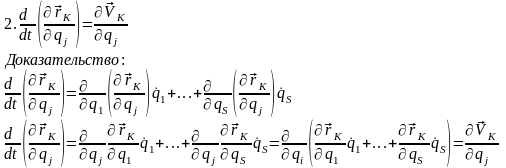
35) Д’Аламбера принцип — в механике: один из основных принципов динамики, согласно которому, если к заданным (активным) силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится уравновешенная система сил.

Назван по имени французского учёного Жана Д’Аламбера. Из данного приниципа следует, что для каждой i-той точки системы F_i + N_i + J_i = 0, где F_i — действующая на эту точку активная сила, N_i — реакция наложенной на точку связи, J_i — сила инерции, численно равная произведению массы m_i точки на её ускорение w_i и направленная противоположно этому ускорению (J_i = -m_iw_i,).

Принцип Д’Аламбера позволяет применить к решению задач динамики более простые методы статики, поэтому им широко пользуются в инженерной практике. Особенно удобно им пользоваться для определения реакций связей в случаях, когда закон происходящего движения известен или найден из решения соответствующих уравнений.

36)

Общее уравнение динамики (принцип Даламбера – Лагранжа)

Дана система из N материальных точек, имеющие произвольные, двусторонние неудерживающие связи. Согласно принципу Даламбера . Но к системе сил, удовлетворяющей условиям равновесия, можно применить и условие равновесия, выражающееся принципом возможных перемещений Лагранжа: Сумма элементарных работ всех непосредственно приложенных к точкам системы активных сил, сил реакций связей и сил инерции равна 0 на любых возможных перемещениях системы из положений, занимаемых системой в текущий момент времени. Это можно выразить в виде уравнения:

Это уравнение представляет собой первую форму общего уравнения динамики. Заменяя силы инерции их выражениями и подставляя в полученное уравнение, получим или И наконец уравнение динамики можно представить в аналитической форме, выражая все скалярные произведения векторов через их проекции на декартовы оси.

Последнее представление есть общее уравнение динамики в аналитическом виде.

37)

Аналогичным  образом в обобщенных координатах можно  записать и общее уравнение  динамики.

      Для  этого  определим с  помощью  обобщенных сил суммы элементарных работ на вариациях обобщенных координат рассматриваемой системы  отдельно для  заданных  сил  и  для сил  инерции.

       

38)

Уравнения Лагранжа второго рода.