89. Если есть число u, равномерно распределённое на [0;1), то число х, равномерно распределённое на [a,b) можно получить так:

Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a, b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.е.

Обозначение: .

Математическое ожидание: .

Дисперсия: .

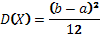Х, распределенная по равномерному закону на отрезке [0, 1] называется случайным числом от 0 до 1.

Если пользователю потребуется, чтобы случайное число x находилось в интервале (a; b), отличном от (0; 1), нужно воспользоваться формулой x = a + (b – a) · r, где r — случайное число из интервала (0; 1).

90. Если есть число u, равномерно распределённое на [0;1), то число х, равномерно распределённое на (a,b] можно получить так:

Тоже самое что и в 89

91. Если есть число u, равномерно распределённое на [0;1), то число х, соответствующее экспоненциальному закону распределения, можно получить с помощью выражения:

, где  - это и есть X, а R – просто случайная велечина

92. Если есть числа u, равномерно распределённые на [0;1), то число х, соответствующее нормальному закону распределения, можно получить с помощью выражения:

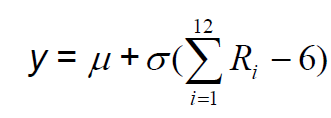, у=x.

Теория графов

93. Граф содержит:

• Рёбра, называется неориентированным; граф, содержащий только дуги, - ориентированным, или орграфом

94. Смежные вершины – это:

• соединенные ребром

95. Смежные рёбра – это:

• имеющие общую вершину

96. Пусть граф G содержит N вершин и M рёбер, тогда матрица смежности для графа будет иметь размерность:

• N*N

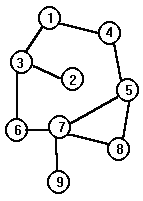97. Для графа на рисунке при обходе вершин поиском в глубину, начиная с третьей вершины, второй по счёту будет просмотрена вершина с номером:

• 1

98. Для графа на рисунке при обходе вершин поиском в глубину, начиная с третьей вершины, третьей по счёту будет просмотрена вершина с номером:

• 4

99. Для графа на рисунке при обходе вершин поиском в глубину, начиная с третьей вершины, четвёртой по счёту будет просмотрена вершина с номером:

• 5

100. Для графа на рисунке при обходе вершин поиском в глубину, начиная с третьей вершины, пятой по счёту будет просмотрена вершина с номером:

• 7

101. Для графа на рисунке при обходе вершин поиском в глубину, начиная с третьей вершины, шестой по счёту будет просмотрена вершина с номером:

• 6

102. Для графа на рисунке при обходе вершин поиском в глубину, начиная с третьей вершины, седьмой по счёту будет просмотрена вершина с номером:

• 8

103. Для графа на рисунке при обходе вершин поиском в глубину, начиная с третьей вершины, восьмой по счёту будет просмотрена вершина с номером:

• 9

104. Для графа на рисунке при обходе вершин поиском в глубину, начиная с третьей вершины, девятой по счёту будет просмотрена вершина с номером:

• 2

105. При нерекурсивной реализации алгоритма поиска в глубину наиболее удобно использовать для хранения номеров вершин:

• стек

106. Для графа на рисунке при обходе вершин поиском в ширину, начиная с третьей вершины, второй по счёту будет просмотрена вершина с номером:

• 1

107. Для графа на рисунке при обходе вершин поиском в ширину, начиная с третьей вершины, третьей по счёту будет просмотрена вершина с номером:

• 2

108. Для графа на рисунке при обходе вершин поиском в ширину, начиная с третьей вершины, четвёртой по счёту будет просмотрена вершина с номером:

• 6

109. Для графа на рисунке при обходе вершин поиском в ширину, начиная с третьей вершины, пятой по счёту будет просмотрена вершина с номером:

• 4

110. Для графа на рисунке при обходе вершин поиском в ширину, начиная с третьей вершины, шестой по счёту будет просмотрена вершина с номером:

• 7

111. Для графа на рисунке при обходе вершин поиском в ширину, начиная с третьей вершины, седьмой по счёту будет просмотрена вершина с номером:

• 5

112. Для графа на рисунке при обходе вершин поиском в ширину, начиная с третьей вершины, восьмой по счёту будет просмотрена вершина с номером:

• 8

113. Для графа на рисунке при обходе вершин поиском в ширину, начиная с третьей вершины, девятой по счёту будет просмотрена вершина с номером:

• 9

114. При реализации алгоритма поиска в ширину наиболее удобно использовать для хранения номеров вершин:

• очередь

115. Дерево в теории графов – это:

• произвольный связный неориентированный граф без циклов, содержащий N вершин и N-1 ребер, в котором каждая пара вершин соединена одной и только одной простой цепью.

116. Дерево в теории графов – это:

• произвольный связный неориентированный граф без циклов, содержащий N вершин и N-1 ребер, в котором каждая пара вершин соединена одной и только одной простой цепью.

117. На основе каких методов можно реализовать алгоритмы построения каркаса графа?

• На основе методов просмотра графа поиском в глубину и в ширину

118. Какие графы являются деревьями?

• связный неориентированный граф без циклов

119. Какие графы не являются деревьями?

• Несвязанный, циклический, блин, так сложно ответить…

120. Матрица достижимости:

• Для ориентированного графа G=(V,E), имеющего n вершин, матрицей достижимости называется квадратная матрица размерности n*n, в которой элемент xi,j = 1 тогда и только тогда, когда вершина хj достижима из вершины xi. В противном случае xi,j = 0

121. Матрица достижимости для связного неориентированного графа:

• Не уверен, но это матрица состоящая из одних 1-иц

122. Если некоторый элемент матрицы смежности A[i,j]=1, то элемент матрицы достижимости R[I,j]:

• 1

123. Граф может быть задан:

• Матрицей достижимостей

124. Метод Краскала

• Шаг 1. Начать с вполне несвязного графа G, содержащего N вершин.

Шаг 2. Упорядочить ребра графа G в порядке неубывания их весов.

Шаг 3. Начав с первого ребра в этом перечне, добавлять ребра в графе Q, соблюдая условие: добавление не должно приводить к появлению цикла в Q.

Шаг 4. Повторять шаг 3 до тех пор, пока число ребер в Q не станет равным N-1. Получившееся дерево является каркасом минимального веса.