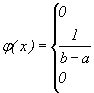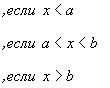[Править]Тождества
Из
свойств вероятности следует,
что 
,
таких что 
:
;
;
;
;
;
;
;
.
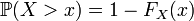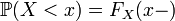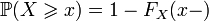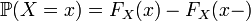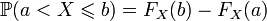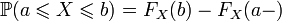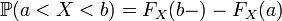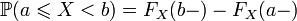24.плотность рапреления
Плотность распределения, плотность вероятности , плотность распределения вероятности в теории вероятностей — производная абсолютно непрерывной функции распределения.
Пусть ξ —
случайная величина с функцией
распределения F(x);
пусть существует неотрицательная
функция f(x) такая,
что для любых 
тогда 
называется плотностью
распределения случайной
величины ξ.
Для
любого борелевского множества 
Любая неотрицательная интегрируемая функция f(x), удовлетворяющая условию номировки
является плотностью распределения некоторой случайной величины ξ.
Плотность
многомерного распределения случайного
вектора 
определяется
как функция многих переменных 
такая,
что
где F — абсолютно непрерывная функция многомерного распределения случайного вектора ξ.
25.равномерное распределение
Равномерное
распределение.
Пусть
сегмент [a,b] оси Ox есть
шкала некоторого прибора. Допустим, что
вероятность попадания указателя в
некоторый отрезок шкалы пропорциональна
длине этого отрезка и не зависит от
места отрезка на шкале. Отметка указателя
прибора есть случайная величина 
могущая
принять любое значение из сегмента [a,b].
Поэтому 
.
Если, далее, x1 и x2 (x1<x2) -
две любые отметки на шкале, то согласно
условию имеем
где k - коэффициент пропорциональности, не зависящий от x1 и x2, а разность x2-x1, - длина сегмента[x1,x2]. Так как при x1=a и x2=b имеем , то k(b-a)=1, откуда k=1/(b-a). Таким образом
|
(26) |
Теперь
легко найти функцию F(x) распределения
вероятностей случайной величины
.
Если 
,
то 
так
как
не
принимает значений, меньших a.
Пусть теперь 
.
По аксиоме сложения вероятностей 
.
Согласно формуле (26), в которой
принимаемx1=a, x2=х имеем
Так
как 
,
то при
получаем
Наконец, если x>b, то F(x)=1, так как значения лежит на сегменте [a,b] и, следовательно, не превосходят b. Итак, приходим к следующей функции распределения:
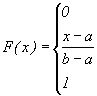
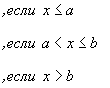
График
функции F(x) представлен на рис.
9.
Плотность
распределения вероятностей найдем по
формуле (25).
Если x<a или x>b,
то 
.
Если a<x<b,
то
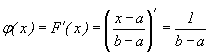
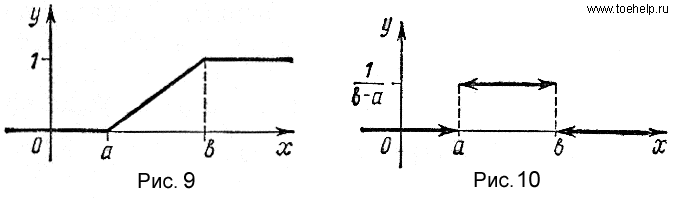
Таким образом,
|
(27) |
График
функции 
изображен
на рис. 10. Заметим, что в
точках a и b функция
терпит
разрыв.
Величина, плотность распределения которой задана формулой (27), называется равномерно распределенной случайной величиной.
26.нормальое распределение
Нормальное распределение, также называемое гауссовым распределением илираспределением Гаусса —распределение вероятностей, которое задается функцией плотности распределения:
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.
Нормальное распределение играет важнейшую роль во многих областях знаний, особенно встатистической физике. Физическая величина, подверженная влиянию значительного числа независимых факторов, способных вносить с равной погрешностью положительные и отрицательные отклонения, вне зависимости от природы этих случайных факторов, часто подчиняется нормальному распределению, поэтому из всех распределений в природе чаще всего встречается нормальное (отсюда и произошло одно из названий этого распределения вероятностей).
Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
27.показательное распределение