Теоретическая механика

Раздел №1 Движение свободных материальных точек

Тема №1 Кинематика точки

1. Основные понятия теоретической механики

Теоретическая механика изучает законы механического движения тел и механического взаимодействия, общие для любых материальных тел. Механическое движение – движение, выражающееся в изменении с течением времени взаимного положения тел или частей тела. Механическое взаимодействие – взаимодействие, вызывающее изменение механического движения. Чтобы рассмотреть общие свойства необходимо ввести абстрактные понятия:

1. Механическая точка – абстрактный образ материального тела, не имеющего размера, но обладающего массой.

2. Абсолютно твердое тело – это система материальных точек, расстояние между которыми не изменяется.

3. Сплошная среда – система с бесконечным числом степеней свободы.

4. Механическая система – мысленно выделенная по каким-либо признакам совокупность механических взаимодействий материальных точек или тел.

Один и тот же физический объект в зависимости от условий может быть и материальной точкой и твердым телом. В теоретической механике изучаю так же силы, которые действуют на точки и приводят их а движению.

2. Система отсчета, траектория, путь, перемещение.

При описании движения необходимо установить систему отсчета. Под СО в механике Ньютона понимают тело отсчета ( твердое тело, распространяющееся в пространстве точки, которую пронумеровали, то есть выделили систему координат) .положение материальной точки определяется радиус-вектором.. проведенного из начала координат в эту точку.

(1.1)

Изменение положения точки с течением времени определяется кинематическим законом движения:

(1.2)

где (1.2) параметрическое уравнение

пусть положение материальной точки в момент времени и , 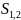– длина участка траектории между точками 1 и 2, который соответствует пройденному пути. Траектория – линия, которую описывает конец радиус-вектора, вектор, проведенный из 1 в 2 – перемещение . При криволинейном движении модуль перемещения меньше пройденного пути.

3. Скорость, ускорение точки. Разложение ускорения на нормальное и тангенциальное

Скорость – физическая величина, характеризующая быстроту изменения координаты со временем

Средняя скорость характеризует темп движения точки на участке 1 - 2, но не дает информации о быстроте движения точки. Если рассмотреть в пределе при величину средней скорости на участке , то получим мгновенную скорость, то есть скорость в данной точке или в данный момент времени: V(t)= (1.3)

Модуль вектора скорости характеризует быстроту движения точки, а направление указывает куда движется точка в данный момент времени.

= .

Продифференцируем по времени формулу 1.1 и получим следующее:

= (1.4)

Из 1.4 следует проекция скорости в декартовой системе координат:

(1.5)

Используя 1.5 определим модуль вектора, скорость и направление косинусов:

(1.6)

(1.7)

Зная закон движения можно, используя формулы 1.5 – 1.7 определить скорость точки.

Ускорение – физическая величина, которая характеризует быстроту изменения скорости. Если рассмотреть в пределе среднее ускорение на малом участке со скоростью получим мгновенное ускорение – ускорение в данный момент времени:

Если уравнение 1.1 дважды продифференцировать по времени то получим:

(1.9)

Из 1.9 следуют декартовые компоненты ускорения:

(1.10)

Используя 1.10 можно получить модуль ускорения и направляющие косинусы. Разложим ускорение на нормальное и тангенциальное. При движении точки ее скорость в общем случае меняется по модулю и направлению, это влияет на ускорение. Ускорение представляет собой сумму двух ускорений:

(1.11)

А иначе – сумму тангенциального и нормального ускорения. Тангенциальное ускорение является касательной к траектории, обусловливает только изменение модуля скорости, а нормальное ускорение обусловливает изменение направления скорости:

Нормальное ускорение получается при изучении и описании траектории малой дугой окружности. Окружность характеризуется радиусом кривизны, что дает криволинейную траекторию:

Тогда ускорение по модулю будет равно:

(1.12)

Направление соответствует направлению скорости в пределе, то есть перпендикулярна обычной скорости . Модуль полного ускорения:

Тангенциальное ускорение согласно 1.12 равно нулю, при равномерном движении существует нормальное ускорение. При неравномерном движении тангенциальное ускорение не равно нулю. При прямолинейном движении нормальное ускорение равно нулю. Полное ускорение равно нулю только при равномерном прямолинейном движении.

Если материальная точка движется по окружности, то кроме линейной кинетической величины используются угловые характеристики. – угол, описываемый радиус-вектором. Угловая скорость :

(1.13)

Угловое ускорение:

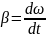(1.14)

Линейная скорость:

(1.15)

Линейное ускорение:

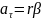(1.16)

Центростремительное ускорение:

(1.17)

Тема №2 Динамика материальной точки

4. Первый закон Ньютона. Преобразования Галилея

Согласно первому закону Ньютона система отсчета является инерциальной, относительно которой любая свободная материальная точка движется равномерно и прямолинейно.

Найдем все инерциальные системы отсчета и выясним, как в системе отсчета k связаны с радиус-векторами в системе отсчета k’, которая движется постоянно, равномерно, прямолинейно, относительно системы k.

В проекциях на декартовые оси

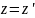(2.1)

(2.1) преобразование Галилея. Продифференцируем данное выражение по времени и учтем, что:

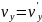
(2.2)

Продифференцировав (2.2) по времени получим соотношения для ускорения

(2.3)

Из формул (2.3) следует, что ускорение является одинаковым в обеих системах отсчета, то есть оно инвариантно относительно преобразования Галилея.

Движение материальной точки. Относительно системы отсчета k можно рассматривать как сумму двух движений:

1. Движение вместе с системой отсчета k’ , то есть движение с постоянной скоростью

2. Движение относительно системы k’

Пусть система отсчета k инерциальная, то есть . Согласно преобразованию Галилея (2.3) ускорение точки в системе k’ так же равно нулю. Если система k’ движется относительно kравномерно и прямолинейно, значит k’ – инерциальная система отсчета. Чтобы найти все инерциальные системы отсчета , достаточно найти одну, остальные будут инерциальные. Если движение относительно этой системы отсчета равномерное и прямолинейное, то инвариантом является так же и время.

5. Второй закон Ньютона как дифференциальное уравнение движения

Согласно первому закону Ньютона материальная точка, движущаяся с постоянной скоростью в инерциальной системе отсчета, является свободной и на нее не действуют другие тела. Воздействие со стороны приводит к изменению скорости, и возникает ускорение. В механике Ньютона воздействие тела друг на друга характеризуется векторной физической величиной , отсюда следует второй закон Ньютона – ускорение, приобретаемое материальной точкой относительно инерциальной системы отсчета пропорционально действию на нее результирующей силы. m – скалярная величина и при решении задач второй закон Ньютона записывается через скалярные величины, а затем в дифференциальной форме.

Где x, y, z – проекции равнодействующих сил в декартовой системе координат. В дифференциальном виде:

m

m

m

или можно переписать следующим образом:

(2.4)

У нас получилась система дифференциальных уравнений второго порядка. Решение данного уравнения позволяет определить кинематический закон движения точки, то есть решить основную задачу динамики материальной точки. Для однозначного определения траектории необходимо найти константы, которые задают начальные условия:

t=0, x(0)= , y(0)= , z(0)= , , ,

уравнения 2.4 уравнения движения свободной материальной точки в форме второго закона Ньютона.