6.Принцип относительности Галилея. Преобразования Галилея. З-ны физики не зависят от выбора инерциальн. Системы отсчёта. З-ны ньютона не завис от инерц со. V-скорость штриховой со , , . В случае, когда инерц. Со и тело движ-ся с малой скоростью, скор-ти склад-ся лин образом. Преобразования Галилея: , , . Векторная ф-ма: . С и тоже самое. Движение одной со относ другой должн быть равным и прямолин. 2ой з-н Ньютона инвареантен(НЕИЗМЕН ОТНОСИТ ПРЕОБР ГАЛИЛЕЯ) 3ий относ одной к другой со.

11. Теорема об изменении кинет энергии мех системы.

Под энергией системы понимают способность с-мы совершать работу. В механике 2 вида энергии: кинет и потен. Уравнение движения с-мы с помощью 2 закона Ньютона имеет вид

умножим скалярно на получим и

T=

Изменение кинет энергии мех с-мы обусловлено работой соверш над мех с-мой внутр и внеш силами, или мощностью сил. Для замкнутой с-мы

10.Теорема об изменении момента импульса механической системы

Умножим уравнение (3) и (4) векторно на [ -первую,а вторую[ в результате получаем уравнения

Где , -моменты импульса 1-ой и 2-ой материальной точки.

Сложим 2 этих уравнения (левые и правые части):

,где .

Т.о. соотношение (9) это и есть математическое выр-е теоремы об изменении момента импульса в мех. системе.Другими словами изменение момента импульса механ. сист в единицу времени равно сумме моментов внешних сил действующих на механ. сист..

Следствия:1)если внутренние силы явл-ся центральными,то

2)если механ. сист. явл-ся замкнутой,то в этом случае ,будет выполняться закон сохранения момента импульса для замкнутой механической системы или сумма момента импульса механической системы будет величина постоянная не зависящая от времени.

20. Метод неопределенных множителей Лагранжа

Суть метода заключается в том, что каждое тело хотя бы приближенно может быть представлено, как совокупность материальных точек, связанных определенными ограничениями. Для этой совокупности могут быть записаны стандартные уравнения механики, дополненные по методу Лагранжа условиями связей.

Коэффициенты при всех должны быть приравнены 0. Получаем, что между реакциями идеальных голономных связей и функциями , опред уравнения связей , имеют место соот-ния

32.Пусть мех.сис-ма опр-ся коор-ми q1,q2..qr,где r-число степеней свободы {qα},α=1,2..r.Обоб. скорости { .Тогда ф.Лагранжа для мех. сис. с r степ. свободы L=L{qα, С помощью прин-ципа наименьшего принципа найдём уравнение движения S= δS=0 δS= = + =

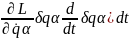Δqαdt=0 В рез.пол.

36.Определить собственные частоты колебания двойного математического маятника Будем рассматривать р-е ур-ийдв-я кол-ся мех-ой сис-мы в линприбл.,т.е когда будем строить ф-ю Лагранджа,то ф-ии будет реализовывать разложение слагаемых до 2ого порядка по оклон.обобщающихкоордин.от состояния устойчивого равновесия.Рассмотрим

L(ϕ,ψ,ϕ,ψ)Пусть механич.сис-ма имеет r степеней свободы.Этамеханич.сисмаопредел-сяобобщ.коорд. коорд-ми q_1,q_2….q_r..Обозначим q_r,где L=1,2….r,тогда L=L(q_λ,q_λ)=T-U(q_λ)

Будем рассматривать состо-я мех сис-мы,гдепотенц.энергия минимальна.X_λ=q_λ-q⁽⁰⁾_λ отклон.обобщ.коорд-тыот положения равновесия.U(q_λ)=U(q⁽⁰⁾_λ+x_λ)=U(q⁽⁰⁾_λ)+ + +….T= Ф-ю Лагранжа для колеб.многомернойсис-мы в лин.приближении можем записать в виде L=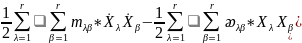 где координаты опред.пар-ми коэ-ты

37. Решить уравнения колебания длядвойного математ. маятникаБудем рассматривать р-е ур-ийдв-я кол-ся мех-ой сис-мы в линприбл.,т.е когда будем строить ф-ю Лагранджа,то ф-ии будет реализовывать разложение слагаемых до 2ого порядка по оклон.обобщающихкоордин.от состояния устойчивого равновесия

L(ϕ,ψ,ϕ,ψ)Пусть механич.сис-ма имеет r степеней свободы.Этамеханич.сисмаопредел-сяобобщ.коорд. коорд-ми q_1,q_2….q_r..Обозначим q_r,где L=1,2….r,тогда L=L(q_λ,q_λ)=T-U(q_λ)

Будем рассматривать состо-я мех сис-мы,гдепотенц.энергия минимальна.X_λ=q_λ-q⁽⁰⁾_λ отклон.обобщ.коорд-тыот положения равновесия.U(q_λ)=U(q⁽⁰⁾_λ+x_λ)=U(q⁽⁰⁾_λ)+ + +….

T= Ф-ю Лагранжа для колеб.многомернойсис-мы в лин.приближении можем записать в виде L= где координаты опред.пар-ми коэ-ты

33. определение собственных частот многомерн.колеб в лин.приблежении.Будем рассматривать р-е ур-ийдв-я кол-ся мех-ой сис-мы в линприбл.,т.е когда будем строить ф-ю Лагранджа,то ф-ии будет реализовывать разложение слагаемых до 2ого порядка по оклон.обобщающихкоордин.от состояния устойчивого равновесия

L(ϕ,ψ,ϕ,ψ)Пусть механич.сис-ма имеет r степеней свободы.Этамеханич.сисмаопредел-сяобобщ.коорд. коорд-ми q_1,q_2….q_r..Обозначим q_r,где L=1,2….r,тогда L=L(q_λ,q_λ)=T-U(q_λ)

Будем рассматривать состо-я мех сис-мы,гдепотенц.энергия минимальна.X_λ=q_λ-q⁽⁰⁾_λ отклон.обобщ.коорд-тыот положения равновесия.U(q_λ)=U(q⁽⁰⁾_λ+x_λ)=U(q⁽⁰⁾_λ)+ + +….

T= Ф-ю Лагранжа для колеб.многомернойсис-мы в лин.приближении можем записать в виде L= где координаты опред.пар-ми коэ-ты

в опрос 40