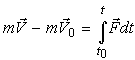13.Введение в динамику системы

Динамическая система представляет собой математическую модель некоторого объекта, процесса или явления.

Динамическая система также может быть представлена как система, обладающая состоянием. При таком подходе, динамическая система описывает (в целом) динамику некоторого процесса, а именно: процесс перехода системы из одного состояния в другое. Фазовое пространство системы — совокупность всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, по которому система переходит из начального состояние в другое.

Различают системы с дискретным временем и системы с непрерывным временем.

Динамическая система (как с дискретным, так и с непрерывным временем) является по существу синонимом автономной системы дифференциальных уравнений, заданной в некоторой области и удовлетворяющей там условиям теоремы существования и единственности решения дифференциального уравнения. Положениям равновесия динамической системы соответствуют особые точки дифференциального уравнения, а замкнутые фазовые кривые — его периодическим решениям.

Основное содержание теории динамических систем — это исследование кривых, определяемых дифференциальными уравнениями. Сюда входит разбиение фазового пространства на траектории и исследование предельного поведения этих траекторий: поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств (многообразий). Важнейшие понятие теории динамических систем — это устойчивость (способность системы сколь угодно долго оставаться около положения равновесия или на заданном многообразии) и грубость (сохранение свойств при малых изменениях структуры динамической системы).

Динамической системой, заданной на гладком многообразии  , называется отображение  , записываемое в параметрическом виде  , где  , которое является дифференцируемым отображением, причём   — тождественное отображение пространства  . В случае стационарных обратимых систем однопараметрическое семейство   образует группу преобразований топологического пространства  , а значит, в частности, для любых   выполняется тождество  .

Из дифференцируемости отображения   следует, что функция   является дифференцируемой функцией времени, её график расположен в расширенном фазовом пространстве   и называется интегральной траекторией (кривой) динамической системы. Его проекция на пространство  , которое в носит название фазового пространства, называется фазовой траекторией (кривой) динамической системы.

Задание стационарной динамической системы эквивалентно разбиению фазового пространства на фазовые траектории. Задание динамической системы в общем случае эквивалентно разбиению расширенного фазового пространства на интегральные траектории.

14.Теоремы об изменении количества движения.

Для доказательства теоремы запишем дифференциальное уравнение движения точки (основное уравнение динамики точки) в виде mdV / dt = F. Напомним, что здесь F - равнодействующая сил, приложенных к точке.

Внесем постоянную величину - m под знак производной и, разделяя переменные, получим математическую запись теоремы в дифференциальной форме:

d(mV) = Fdt

(1)

Произведение mV назовем количеством движения точки, произведение Fdt - элементарным импульсом силы (равнодействующей), что позволяет сформулировать теорему об изменении количества движения материальной точки в дифференциальной форме: дифференциал от количества движения материальной точки равен элементарному импульсу сил, приложенных к точке.

Количество движения материальной точки - это векторная мера движения точки. Направление вектора количества движения точки q совпадает с направлением вектора скорости V. Единицей количества движения является кг·м/с.

Элементарный импульс силы - это векторная мера действия силы, отражающая, что действие силы зависит не только от величины и направления силы, но и от продолжительности действия силы.

Предположим, что за промежуток времени от V₀ до V скорость точки изменилась от до , и при этих предположениях проинтегрируем (1). В результате получаем запись теоремы в интегральной форме:

(2)

Интеграл в правой части (2) назовем полным импульсом силы (равнодействующей) и сформулируем теорему об изменении количества движения материальной точки в интегральной форме: изменение количества движения материальной точки за некоторый промежуток времени равно полному импульсу сил, приложенных к точке. Заметим, что импульс силы измеряется в Н·м.

Проектируя выражения (1) и (2) на оси координат, можно получить запись теоремы в дифференциальной и интегральной формах в координатном виде, что предлагается сделать самостоятельно.

На практике теорема применяется, когда интеграл в правой части (2) можно взять, то есть когда F = F(t) или F = const.

Чаще всего теорема применяется для решения задач, когда F = 0 и имеет место закон сохранения количества движения материальной точки. В этом случае определенный интеграл в правой части (2) равен нулю и

mV = const = mV0

(3)

то есть при равенстве нулю равнодействующей сил, приложенных к материальной точке, ее количество движения остается постоянным, равным своему начальному значению.

Закон сохранения имеет место и при движении вдоль одной из осей, например Ox, когда F_x = 0. В этом случае mV_x = const = mV_0x.