9. Сложное движение твердого тела. Вращения.

Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все его точки, лежащие на некоторой прямой, называемой осью вращения, все время остаются неподвижными. Вращательное движение тела – такое движение твердого тела, при котором все точки, принадлежащие некоторой прямой, неизменно связанной с телом, остаются неподвижными. Эта прямая называется осью вращения тела. При этом движении все точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на оси вращения. Уравнение (закон) вращательного движения: j=f(t) – угол поворота тела в радианах. Угловая скорость: , [рад/с] – определяет быстроту изменения угла поворота. Вектор угловой скорости тела, совершающего вращение вокруг неподвижной оси, направлен вдоль оси вращения так, что если смотреть ему навстречу вращение будет против час. стрелке. "n"– число оборотов в мин. [об/мин], 1об=2p рад, . Угловое ускорение тела: , [рад/с2]. Вектор углового ускорения также направлен вдоль оси вращения. При ускоренном движении совпадает по направлению с угловой скоростью и противоположно при замедленном вращении. Частные случаи вращения тела: 1) Равномерное вращение: w=const, j=wt, w=j/t, 2) Равнопеременное вращение: w=w0+et; , здесь начальный угол j0=0. Скорости и ускорения точек вращающегося тела. – скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус–вектор этой точки. Модуль векторного произведения: v=w×r×sin(a)= w×(CM), (СМ) – расстояние от точки М до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону вращения.

10.Введение в динамику. Интегрирование дифференциальных уравнений.

Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил. В динамике при изучении движения тел принимают во внимание, как действующие силы, так и инертность самих материальных тел. Инертность и представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Количественной мерой инертности данного тела является физическая величина, называемая массой тела. В механике масса т рассматривается как величина скалярная, положительная и постоянная для каждого данного тела. В общем случае движение тела зависит не только от его суммарной массы и приложенных сил; характер движения может еще зависеть от формы тела, точнее от взаимного расположения образующих его частиц (т. е. от распределения масс). Материальной точкой называют материальное тело (тело, имеющее массу), размерами которого при изучении его движения можно пренебречь. Второй закон (основной закон динамики) гласит: произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы. Математически этот закон выражается векторным равенством . При этом между модулями ускорения и силы имеет место зависимость ma = F. Второй закон динамики имеет место только по отношению к инерциальной системе отсчета. Из этого закона непосредственно видно, что мерой инертности материальной точки является ее масса, так как две разные точки при действии одной и той же силы получают одинаковые ускорения только тогда, когда будут равны их массы. Если же массы будут разные, то точка, масса которой больше (т. е. более инертная), получит меньшее ускорение, и наоборот. Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе, т.е. равнодействующей , равной геометрической сумме этих сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид или .Основное уравнение динамики можно записать так 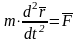или так 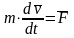Проецируя уравнение на оси координат получаем

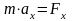
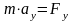
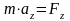
так как 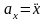, , 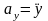, 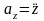то

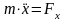
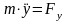
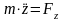
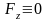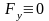Частные случаи: А) Точка движется в плоскости. Выбираем в плоскости координаты xOy получаем Б) Точка движется по прямой. Выбираем на прямой координату Ox получаем . Основное уравнение динамики можно спроецировать на естественные подвижные оси. , , , ,
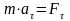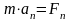
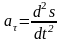
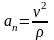