
§2. Определиетли.
Рассмотрим квадратную матрицу -ного порядка.
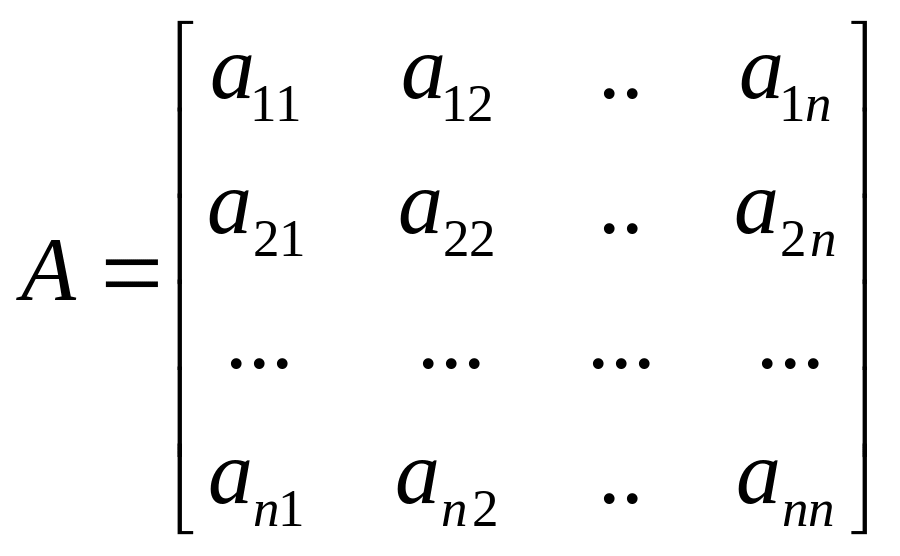 .
.
Каждой квадратной матрице может быть поставлена в соответствие некоторая числовая характеристика называемая определителем или детерминантом. Порядок определителя и матрицы совпадает (матрица – таблица, определитель - число).
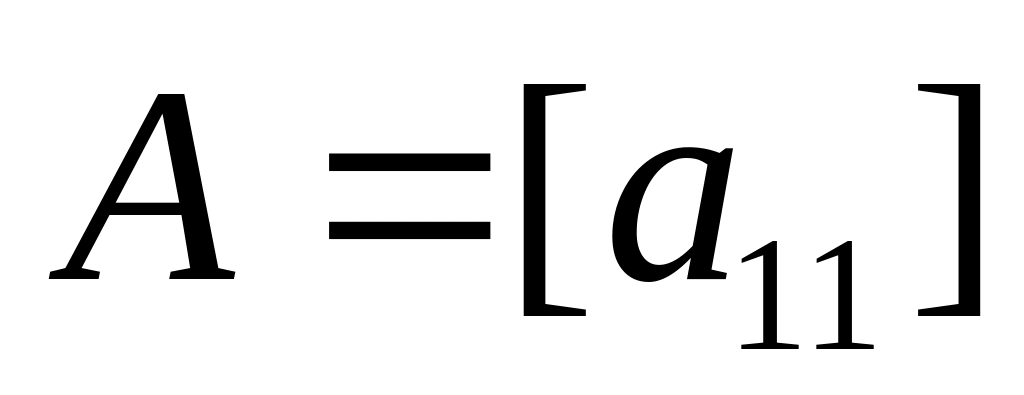 -
матрица первого порядка.
-
матрица первого порядка.
![]() .
.
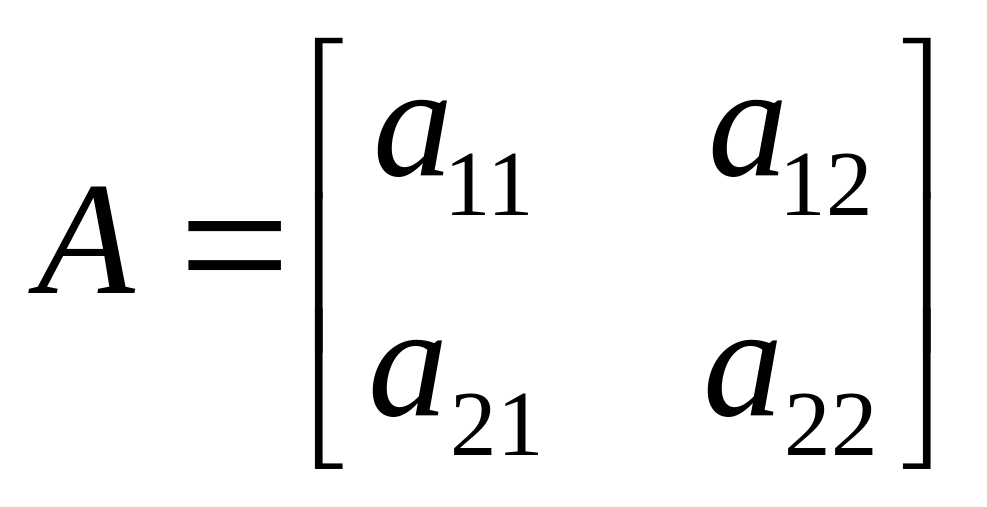 -
матрица второго порядка.
-
матрица второго порядка.
![]() .
.
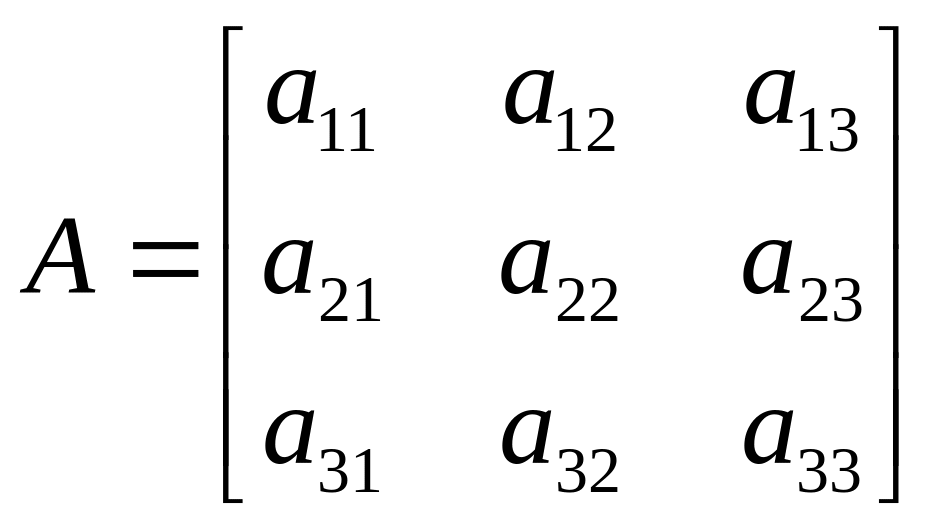 -
матрица третьего порядка.
-
матрица третьего порядка.
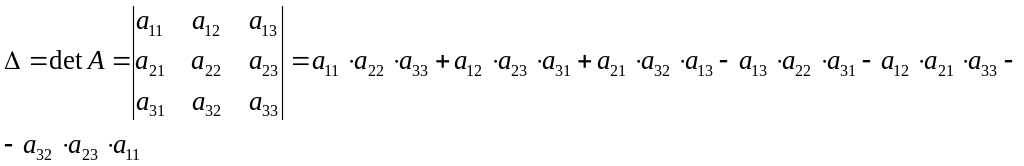
Правило треугольника:
Слагаемые “+”. Слагаемые “-”.
Минором данного элемента
 ,
называется определитель полученный
из данного определителя путем вычеркивания
строки и столбца на пересечении, которых
стоит данный элемент
.
,
называется определитель полученный
из данного определителя путем вычеркивания
строки и столбца на пересечении, которых
стоит данный элемент
.
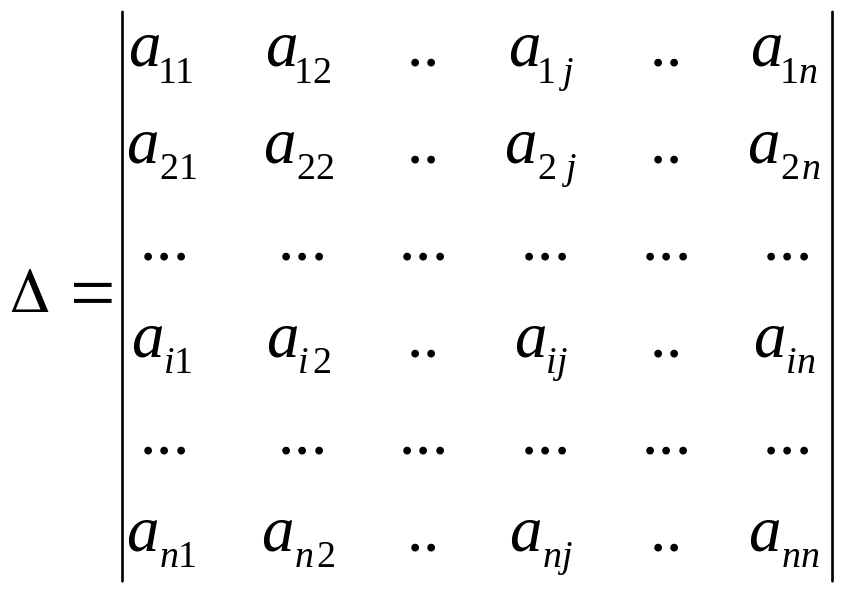
![]()
![]() определитель
определитель
![]() -
порядка.
-
порядка.
Алгебраическим
дополнением элемента
называется
его минор взятый со знаком
![]() (“+”
если
(“+”
если
![]() -
четное и “-”,
если
-
четное и “-”,
если
![]() -
не четное).
-
не четное).
![]() .
.
Определитель равен, сумме произведений элементов некоторой строки (или столбца) на их алгебраические дополнения.
![]() .
.
Это
правило универсально используется для
вычисления определителей
![]() порядка.
порядка.
Пример:
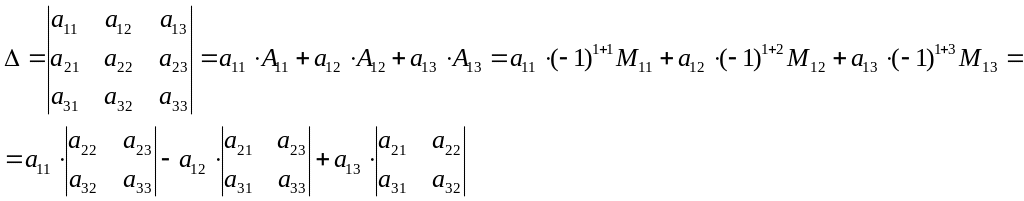
Свойства определителей:
10. Величина определителя не измениться при его транспонировании (то есть замене строк столбцами):
![]() .
.
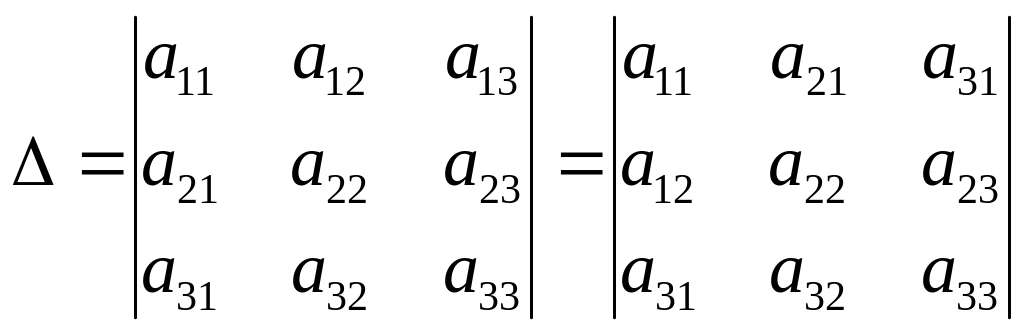 .
.
Это свойство равноправия строк и столбцов. Строки и столбцы носят общее название “рядов” определителя.
20. При перестановке двух параллельных рядов определителя знак определителя меняется на противоположный.
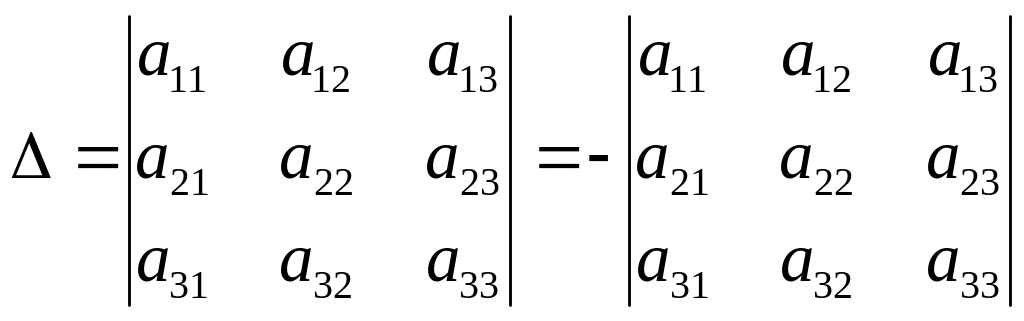 .
.
30. Определитель равен 0, если все элементы некоторого его ряда равны 0.
 .
.
40. Определитель, имеющий два одинаковых параллельных ряда равен 0.
50. Если элементы некоторого ряда определителя пропорциональны элементам параллельного ряда или равны линейной комбинации элементов параллельных рядов, то такой определитель равен 0.
60. Общий множитель элементов некоторого ряда можно вынести за знак определителя. И наоборот, чтобы умножить определитель на некоторое число достаточно умножить на это число элементы некоторого ряда.
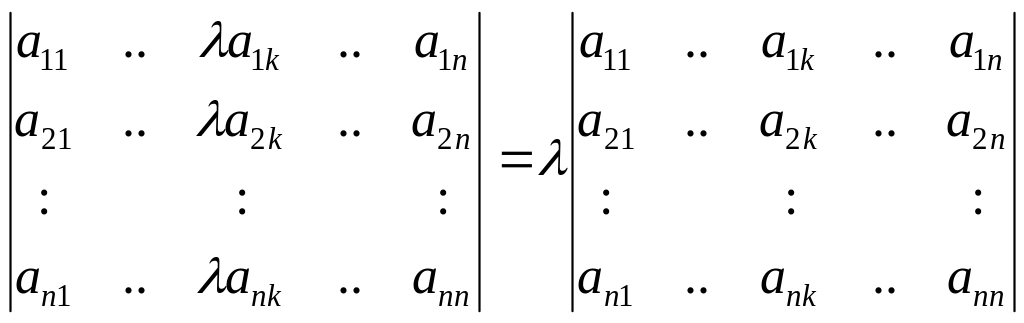 .
.
80. Величина определителя не изменится, если к элементам некоторого ряда определителя прибавить элементы параллельного ряда умноженные на некоторое число.
??????????????????????????????.
90. Сумма произведений элементов некоторого ряда на алгебраические дополнения параллельного ряда равно 0. Умножим элементы первого ряда на алгебраические дополнения второго ряда.
 .
.
По формуле (1) определитель
равен сумме произведений элементов
некоторого ряда на их алгебраические
дополнения. Таким образом элементы
![]() можно записать вместо элементов второй
строки. Получившийся определитель по
свойству 40 равен 0.
можно записать вместо элементов второй
строки. Получившийся определитель по
свойству 40 равен 0.
100. Если и - квадратные матрицы одинаковой размерности, то
![]() .
.
110. Определители диагональной и треугольной матриц равен произведению элементов стоящих на их главных диагоналях:
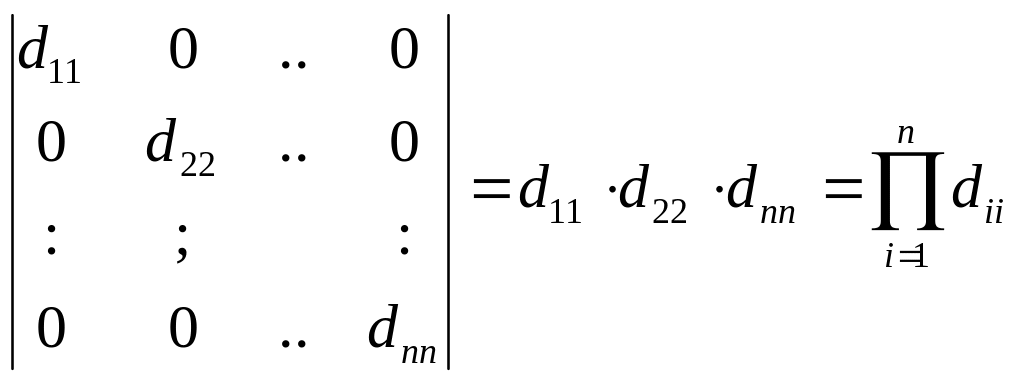 .
.
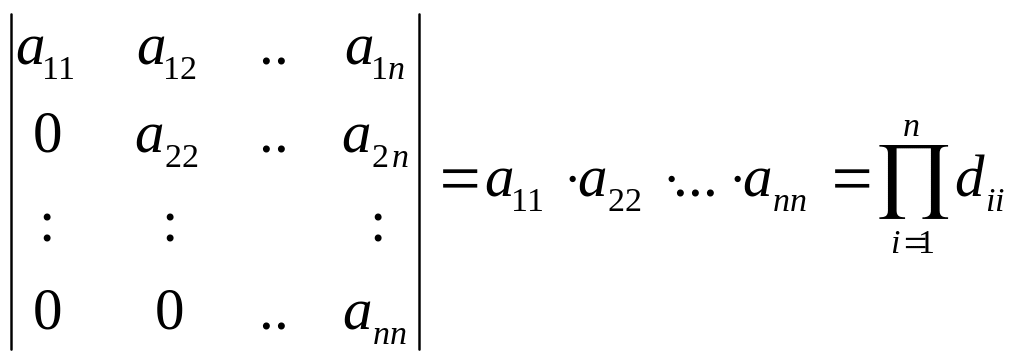 .
.
В справедливости всех перечисленных свойств можно убедиться непосредственным вычислением определителей.
§3. Обратная матрица.
Понятие обратных
матриц вводится для матриц только строго
квадратных. Рассмотрим квадратную
матрицу
![]() порядка. Матрица
называется не вырожденной (не особенной),
если ее определитель
порядка. Матрица
называется не вырожденной (не особенной),
если ее определитель
![]() отличен от нуля.
отличен от нуля.
Матрица
![]() является обратной матрицей для матрицы
, если выполняется условие:
является обратной матрицей для матрицы
, если выполняется условие:
![]() .
.
Теорема: Чтобы для квадратной матрицы существовала обратная матрица , необходимо и достаточно, чтобы матрица была не врожденной.
Доказательство:
Необходимость.
Пусть существует, то есть .
![]() /
по свойству
определителей 100./
/
по свойству
определителей 100./![]()
![]() .
(*)
.
(*)
Из (*) следует, что
![]() ,
то есть
-
не вырожденная.
,
то есть
-
не вырожденная.
Достаточность.
Пусть матрица не вырожденная, то есть . Покажем, что существует .
Доказательство проведем для случая квадратной матрицы третьего порядка.
![]() .
.
10. Построить матрицу элементами которой являются алгебраические дополнения соответствующих элементов матрицы .
 .
.
20. Транспонируем матрицу .

30. Умножим
![]() на число
на число
![]() .
.
![]() (**)
(**)
Покажем, что матрица (**) является обратной по отношению к матрице .
По
![]() :
:
Перемножим и .
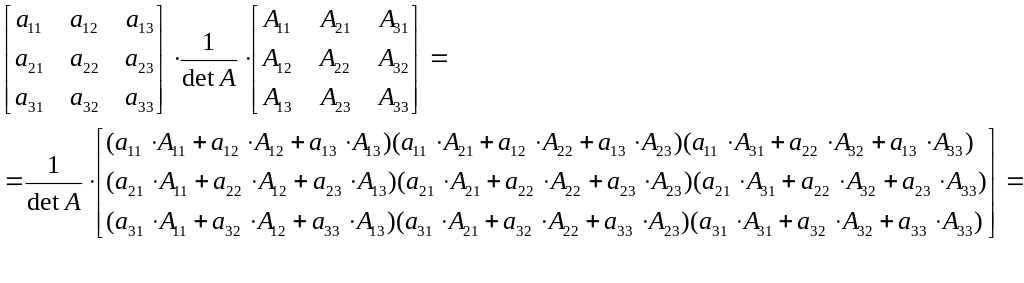
=/ получаем
![]() по
формуле (1)0 по свойству 90./
по
формуле (1)0 по свойству 90./
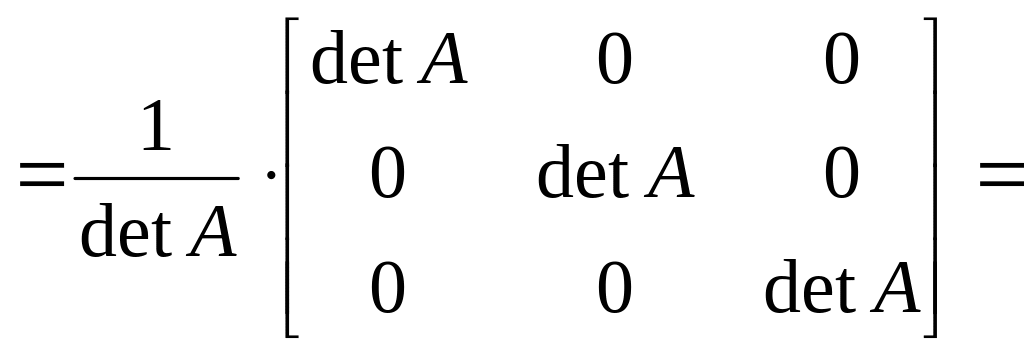
=/ по
свойству умножения матриц на число,
получаем/
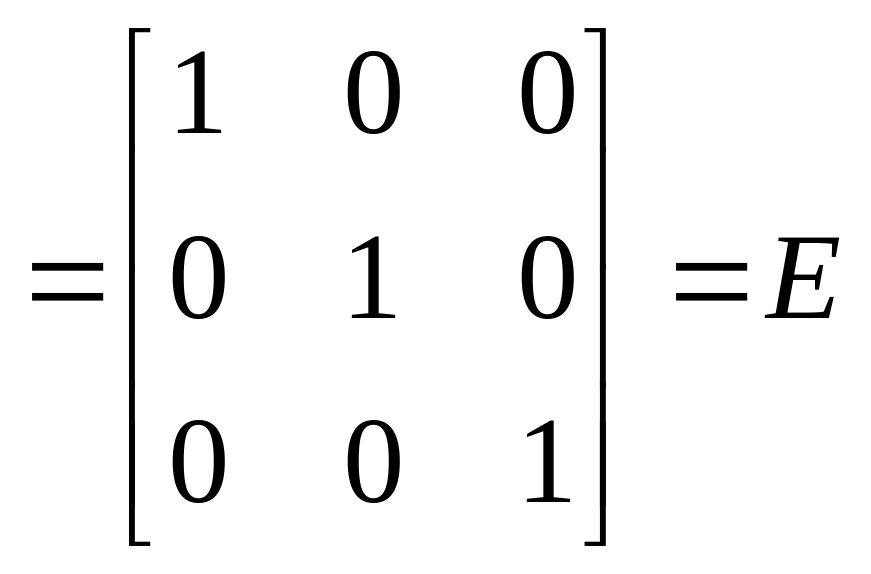 .
.
Аналогично, можно
показать, что
![]() .
.
Правило нахождения обратной матрицы:
10. Убедиться, что не вырожденная, то есть сосчитать .
20. Составить матрицу из алгебраических дополнений к элементам матрицы .
30. Транспонировать полученную матрицу.
40. Транспонированную
матрицу умножить на
![]() .
.
50. Проверка правильности вычислений:
![]()

![]()
Матрица состоящая из
алгебраических дополнений к матрице
называется присоединенной к матрице
и обозначается
![]() .
.
![]() (2)
(2)
Свойства обратной матрицы:
10.
![]() ,
если существуют
и
,
если существуют
и
![]() .
.
20.
![]() .
.
30.
![]()
40.
![]() .
.
50. Если
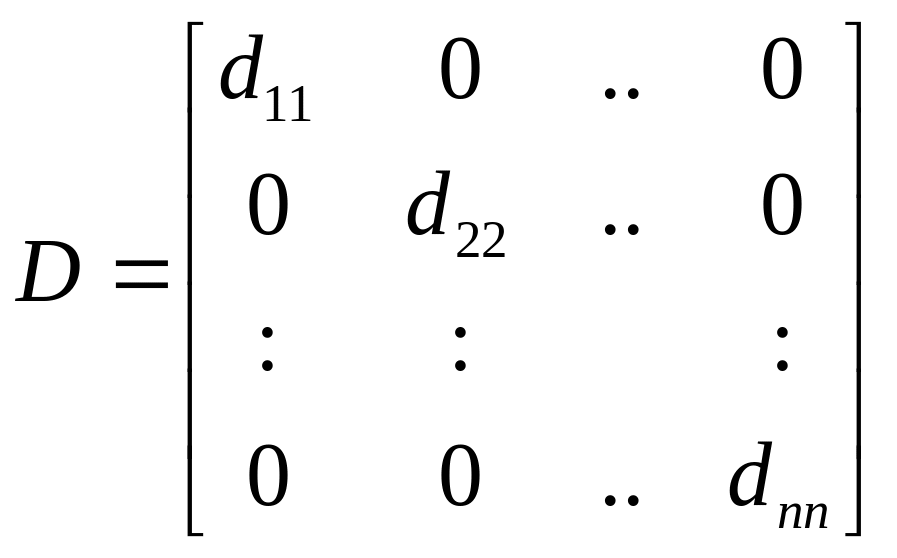 ,
то
,
то
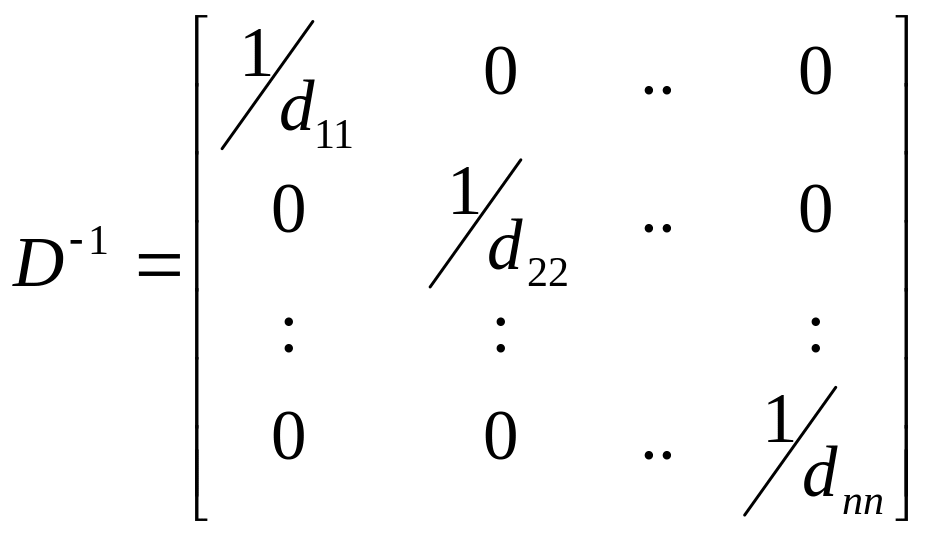 .
.
Решение линейных матричных уравнений:
10.
![]()
Умножим обе части уравнения на матрицу слева:
![]()
![]()
![]()
![]() .
.
20.
![]()
Уравнение умножаем
на
![]() справа:
справа:
![]()
![]()
![]()
30.
![]()
Умножаем обе части
уравнения: слева на
,
справа на
![]() .
.
![]()
![]() .
.
